博客

二叉树

是什么?

二叉树就是每个节点(Node)最多只有


两个子节点


的树结构,且子树有

左右之分

,不能任意颠倒顺序.

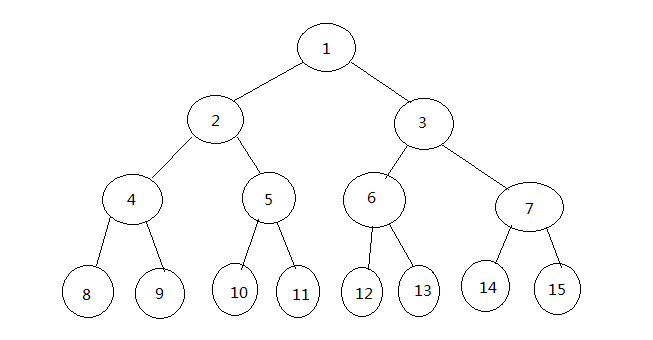
根据二叉树的特性,便有了



二叉排序树



. 一般数据以二叉树作为数据结构储存时,都是按照二叉排序树的一般规则(“小放左,大放右”).

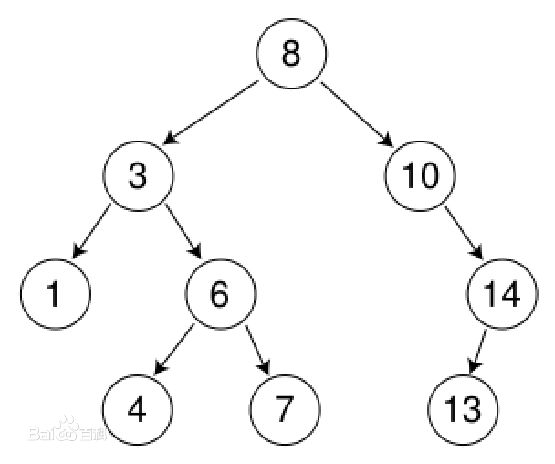
为了各位检验,main()函数和测试数据在最后给出.

二叉树节点定义

struct Node {
    int val;
    Node *lson, *rson;
    Node(int v=0, Node *ls=NULL, Node *rs=NULL): val(v), lson(ls), rson(rs) {};
};

二叉排序树创建

void read(int s[], int st, int ed) {
    queue<int> tmp;
    for(int i=st; i<ed; ++i) tmp.push(s[i]);
    swap(tmp, buf);
}

bool build() {
    while(!buf.empty()) {
        if(!insert(root, buf.front())) return false;
        buf.pop();
    }
    return true;
}

bool insert(Node *(&x), int v) {
    if(x == NULL) {
        x = new (std::nothrow) Node(v, NULL, NULL);
        if(x == NULL) return false;
    } else {
        if(v < x->val) {
            return insert(x->lson, v);
        } else if(v == x->val) {
            /* 按需调整 */
//                return insert(x->lson, v);
//                return insert(x->rson, v);
            return true;
        } else {
            return insert(x->rson, v);
        }
    }
    return true;
}

写了这么个建树函数后,一定是需要检验的了,而检验的方法,一般就是列出四个遍历方式(先序,中序,后序,按层),判断是否正确咯.

这里给出各种遍历的代码.

先序遍历

void _pre_tra(Node *x) {
    if(x) {
        cout << x->val << " ";
        _pre_tra(x->lson);
        _pre_tra(x->rson);
    }
}

void preorder_traversal() {
    _pre_tra(root);
    cout << endl;
}

中序遍历(一般可认作从小到大输出)

void _in_tra(Node *x) {
    if(x) {
        _in_tra(x->lson);
        cout << x->val << " ";
        _in_tra(x->rson);
    }
}

void inorder_traversal() {
    _in_tra(root);
    cout << endl;
}

后序遍历

void _post_tra(Node *x) {
    if(x) {
        _post_tra(x->lson);
        _post_tra(x->rson);
        cout << x->val << " ";
    }
}

void postorder_traversal() {
    _post_tra(root);
    cout << endl;
}

按层遍历      (我认为思想与bfs(宽度搜索)完全一样). 按层遍历十分重要,下面几种二叉树相关的算法我都是用次实现的.

void level_traversal() {
    queue<Node*> que;
    if(root == NULL) return;
    que.push(root);
    while(!que.empty()) {
        Node *cur = que.front();
        que.pop();
        
        cout << cur->val << " ";
        if(cur->lson) que.push(cur->lson);
        if(cur->rson) que.push(cur->rson);
    }
    cout << endl;
}

分割线

二叉排序树类实现

class BSTree {
private:
    struct Node {
        int val;
        Node *lson, *rson;
        Node(int v=0, Node *ls=NULL, Node *rs=NULL): val(v), lson(ls), rson(rs) {};
    };
    
    Node *root;
    queue<int> buf;

    void _pre_tra(Node *x) {
        if(x) {
            cout << x->val << " ";
            _pre_tra(x->lson);
            _pre_tra(x->rson);
        }
    }
    
    void _in_tra(Node *x) {
        if(x) {
            _in_tra(x->lson);
            cout << x->val << " ";
            _in_tra(x->rson);
        }
    }
    
    void _post_tra(Node *x) {
        if(x) {
            _post_tra(x->lson);
            _post_tra(x->rson);
            cout << x->val << " ";
        }
    }
    
public:
    BSTree() {
        root = NULL;
    }
    
    ~BSTree() {
        clear();
    }
    
    void clear() {
        queue<int> tmp;
        swap(buf, tmp);
        queue<Node*> que;
        if(root == NULL) return;
        que.push(root);
        while(!que.empty()) {
            Node *cur = que.front();
            que.pop();
            if(cur->lson) que.push(cur->lson);
            if(cur->rson) que.push(cur->rson);
            delete cur;
        }
        root = NULL;
    }
    
    void read(int s[], int st, int ed) {
        queue<int> tmp;
        for(int i=st; i<ed; ++i) tmp.push(s[i]);
        swap(tmp, buf);
    }
    
    bool build() {
        while(!buf.empty()) {
            if(!insert(root, buf.front())) return false;
            buf.pop();
        }
        return true;
    }
    
    bool insert(Node *(&x), int v) {
        if(x == NULL) {
            x = new (std::nothrow) Node(v, NULL, NULL);
            if(x == NULL) return false;
        } else {
            if(v < x->val) {
                return insert(x->lson, v);
            } else if(v == x->val) {
                /* 按需调整 */
//                return insert(x->lson, v);
//                return insert(x->rson, v);
                return true;
            } else {
                return insert(x->rson, v);
            }
        }
        return true;
    }

    void preorder_traversal() {
        _pre_tra(root);
        cout << endl;
    }
    
    void inorder_traversal() {
        _in_tra(root);
        cout << endl;
    }
    
    void postorder_traversal() {
        _post_tra(root);
        cout << endl;
    }
    
    void level_traversal() {
        queue<Node*> que;
        if(root == NULL) return;
        que.push(root);
        while(!que.empty()) {
            Node *cur = que.front();
            que.pop();
            
            cout << cur->val << " ";
            if(cur->lson) que.push(cur->lson);
            if(cur->rson) que.push(cur->rson);
        }
        cout << endl;
    }
};

使用样例：

8
23 45 12 6 7 89 13 47

#include <iostream>
#include <queue>
using namespace std;

/*
二叉排序树类定义
*/

int s[MAXN];
BSTree bst;

int main() {
    int n;
    while(cin >> n) {
        for(int i=0; i<n; ++i) cin >> s[i];
        bst.read(s, 0, n);
        bst.build();
        bst.preorder_traversal();
        bst.inorder_traversal();
        bst.postorder_traversal();
        bst.level_traversal();
        bst.clear();
        break;
    }
    return 0;
}