博客

这种运算有点理解，反正我是觉得有点绕，所以单独拿出来，表示注重。

在这种运算中，x(n)的每个样本都要移位一个量k得到一个移位的序列y(n).

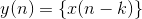
如果令m=n-k，那么n = m + k，上面运算给出为：

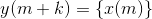
这就是说，把m当成x的自变量，那么y的自变量n就等于m + k，对于n而言，相当于x右移了k位。

响应的函数可以定义如下：

function [y,n] = sigshift(x,m,k)

%implements y(n) = x(n – k)

%_________________________

%[y,n] = sigshift(x,m,k)

%

n = m+k;

y = x;

下面我们验证下这个函数是否实现移位功能：

clc

clear

close all

n = 0:5;

x = randn(1,6);

subplot(2,1,1)

stem(n,x);

xlabel(‘n’);ylabel(‘x(n)’);

[y,n]=sigshift(x,n,4);

subplot(2,1,2)

stem(n,y);

xlabel(‘n’);ylabel(‘y(n) = x(n -4)’);

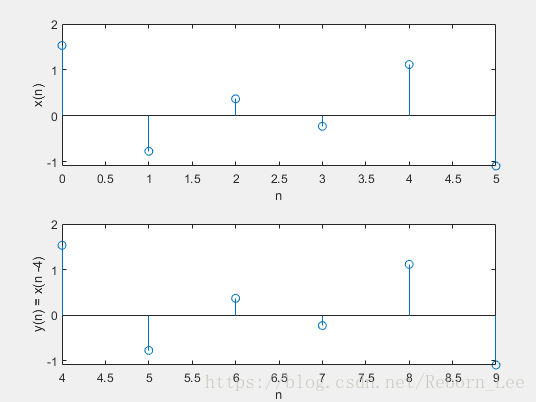
可见，实现了移位运算。

推荐一首歌：违章动物

本文同步分享在 博客“李锐博恩”(CSDN)。

如有侵权，请联系 support@oschina.cn 删除。

本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。