博客

给定一个二叉搜索树的根节点

root

，和一个整数

k

，请你设计一个算法查找其中第

k



个最小元素（从 1 开始计数）。

示例 1：

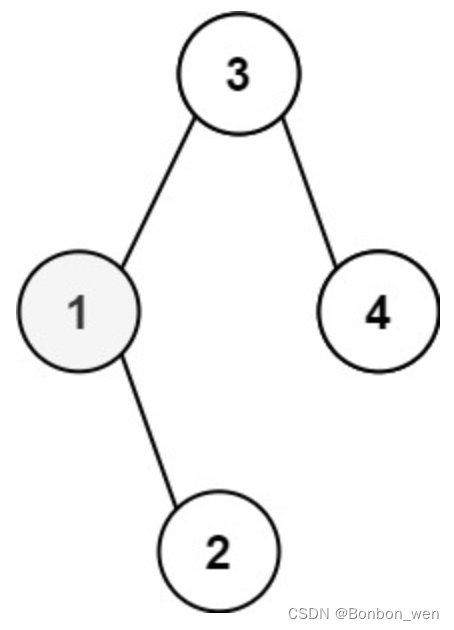
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

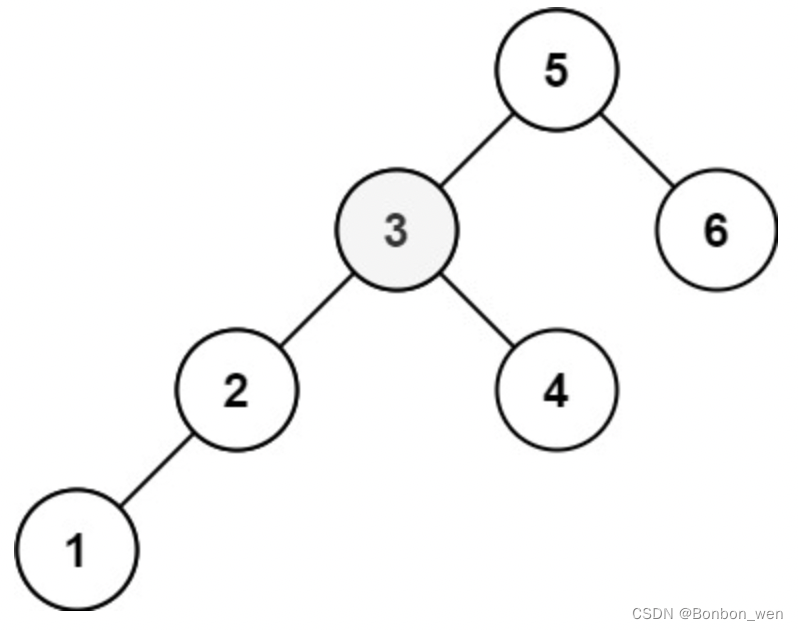
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

• 树中的节点数为
  
n

  。
• 
1 <= k <= n <= 104

• 
0 <= Node.val <= 104


来源：力扣（LeetCode）

链接：

https://leetcode.cn/problems/kth-smallest-element-in-a-bst/


著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

感谢官方题解，传送门

二叉搜索树中第K小的元素

class Solution {
	private int res = 0;
	private int rank = 0;

    public int kthSmallest(TreeNode root, int k) {
//		return kthSmallestI(root, k);
//		return kthSmallestII(root, k);
		MyBST my = new MyBST(root);
		return my.kthSmallest(k);
	}

	//方法三：如果你需要频繁地查找第 k 小的值，你将如何优化算法？
	//重新定义BST树，增加字段记录以该节点为根节点的树的节点总数
	class MyBST{
		TreeNode root;
		Map<TreeNode, Integer> nodeNum;

		public MyBST(TreeNode root) {
			this.root = root;
			this.nodeNum = new HashMap<>();
			countNodeNum(root);
		}

		public int kthSmallest(int k) {
			while (root != null) {
				int left = getNodeNum(root.left);
				if (k < left + 1) {
					root = root.left;
				} else if (k > left + 1) {
					root = root.right;
					k -= left + 1;
				} else {
					break;
				}
			}
			return root.val;
		}

		private int getNodeNum(TreeNode node) {
			return nodeNum.getOrDefault(node, 0);
		}

		private int countNodeNum(TreeNode root) {
			if (root == null) {
				return 0;
			}
			int num = 1 + countNodeNum(root.left) + countNodeNum(root.right);
			nodeNum.put(root, num);
			return num;
		}
	}
	//方法二：利用栈中序遍历
	//时间复杂度：O(H+k)，空间复杂度O(H)
	private int kthSmallestII(TreeNode root, int k) {
		if (root == null) {
			return 0;
		}
		Stack<TreeNode> stack = new Stack<>();
		while (!stack.isEmpty() || root != null) {
			while (root != null) {
				stack.push(root);
				root = root.left;
			}
			root = stack.pop();
			if (--k == 0) {
				break;
			}
			root = root.right;
		}
		return root.val;
	}

	//方法一：BST中序遍历默认有序（升序），时间和空间复杂度O(N)
	private int kthSmallestI(TreeNode root, int k) {
		if (root == null) {
			return 0;
		}
		traverse(root, k);
		return res;
	}

	private void traverse(TreeNode root, int k) {
		if (root == null) {
			return;
		}
		traverse(root.left, k);
		rank++;
		if (k == rank) {
			res = root.val;
			return;
		}
		traverse(root.right, k);
	}
}