之前在看哈工大的编译原理mooc(第四次开课),发现他们的算法比通用的Thompson算法好用的多:
(以下图中哈工大误写成中科大)
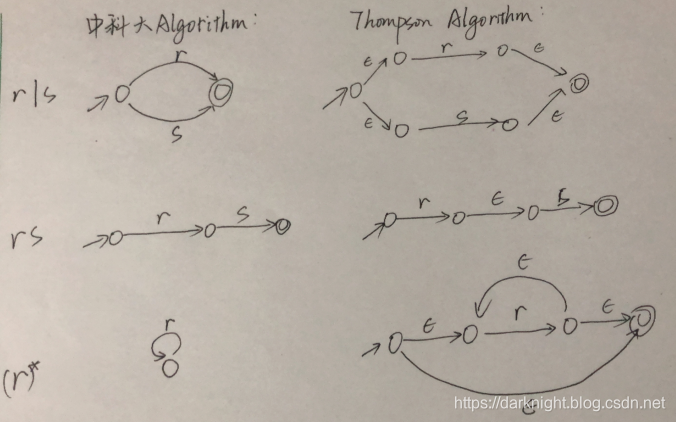
这两者的差异究竟能大到何种差异呢?如下图:

解决同一个RE,thompson算法转出来的NFA状态数足足多了15个!
这转DFA的时候谁顶得住啊!
经过多次实验,我发现使用哈工大算法的时候,转出来的DFA直接是状态数最小的,甚至不用Minimize状态数,这一度让我想证明出来这个算法转出来的NFA经过子集构造算法做出来的DFA状态数已经是最小的,
然后发篇paper。
但是转念一想,之所以thompson算法构造出来的NFA经过子集构造算法构造出来的DFA状态数不是最小,就是因为NFA中存在着大量的空边,那如果RE本身就存在着大量的空边,利用哈工大算法做出来的NFA转成DFA状态数也不可能是最小的,
到手的paper飞了。
但是为什么所有的书本以及学校的老师讲的都是thompson算法而不是哈工大算法呢?明明哈工大算法很好用啊!
终于有一天,骑小龟上课的路上,终于想到,如果最开始的图中,r和s代表的是一个长度不为1的字符串,那么哈工大的算法是不可行的。
比如(ab)*,用哈工大的算法就是没法画出NFA的。也就是说,大多数情况下,只有在r和s只表示一个字符的时候,用哈工大算法才能转。
虽然有这个局限性,但是我又有了新的想法,thompson算法里,哪些
ϵ
\epsilon
ϵ
边是可以不加的呢?
最后,结合陈鄞老师的回复,我得出了最简通用做题版jt Algorithm:

做题的时候,只要先用哈工大算法过一遍RE,如果发现转不了的部分,就用我的算法中对应的部分去替换相应部分即可,其他部分依然可以沿用哈工大算法,即可以混搭。
最后再说一说我对thompson算法中存在这么多多余空边的理解。
其实也很难说的出来,这是一种感受。多了这些空边,RE转DFA的递归定义就是完整的。不同的RE部分之间使用
ϵ
\epsilon
ϵ
去连接,使得RE部分和部分之间泾渭分明,多了一份从容不迫的优雅,
更多了十份题目的复杂度。
最后希望这学期cp可以满绩~
最后拿了4.5,有点可惜,考试居然让写yacc代码,跪了。