前言

在复现PoinNetGPD以及整个抓取系统的搭建，需要将仿真环境中Kinect_2得到的点云从相机坐标系/kinect2_ir_optical_frame转到世界坐标系中/world。由于是在gazebo中搭建的仿真环境，所以相机和world/base_link之间的tf变换是已知的。记录如下：

一、TF获得坐标系转换关系

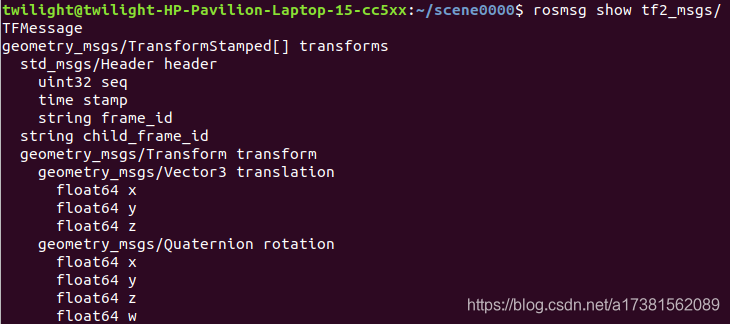
首先通过tf获得trans和quat。指以/world为参考系，从/world到/kinect2_ir_optical_frame需要的平移向量trans与旋转四元数quat。


注

：得到的quat是xyzw的顺序，一般我们使用的是wxyz（用作转欧拉角等操作）。

   listener = tf.TransformListener()
    get_transform = False
    while not get_transform:
        try:
            trans, quat = listener.lookupTransform('/world', '/kinect2_ir_optical_frame', rospy.Time(0))
            # print(trans, quat) ## quat xyzw
            # [0.8420404691331246, -0.04343000000000001, 1.5380334678129328], 
            # [-0.7071067251356604, 0.7071067247627317, -0.00028154403091668057, 0.00028248221651117067] xyzw
            # 转为wxyz形式
            quat_wxyz[0] = quat[3]
			quat_wxyz[1] = quat[0]
			quat_wxyz[2] = quat[1]
			quat_wxyz[3] = quat[2]

二、点云坐标系转换

这里我所使用的点云为Numpy格式，shape为（500，3）。转换的思路为 P’ = R×P+T，因为点云P相对为行向量，所以实际为P’=P×R+T（这里我理解的是，平时我们处理点旋转时，点一般为列向量，所以旋转矩阵左乘R×P，但这里为行向量，所以右乘）

1.将四元数转换为旋转矩阵

def quat2rot(quat_):
	q = quat_
	n = np.dot(q, q)
	if n < np.finfo(q.dtype).eps:
		return np.identity(3)
	q = q * np.sqrt(2.0 / n)
	q = np.outer(q, q)
	rot_matrix = np.array(
	[[1.0 - q[2, 2] - q[3, 3], q[1, 2] + q[3, 0], q[1, 3] - q[2, 0]],
	 [q[1, 2] - q[3, 0], 1.0 - q[1, 1] - q[3, 3], q[2, 3] + q[1, 0]],
	 [q[1, 3] + q[2, 0], q[2, 3] - q[1, 0], 1.0 - q[1, 1] - q[2, 2]]],
	dtype=q.dtype)

	return rot_matrix
	# [[ 1.05656190e-09 -1.00000000e+00 -1.32679448e-06]
    # [-9.99999682e-01  1.76031933e-12 -7.97653505e-04]
    # [ 7.97653505e-04  1.32679490e-06 -9.99999682e-01]]

2.点云变换

points_ = np.dot(points_, rotation_matrix) + np.array(cam_wor)

三、实验结果

下图为仿真kinect2相机发布的点云数据，是以/kinect2_ir_optical_frame为参考坐标系的



在python中订阅该topic得到点云并转为numpy后，将其坐标系转为世界坐标系，然后将numpy转为点云PointCloud2形式，以/world为参考坐标系发布



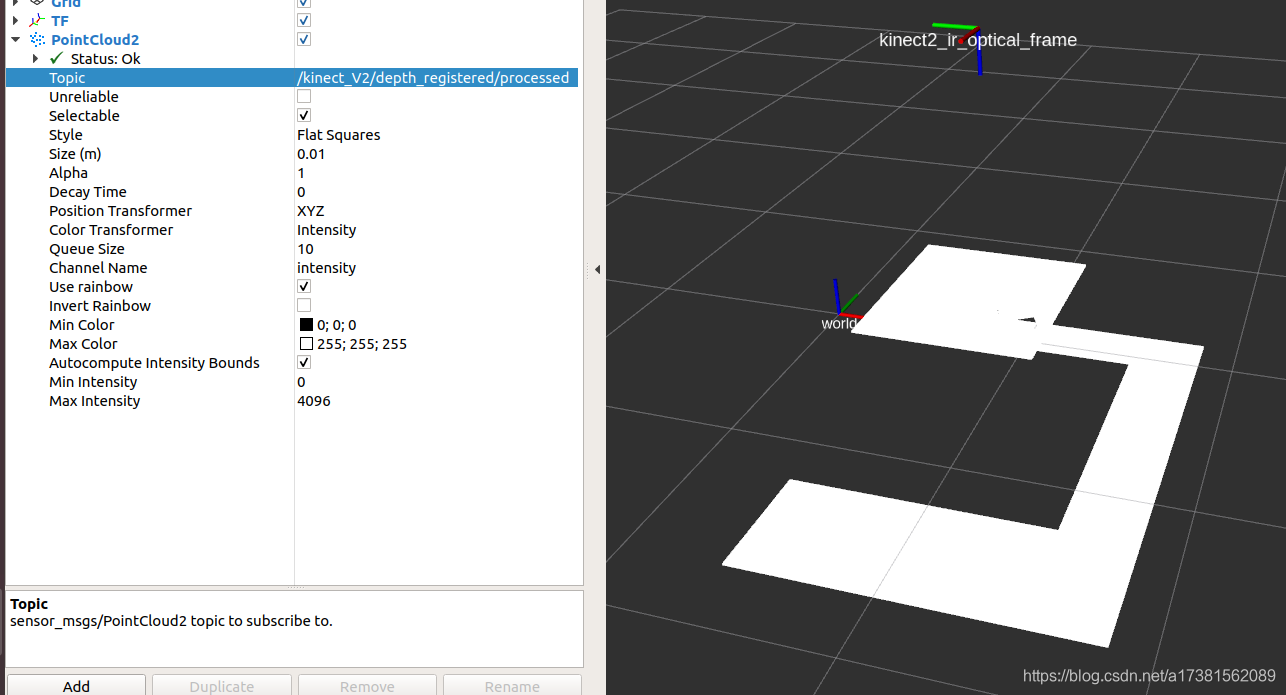
可以看出二者没有差别，证明上述过程正确。

总结

没啥好总结的，比较坑的就是lookuptransform得到的quaternion是xyzw的形式，需要转换一下。

之后还要部署真实机械臂（珞石工业机械臂），希望能够好好学一些东西。