1、简介
立体匹配的目的是为左图中的每一个像素点在右图中找到其对应点,这样就可以计算出视差:
d
i
s
p
a
r
i
t
y
=
x
i
−
x
j
disparity = x_i – x_j
d
i
s
p
a
r
i
t
y
=
x
i
−
x
j
(
x
i
x_i
x
i
和
x
j
x_j
x
j
分别表示两个对应点在图像中的列坐标)。
大部分立体匹配算法的计算过程可以分成以下几个阶段:匹配代价计算、代价聚合、视差计算、视差优化。
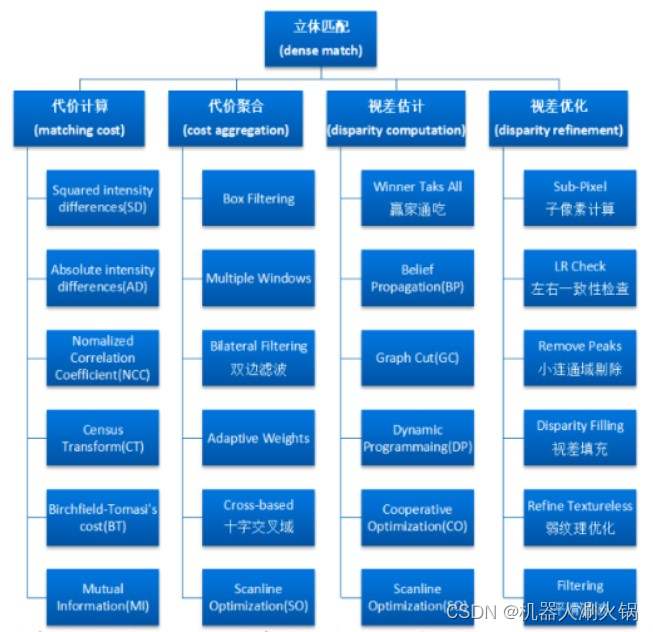
立体匹配是立体视觉中一个很难的部分,主要困难在于:
- 图像中可能存在重复纹理和弱纹理,这些区域很难匹配正确;
- 由于左右相机的拍摄位置不同,图像中几乎必然存在遮挡区域,在遮挡区域,左图中有一些像素点在右图中并没有对应的点,反之亦然;
- 左右相机所接收的光照情况不同;
- 过度曝光区域难以匹配;
- 倾斜表面、弯曲表面、非朗伯体表面;
- 较高的图像噪声等。
立体匹配的方法主要分两种,全局法和局部法
- 局部法主要有:BM、SGM、ELAS、Patch Match等。
- 全局法主要有:Dynamic Programming、Graph Cut、Belief Propagation等。
局部方法计算量小,匹配质量相对较低,全局方法省略了代价聚合而采用了优化能量函数的方法,匹配质量较高,但是计算量也比较大。由于全局法速度太慢,因此在实际应用中基本都是局部法。
目前OpenCV中已经实现的方法有BM、binaryBM、SGBM、binarySGBM、BM(cuda)、Bellief Propogation(cuda)、Constant Space Bellief Propogation(cuda)这几种方法。比较好用的是SGBM算法,它的核心是基于SGM算法,但和SGM算法又有一些不同,比如匹配代价部分用的是BT代价(原图+梯度图)而不是HMI代价等等。
2、匹配代价计算
匹配代价计算主要目的是计算左右双目图像像素之间的相关性,以此来相互匹配左右双目的像素点。最简单的方法就是直接计算两个点像素值的差异,但是因为只从一个点考虑,往往容易受到噪声的影响,于是有优化方法是将点换成window,计算其中的点的像素差值之和。但是这种基于像素值的算法,会对光线和畸变十分敏感,产生一定误差。于是还有一些是不基于像素值的算法,如census算法和Rank变换等。
2.1 AD
AD算法可以说是匹配代价计算中最简单的算法之一,其主要思想是不断比较左右相机中两点的灰度值大小,首先固定左相机中的一点,然后遍历右相机中的点,不断比较它们之前的灰度之差,灰度之差即为匹配代价。其数学公式为:
C
A
D
(
p
,
q
)
=
∣
I
L
(
p
)
−
I
R
(
q
)
∣
C_{AD}(p,q) = |I_L(p) – I_R(q)|
C
A
D
(
p
,
q
)
=
∣
I
L
(
p
)
−
I
R
(
q
)
∣
其中,
p
p
p
,
q
q
q
分别为左右图像中的两点,
I
L
(
)
I_L()
I
L
(
)
表示左图像中的灰度值,同理
I
R
(
)
I_R()
I
R
(
)
表示右图像中的灰度值。上式为灰度图像的匹配代价;若为彩色图像,则AD算法计算代价的公式为:
C
A
D
(
p
,
q
)
=
1
3
∑
i
=
R
,
G
,
B
∣
I
i
L
(
p
)
−
I
i
R
(
q
)
∣
C_{AD}(p,q) = {1 \over 3}\sum_{i=R,G,B} |I_{i}^{L}(p) – I_{i}^{R}(q)|
C
A
D
(
p
,
q
)
=
3
1
i
=
R
,
G
,
B
∑
∣
I
i
L
(
p
)
−
I
i
R
(
q
)
∣
即左右视图像素点的三个颜色分量之差的绝对值取平均。
AD算法是基于单个像素点计算的匹配代价,受光照不均、图像噪声影响较大,但对纹理丰富区域有较好的匹配效果。
2.2 SAD
SAD(Sum of absolute differences)也是匹配代价计算中基础的算法,其基本思想是:差的绝对值之和。相对于AD算法计算的代价是通过两点之间的灰度值进行的,而SAD的匹配代价则是通过某点及其一定范围内的像素点决定的,其基本流程如下:
首先输入两幅图像,一幅Left-Image,一幅Right-Image。其次对左图,依次扫描,选定一个锚点:
(1)构造一个小窗口,类似于卷积核;
(2)用窗口覆盖左边的图像,选择出窗口覆盖区域内的所有像素点;
(3)同样用窗口覆盖右边的图像并选择出覆盖区域的像素点;
(4)左边覆盖区域减去右边覆盖区域,并求出所有像素点灰度差的绝对值之和;
(5)移动右边图像的窗口,重复(3)-(4)的处理(这里有个搜索范围,超过这个范围跳出);
(6)找到这个范围内SAD值最小的窗口,即找到了左图锚点的最佳匹配的像素块。
其中,SAD的匹配代价计算公式如下:
C
S
A
D
(
p
,
q
)
=
∑
m
∈
N
p
,
n
∈
N
q
∣
I
L
(
m
)
−
I
R
(
n
)
∣
C_{SAD}(p,q) = \sum_{m∈N_p,n∈N_q} |I_L(m) – I_R(n)|
C
S
A
D
(
p
,
q
)
=
m
∈
N
p
,
n
∈
N
q
∑
∣
I
L
(
m
)
−
I
R
(
n
)
∣
其中 ,
N
p
N_p
N
p
、
N
q
N_q
N
q
分别表示
p
p
p
、
q
q
q
周围的像素点。
2.3 Cencus
Census变换法也被广泛用于匹配代价计算。它能够较好地检测出图像中的局部结构特征,如边缘、角点特征等。其基本的思想如下:在图像区域定义一个矩形窗口,用这个矩形窗口遍历整幅图像。选取中心像素作为参考像素,将矩形窗口中每个像素的灰度值与参考像素的灰度值进行比较,灰度值小于或等于参考值的像素标记为0,大于参考值的像素标记为1,最后再将它们按位连接,得到变换后的结果,变换后的结果是由0和1组成的二进制码流。
Cencus变换过程可通过如下公式表达:
T
(
p
)
=
⊗
q
∈
N
p
ξ
(
I
(
p
)
,
I
(
q
)
)
T(p) = ⊗_{q∈N_p} ξ(I(p), I(q))
T
(
p
)
=
⊗
q
∈
N
p
ξ
(
I
(
p
)
,
I
(
q
))
其中p是窗口中心像素,
q
q
q
是窗口中心像素以外的其他像素,
N
p
N_p
N
p
表示中心像素
p
p
p
的邻域。
I
(
∗
)
I(*)
I
(
∗
)
表示像素点
∗
*
∗
处的灰度值,⊗为比特位的逐位连接运算。
ξ
(
)
ξ()
ξ
(
)
运算则由下面公式定义:
ξ
(
I
(
p
)
,
I
(
q
)
)
=
{
0
I
(
q
)
≤
I
(
p
)
1
I
(
q
)
≥
I
(
p
)
ξ(I(p), I(q)) = \left\{ \begin{matrix} 0 & I(q) ≤ I(p) \\ 1 & I(q) ≥ I(p) \end{matrix} \right.
ξ
(
I
(
p
)
,
I
(
q
))
=
{
0
1
I
(
q
)
≤
I
(
p
)
I
(
q
)
≥
I
(
p
)
通过上文的公式可以得到了Cencus变换的一串二进制,基于Census变换的匹配代价计算方法是计算左右影像对应的两个像素的Census变换值的汉明(Hamming)距离,即匹配代价为:
C
C
e
n
c
u
s
=
H
a
m
m
i
n
g
(
T
(
p
)
,
T
(
q
)
)
C_{Cencus} = Hamming(T(p),T(q))
C
C
e
n
c
u
s
=
H
ammin
g
(
T
(
p
)
,
T
(
q
))
其中,
T
(
p
)
T( p)
T
(
p
)
为左图产生的二进制串,
T
(
q
)
T(q)
T
(
q
)
为右图产生的二进制串。Hamming距离即两个比特串的对应位不相同的数量,计算方法为将两个比特串进行亦或运算,再统计异或运算结果中的比特位中为1的个数。
我们可以通过下图辅助理解Cencus匹配代价的计算方法,先分别计算出左图和右图中一定范围的Cencus变换的二进制串结果(上文已经介绍),然后对得到的两串二进制进行异或操作,得到结果中1的个数即为所求匹配代价(下图结果为2)。
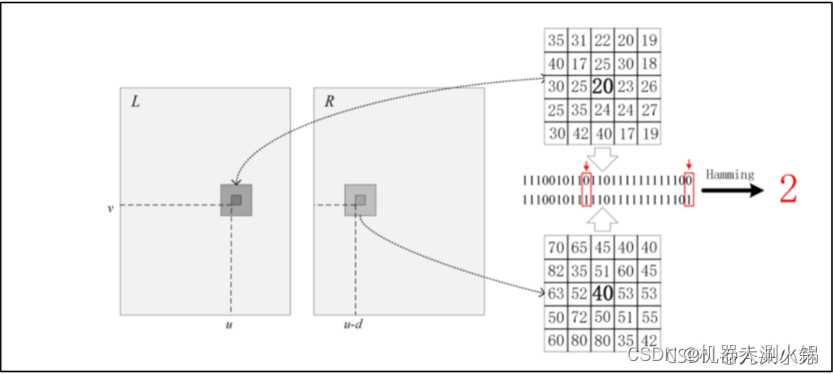
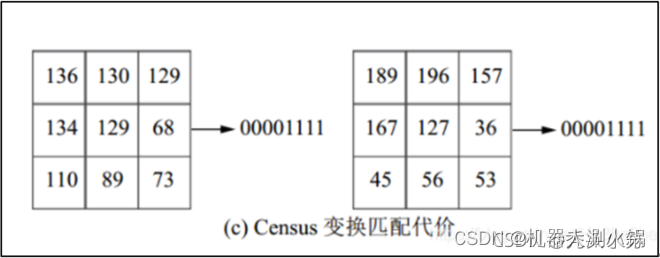
我们前面说到,AD和SAD算法都对光照较为敏感,这里的Cencus变换则对图片的明暗变化并不敏感,因为Cencus算法是比较的相对灰度关系,所以即使左右影像亮度不一致,也能得到较好的匹配效果。但是Cencus变换对重复区域的匹配效果不好,例如下图的两个领域窗口中灰度完全不同,但Cencus变换得到的代价完全相同。
3、代价聚合
代价聚合的根本目的是让代价值能够准确的反映像素之间的相关性。匹配代价计算后,可以得到一个代价矩阵C(DSI),矩阵C中存储了每个像素在视差范围内各个视差下的匹配代价值。此时的代价矩阵C的效果还比较差,因为代价计算只考虑了局部的相关性,通过两个像素邻域内一定大小的窗口内的像素信息来计算代价值,这很容易受到影像噪声的影响,而且当影像处于弱纹理或重复纹理区域,这个代价值极有可能无法准确的反映像素之间的相关性,直接表现就是真实同名点的代价值非最小。
而代价聚合则是建立邻接像素之间的联系,以一定的准则,如相邻像素应该具有连续的视差值,来对代价矩阵进行优化,这种优化往往是全局的,每个像素在某个视差下的新代价值都会根据其相邻像素在同一视差值或者附近视差值下的代价值来重新计算,得到新的DSI,用矩阵S来表示。
实际上代价聚合类似于一种视差传播步骤,信噪比高的区域匹配效果好,初始代价能够很好的反映相关性,可以更准确的得到最优视差值,通过代价聚合传播至信噪比低、匹配效果不好的区域,最终使所有影像的代价值都能够准确反映真实相关性。常用的代价聚合方法有扫描线法、动态规划法、SGM算法中的路径聚合法等。
4、视差计算
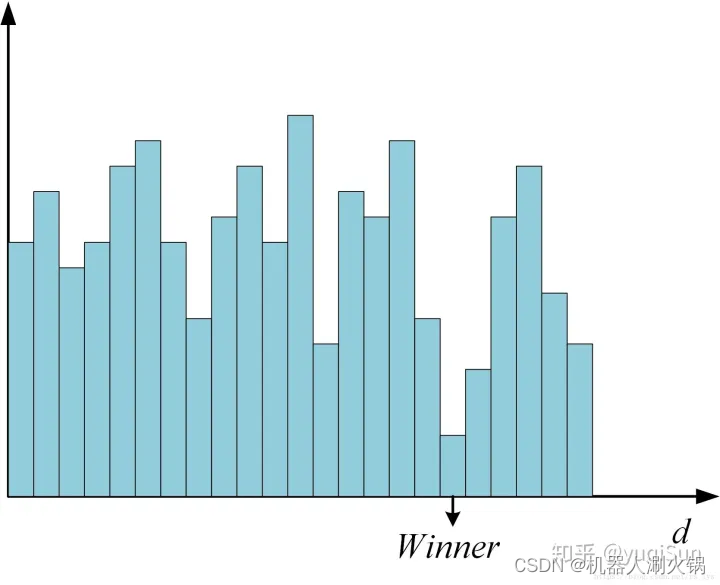
视差计算即通过代价聚合之后的代价矩阵S来确定每个像素的最优视差值,通常使用赢家通吃算法(WTA,Winner-Takes-All)来计算,如图2所示,即某个像素的所有视差下的代价值中,选择最小代价值所对应的视差作为最优视差。这一步非常简单,这意味着聚合代价矩阵S的值必须能够准确的反映像素之间的相关性,也表明上一步代价聚合步骤是立体匹配中极为关键的步骤,直接决定了算法的准确性。
5、视差优化
视差优化的目的是对上一步得到的视差图进行进一步优化,改善视差图的质量。主要有以下步骤:
- 左右一致性检测:剔除因为遮挡和噪声而导致的错误视差
- 错误像素分类 :
- 区域投票 : 剔除孤立异常点
- 正确插值 :
- 边缘修正 :
- 亚像素增强 :子像素精度优化
-
中值滤波 :对视差图进行平滑
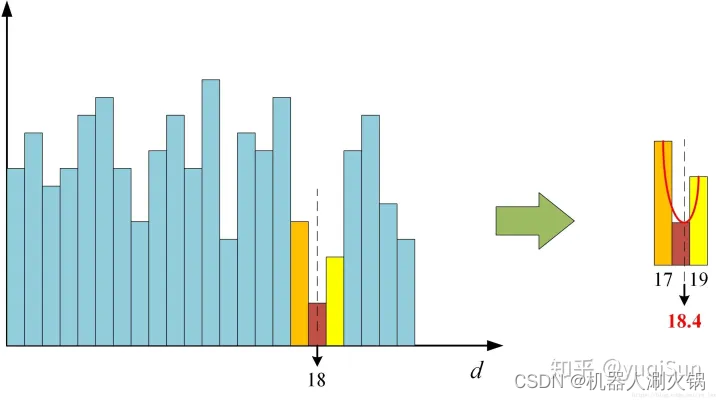
由于WTA算法所得到的视差值是整像素精度,为了获得更高的子像素精度,需要对视差值进行进一步的子像素细化,常用的子像素细化方法是一元二次曲线拟合法,通过最优视差下的代价值以及左右两个视差下的代价值拟合一条一元二次曲线,取二次曲线的极小值点所代表的视差值为子像素视差值。如图所示。