左式堆是堆的一种,但是左式堆是建立在一个具有堆序性的二叉树上而不是二叉堆
左式堆和二叉堆的共同点:
- 左式堆具有和二叉堆一样的堆序性
- 左式堆具有和二叉堆一样的结构性
左式堆和二叉堆的不同点:
- 左式堆虽然和二叉堆都是二叉树,但是左式堆和二叉堆不同的是,二叉堆接近完全完全二叉树,左式堆是不理想平衡的,更加直接的说,左式堆是趋向于非常不平衡的。
左式堆的一些概念
-
零路经长(NPL)
- 左式堆的零路经长是定义为从节点X开始到一个不具有两个儿子的节点的最短路径的长,具有两个儿子的节点NPL = 1,具有一个或者没有儿子的节点的NPL = 0,NPL(null)= -1;
- 左式堆的任意节点的左孩子的NPL要大于或等于右孩子
- 任一节点的NPL比他各个儿子的NPL的最小值大1
-
定理
-
在右路径上有R个节点的左子树必然具有的节点数为
2R
−
1
2^R-1
2
R
−
1
-
在右路径上有R个节点的左子树必然具有的节点数为
左式堆的合并
对左式堆的基本操作就是合并,这也是左式堆中比较重要的操作,左式堆合并是很多其他操作的基础,比如向左式堆中插入元素和删除左式堆根节点等操作都基于合并来进行

先比较根值,h1是较小根植堆,h2是较大根值堆,应该递归的将较大根值的堆与较小根值堆的右子堆合并

又可以看成是两个堆的合并

8<6 .所以h1的【较大根值】右子堆(h1R)和【较小根植】h2的右子堆合并

以此递归执行,最后合并结果

/**
* 合并堆(递归实现)
* @param h1
* @param h2
* @return
*/
private Node<AnyType> merge(Node<AnyType> h1,Node<AnyType> h2){
//如果合并的两堆中,有一个是空堆,则不需要合并,直接返回非空堆
if(h1 == null) {
return h2;
}
if (h2 == null) {
return h1;
}
//将具有较大根值的堆和较小根值的堆的右子堆合并
if(h1.element.compareTo(h2.element)<0) {
return merge1(h1, h2);
}else {
return merge1(h2, h1);
}
}
/**
* 合并堆 (递归实现)---O(logN)(真正实现堆的合并操作)
* @param h1
* @param h2
* @return
*/
private Node<AnyType> merge1(Node<AnyType> h1,Node<AnyType> h2){
//h1是较小根值的堆,h2是较大根植的堆长
//如果h1的左子堆是空堆,则左子堆的零路径长<右子堆,不满足左子堆零路径>右子堆,所以,直接将h2合并到h1左子堆
if(h1.left == null) {
h1.left = h2;
}else {
//否则,则将较大根值得堆合并到较小根值的堆的右子堆
h1.right = merge(h1.right, h2);
//比较合并后的左右子堆的零路经长是否满足左子堆零路径>右子堆
//不满足则交互左右堆
if(h1.left.npl < h1.right.npl) {
swapChild(h1);
}
h1.npl = h1.right.npl+1;
}
return h1;
}
斜堆
斜堆是左式堆的自调节形式,斜堆和左式堆的关系类似于伸展树和平衡树,斜堆是具有堆序的二叉树,但是不对树有结构限制,不同于做左式堆,斜堆没有NPL的概念,斜堆的右路径在任何时刻都是可以任意长的
斜堆的合并
斜堆的合并操作和左式堆的相似,但是左式堆在NPL上有要求,斜堆是没有要求的,因此斜堆的交换是无条件的,除了那些右路径上的所有节点的最大者不交换他的左右儿子的例外外,我们都要进行这种交换
假设我们要合并与上边一样的h1和h2,跟左式堆合并一样,先比较要合并两堆的根节点,将较大根节点和较小根节点的右子节点进行合并

开始跟左式堆的合并一样

合并完成,因为我们之前的合并都是沿着右路径进行的,所以合并后,右路径长度必然会增加,这会影响下一次合并的效率,所以合并后,我们需要通过交换左右子树,降低右路径长度,因为斜堆是不记录节点的距离,所以沿着合并的路径,在每个节点交换左右子树
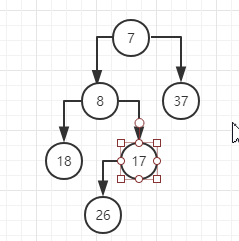
通过递归完整合并过程
