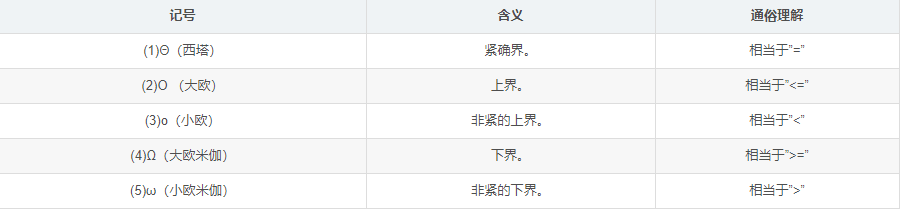
在算法分析中,经常会遇到以下几种渐进符号
-
渐近精确界记号:
Θ
Θ(big-theta)
-
渐近上界记号 :
O
O(big-oh)
-
渐近下界记号 :
Ω
Ω(big-omege)
- 非渐近紧确上界:o(小-oh)
- 非渐近紧确下界:ω(小-omege)
下面对渐进符号进行详解:
大写O符号
f(n)=O(g(n)),这里f(n)是分析出来算法的执行次数的函数,
O的定义:
当且仅当存在正的常数c和n0,使得对于所有的n>=n0,有f(n)<=cg(n)。
这里cg(n)就是函数f(n)的上限。讲到这是不是很迷糊,我刚开始也这样,不着急,看下面例子,你就会恍然大悟啦。
几种函数的例子:
1.线性函数
f(n)=3n+2,当n>=2时,3n+2<=3n+n=4n。
所以f(n)=O(n),这里c = 4,n0 = 2,g(n) = n, 那么cg(n) 也就是4n 就是f(n) 的上界
2.平方函数
f(n)=2n^2+3n+3,当n>=3时,3n+3<=4n,当n>=4时,4n<n^2,f(n)=2n^2+n^2=3n^2。
f(n)=O(n^2),这里c = 3,n0 = 4, g(n) = n^2 ,那么cg(n) 也就是3n^2 就是f(n) 的上界
3.指数函数
f(n)=6*2^n+n^2,当n>=4时,n^2<=2^n,所以当n>=4,有f(n)<=6*2^n+2^n=7*2^n。
这里c是7,n0=4,f(n)=O(2^n)。
4.常数阶
f(n)=9,这里就直接记为O(1),c为9,n0为0就可以了,f(n)=9<=9*1。
Ω符号
定义:
f(n)=Ω(g(n)),当且仅当存在正的常数c和n0,使得对于所有n>=n0,有f(n)>=cg(n)。
Ω符号是给函数的下限。
例子:
对于所有的n,有f(n)=3n+2>3n,所以f(n)=Ω(n),这里c=3,n0=0。这里也可以这样f(n)=Ω(1),
Θ符号
定义:
对于存在大于0的常数c1、c2和非负的整数n0,以及足够大的n,对于所有的n≥n0来说,有c1g(n)<=f
(n)<=c2g(n)。
例子:
3n+2=Θ(n),当c1=3,c2=4,n>=n0=2时,3n<=3n+2<=4n。
小写o符号
定义:
f(n)=o(g(n)),当且仅当f(n)=O(g(n)) 且f(n)!=Ω(g(n))。
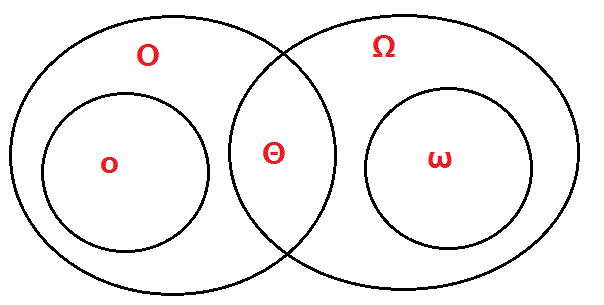
渐近记号Θ、Ο、o、Ω、ω关系