什么是汉明码
汉明码是一种线性分组码。线性分组码是指将信息码序列划分为长度为k的序列段,在每一段后面附加r位的监督码,且监督码和信息码之间构成线性关系,即它们之间可由线性方程组来联系。这样构成的抗干扰码称为线性分组码。其中监督码和信息码之间的关系计算结果称为校正子(英文Syndrome)。
汉明码被常用在通讯领域的编码和纠错,也用于内存ECC纠错。
汉明码长度
设码长为n,信息码序列长度为k,监督码长度为r= n – k。
如果需要纠正一位出错,因为长度为n的序列上每一位都可能出错,一共有n种情况,另外还有不出错的情况,所以我们必须用长度为r的监督码表示出n+1种情况。
而长度为r的监督码一共可以表示2
^
r种情况。
因此必须满足:
2
^
r >= n + 1,即r>= log(n+1)。
举例:
1) 假如中k = 8, r = 4。显然,2的4次方等于16,大于8+4+1=13。
2) 如果要校验纠正的数据长度为64位,先将64以2为底求对数,结果为6;再计算64+6+1=71,那么显然汉明码也得用7位(2的7次方为128,大于64+7+1=72)。
汉明码校验关系公式
我们以一个例子来说明。假设k=4,需要纠正一位错误,则:
2^r >= n + 1 = k + r + 1 = 4 + r + 1
解得r >= 3。我们取r=3,则码长为3+4=7。用b1,b2, b3…b7位置表示这7个码元。用S1,S2, S3表示三个监督关系式中的校正子。我们作如下规定(这个规定是任意的):
|
S3 |
S2 |
S1 |
线性码各bit位置 |
|
0 |
0 |
0 |
无错 |
|
0 |
0 |
1 |
b1 |
|
0 |
1 |
0 |
b2 |
|
0 |
1 |
1 |
b3 |
|
1 |
0 |
0 |
b4 |
|
1 |
0 |
1 |
b5 |
|
1 |
1 |
0 |
b6 |
|
1 |
1 |
1 |
b7 |
那么
按
照表中的规定可知,我们比较容易得出,仅当一个错码位置在b1,b3, b5或b7时,校正子S1为1,否则S1为0,即:
S1 = XOR(b1, b3, b5, b7) (公式1)
备注:上述公式可能被写做
S1 = b1⊕b3⊕b5⊕b7
同理,可以得到:
S2 = XOR(b2, b3, b6, b7) (公式2)
S3 = XOR(b4, b5, b6, b7) (公式3)
汉明码监督码位置以及计算公式
继续以上面的S1,S2,S3作为例子,下面我们推算监督码计算公式,我们以P1,P2,P3来表示监督码,以D1,D2, D3, D4来表示信息码:
方案一:
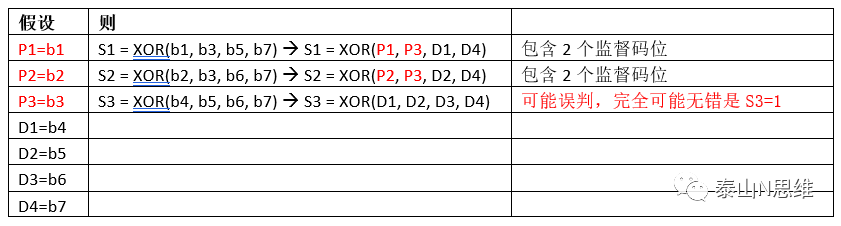
结论:该方案不可行!
由此可见,监督码并不是可以放在任意位置。
方案二:
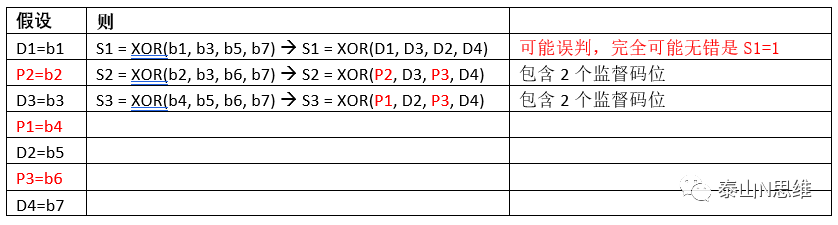
结论:该方案不可行!
似乎监督码的位置需要符合一定的条件?我们继续尝试。
方案三:
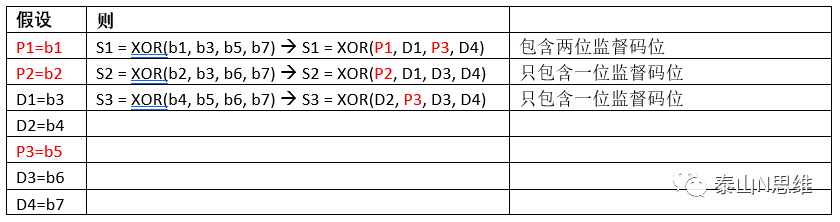
如果无错, 则S1 = 0,根据S1的计算公式可得:
S1 = XOR(P1,D1,P3,D4) = 0
算是中包含P1和P3两个未知变量,无法进一步计算。那我们先计算P2和P3。
无错条件下,S2= 0,根据S2的计算公式可得:
S2 = XOR(P2, D1, D3, D4) = 0 —>
P2 = XOR(D1, D3, D4)。
同理,无错条件下,S3= 0,根据S3的计算公式可得:
S3= XOR(D2, P3, D3, D4) = 0 —>
P3 = XOR(D2, D3,D4)。
再回头计算S1:
S1 = XOR(P1,D1,P3,D4) = 0 —>
P1 = XOR(D1, P3,D4) —>
P1 = XOR(D1, D2, D3, D4, D4) = XOR(D1, D2, D3)
结论:该方案可得出有效的监督码计算公式,但是计算步骤略显复杂。我们继续尝试其他方案。
方案四:
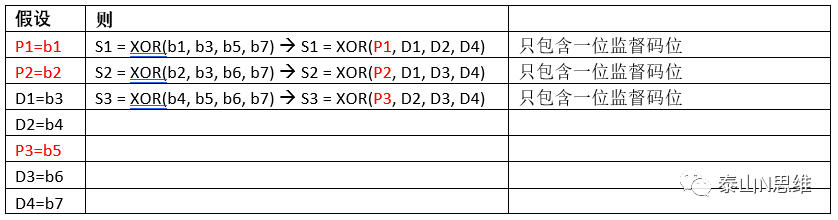
根据无错条件下,S1 = 0,S2 = 0,S3 = 0,我们同样可以简单推导出P1,P2和P3的公式:
S1 = XOR(P1, D1, D2, D4) = 0 —> P1 = XOR(D1, D2, D4)
S2= XOR(P2, D1, D3, D4) = 0 —> P2 = XOR(D1, D3, D4)
S3= XOR(P3, D2, D3, D4) = 0 —> P3 = XOR(D2, D3, D4)
结论:该方案可以得出有效监督码计算公式,并且计算简单快速。
比较各个方案,我们可以发现,监督码的位置有如下规律:
1. 使得任一校验子计算公式里面包含至少一个监督码位;
2. 任一信息码位至少要被包含在一个校验子计算公式中,才能保证该信息码位被监督;
3. 每个校验子计算公式仅包含一个监督码位,能让监督码和校验子计算更简单和快速。
根据上述规律总结,其实我们很容易从最开始的S1,S2,S3计算公式(1)(2)(3)得出方案四位一较佳方案。这也是汉明码标准将监督码位放在1,2,4,8等2的指数位的原因,该方案满足上述规律3。
汉明码纠错举例
下面,我们分别用方案三和方案四来进行校验举例。
先用方案三举例,假设传输信息码1011b:

假设P3出错反转 纠错结果[S3:S1]=101b=5

纠错结果正确!方案三中,P3在b5位置!
假设D2出错反转 纠错结果[S3:S1]=100b=4

纠错结果正确!方案三中,D2在b4位置!
再用方案四来举例,仍然假设传输信息码1011b:

假设D2出错反转 纠错结果[S3:S1]=101b=5
 纠错结果正确!方案四中,D2在b5位置!
纠错结果正确!方案四中,D2在b5位置!
延伸阅读
汉明码不仅仅能发现并纠正一位错误,可以通过增加最小汉明距,增加监督码位(有时也称为冗余位),实现更多位的错误发现和纠正。并且,监督码位跟检错和纠错的能力还具有一定的关系。在阐述这个关系之前,先需要解释汉明距。
定义1:
在一个码组集合中,任意两个码字(包含信息码和监督码的一个完整码位的组合)之间对应位上码位取值不同的位的数目定义为这两个码字之间的汉明距离。
例如:(00)与(01)的距离是1(只有1位不同),(110)和(101)的距离是2(有2位不同)。
定义2:
在一个码组集合中,任意两个编码之间汉明距离的最小值称为这个码组的最小汉明距离。
下面我们用d表示码组的最小汉明距离。最小码距跟纠错能力有如下关系:
1.当码组用于检测错误时,设可检测e个位的错误,则 d >= e + 1
2.若码组用于纠错,设可纠错t个位的错误,则
d >= 2t+1
3.如果码组用于纠正t个错,检测e个错,则
d >= e+t+1
, 这里e>t
现在举个例子来说明这个问题:
假如我们现在要对A,B两个字母进行编码。我们可以选用不同长度的编码,以产生不同码距的编码,分析它们的检错纠错能力。若用1位长度的二进制编码。若A=1,B=0。这样A,B之间的最小码距为1。
合法码:{0,1};
非法码:{0,1};
根据上面的规则可知此编码的检错纠错能力均为0,即无检错纠错能力。其实道理很简单,这种编码无论由1错为0,或由0错为1,接收端都无法判断是否有错,因为1,0都是合法的编码。
若用2位长度的二进制编码,可选用11,00作为合法编码,也可以选用01,10作为合法编码。若以A=11,B=00为例,A、B之间的最小码距为2。
合法码:{11,00};
非法码:{01,10};
根据上面的规则可知此编码的检错位数为1位,无法纠错。因为无论A(11)或B(00),如果发生一位错码,必将变成01或10,这都禁用码组(非法码),故接收端可以判断为误码,却不能纠正其错误。因为无法判断误码(01或10)是A(00)错误还是B(11)错误造成,即无法判断原信息是A或B,或说A与B形成误码(01或10)的可能性(概率)是相同的。如果产生二位错码,即00错为11,或11错为00,结果将从一个合法编变成另一个合法编码,接收端就无法判断其是否有错。所以此种编码的检错能力为1位,纠错能力为0位。
若用3位长度的二进制编码,可选用111,000作为合法编码。A,B之间的最小码距为3。
合法码:{111,000};
非法码:{001,010,011,100,101,110};
根据上面的规则可知此编码的检错位数为2位,纠错位数为1位。例如:当信息A(000)产生1位错误时,将有3种误码形式,即001或010或100,这些都是禁用码组,可确定是误码。而有这3个误码与合法编码000的距离最近,与合编码111的距离较远,根据误码少的概率大于误码多的概率的规律,可以判定原来的正确码组为000,只要把误码中的1改为0即可得到纠正。同理,如果信息B(111)产生1位错误时,则有另三种误码可能产生,即110,101,011,根据同样道理可以判定原来的正确码组是111,并能纠正错误。
但是,如果信息A(000)或信息B(111)产生两位错误时,虽然能根据禁用码组识别其错误,但纠错时去会做出错误的纠正而造成“误纠错”。
如果信息A(000)或信息B(111)产生三位错误时,将从一个合法编码A(或B)变成了另一个合法编码B(或A),这时既检不出错,更不会纠错了,因为误码已成为合法编码,译码后必然产生错误。所以检错位数为2位,纠错位数为1位。