无人驾驶算法——使用Stanley method实现无人车轨迹追踪
文章已搬至
知乎
,如果对你有所帮助和启发,欢迎关注,点赞,评论交流,感谢
Date: 2019/08/03
Editor:萧潇子(Jesse)
Contact: 1223167600@qq.com
基于几何追踪的方法
关于无人车追踪轨迹,目前的主流方法分为两类:基于几何追踪的方法和基于模型预测的方法,其中几何追踪方法主要包含纯跟踪和Stanley两种方法,纯跟踪方法已经广泛应用于移动机器人的路径跟踪中,网上也有很多详细的介绍,本文主要介绍斯坦福大学无人车使用的Stanley方法。
Stanley method
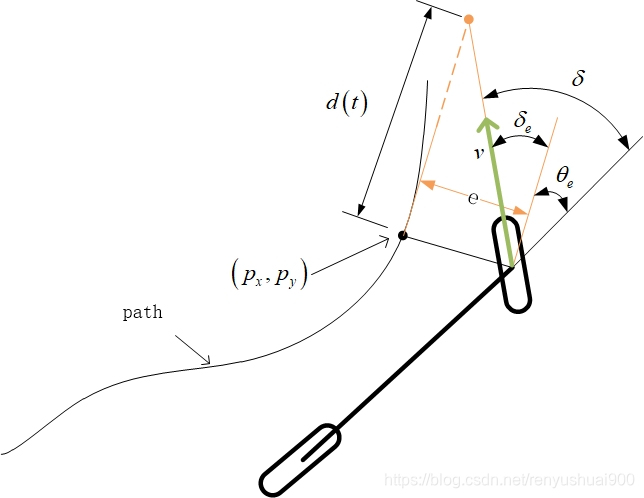
Stanley方法是一种基于横向跟踪误差(cross-track error :
e
e
e
为前轴中心到最近路径点
(
p
x
,
p
y
)
(p_x, p_y)
(
p
x
,
p
y
)
的距离)的非线性反馈函数,并且能实现横向跟踪误差指数收敛于0。根据车辆位姿与给定路径的相对几何关系可以直观的获得控制车辆方向盘转角的控制变量,其中包含横向偏差
e
e
e
和航向偏差
θ
e
\theta_e
θ
e
。
δ
(
t
)
=
δ
e
(
t
)
+
δ
θ
e
(
t
)
\delta(t) = \delta_{e}(t) + \delta_{\theta_{e}}(t)
δ
(
t
)
=
δ
e
(
t
)
+
δ
θ
e
(
t
)
-
在不考虑横向跟踪误差的情况下,前轮偏角和给定路径切线方向一致,如图所示。其中
θe
\theta_e
θ
e
表示车辆航向与最近路径点切线方向之间的夹角,在没有任何横向误差的情况下,前轮方向与所在路径点的方向相同:
δθ
e
(
t
)
=
θ
e
(
t
)
\delta_{\theta_{e}}(t) = \theta_e(t)
δ
θ
e
(
t
)
=
θ
e
(
t
)
-
在不考虑航向跟踪偏差的情况下,横向跟踪误差越大,前轮转向角越大,假设车辆预期轨迹在距离前轮
d(
t
)
d(t)
d
(
t
)
处与给定路径上最近点切线相交,根据几何关系得出如下非线性比例函数:
δe
(
t
)
=
arctan
e
(
t
)
d
(
t
)
=
arctan
k
e
(
t
)
v
(
t
)
\delta_{e}(t) = \arctan\frac{e(t)}{d(t)} = \arctan\frac{ke(t)}{v(t)}
δ
e
(
t
)
=
arctan
d
(
t
)
e
(
t
)
=
arctan
v
(
t
)
k
e
(
t
)
其中
d(
t
)
d(t)
d
(
t
)
与车速相关,最后用车速
v(
t
)
v(t)
v
(
t
)
,增益参数
kk
k
表示。随着横向误差的增加,
ar
c
t
a
n
arctan
a
r
c
t
a
n
函数产生一个直接指向期望路径的前轮偏角,并且收敛受车速
v(
t
)
v(t)
v
(
t
)
限制。
综合两方面控制因素,基本转向角控制率如下:
δ(
t
)
=
θ
e
(
t
)
+
arctan
k
e
(
t
)
v
(
t
)
\delta(t) = \theta_e(t) + \arctan\frac{ke(t)}{v(t)}
δ
(
t
)
=
θ
e
(
t
)
+
arctan
v
(
t
)
k
e
(
t
)
使用线性自行车运动模型,可以得到横向误差的变化率:
e˙
(
t
)
=
−
v
(
t
)
sin
δ
e
(
t
)
\dot{e}(t) = -v(t)\sin\delta_{e}(t)
e
˙
(
t
)
=
−
v
(
t
)
sin
δ
e
(
t
)
其中
sin
δ
e
(
t
)
\sin\delta_{e}(t)
sin
δ
e
(
t
)
根据几何关系可知:
sin
δ
e
(
t
)
=
e
(
t
)
d
(
t
)
2
+
(
e
(
t
)
)
2
=
k
e
(
t
)
v
(
t
)
2
+
(
k
e
(
t
)
)
2
\sin\delta_{e}(t) = \frac{e(t)}{\sqrt{d(t)^{2}+(e(t))^{2}}} = \frac{ke(t)}{\sqrt{v(t)^{2}+(ke(t))^{2}}}
sin
δ
e
(
t
)
=
d
(
t
)
2
+
(
e
(
t
)
)
2
e
(
t
)
=
v
(
t
)
2
+
(
k
e
(
t
)
)
2
k
e
(
t
)
so:
e˙
(
t
)
=
−
v
(
t
)
k
e
(
t
)
v
(
t
)
2
+
(
k
e
(
t
)
)
2
=
−
k
e
(
t
)
1
+
(
k
e
(
t
)
v
(
t
)
)
2
\dot{e}(t) = \frac{-v(t)ke(t)}{\sqrt{v(t)^{2}+(ke(t))^{2}}} = \frac{-ke(t)}{\sqrt{1+\Bigg(\frac{ke(t)}{v(t)}\Bigg)^{2}}}
e
˙
(
t
)
=
v
(
t
)
2
+
(
k
e
(
t
)
)
2
−
v
(
t
)
k
e
(
t
)
=
1
+
(
v
(
t
)
k
e
(
t
)
)
2
−
k
e
(
t
)
当横向跟踪误差
e
(
t
)
e(t)
e
(
t
)
很小时,
(
k
e
(
t
)
/
v
(
t
)
)
2
→
0
(ke(t)/v(t))^{2}\to0
(
k
e
(
t
)
/
v
(
t
)
)
2
→
0
:
e
˙
(
t
)
≈
−
k
e
(
t
)
\dot{e}(t) \approx -ke(t)
e
˙
(
t
)
≈
−
k
e
(
t
)
通过积分上式:
e
(
t
)
=
e
(
0
)
×
exp
−
k
t
e(t) = e(0)\times\exp^{-kt}
e
(
t
)
=
e
(
0
)
×
exp
−
k
t
因此横向误差指数收敛于
e
(
t
)
=
0
e(t) = 0
e
(
t
)
=
0
,参数
k
k
k
决定了收敛速度。对于任意横向误差,微分方程都单调的收敛到0。
基于Python的Stanley算法跟踪直线仿真
Stanley控制转向角度,使用一个简单的P控制器控制速度,首先我们定义参数数值如下:
import numpy as np
import math
import matplotlib.pyplot as plt
k = 0.5 # 增益参数
Kp = 1.0 # 速度P控制器系数
dt = 0.1 # 时间间隔,单位:s
L = 3.0 # 车辆轴距,单位:m
这里将增益参数
k
k
k
设置为0.3,速度P控制器的比例系数Kp设置为1.0,时间间隔为0.1 秒,车的轴距我们定为3.0米。
定义车辆状态类,在简单的自行车模型中,我们只考虑车辆的当前位置
(
x
,
y
)
(x,y)
(
x
,
y
)
,车辆的偏航角度
y
a
w
yaw
y
a
w
以及车辆的速度
v
v
v
,为了仿真模拟,我们定义车辆的状态更新函数来模拟真实车辆的状态更新:
class VehicleState:
def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0):
self.x = x
self.y = y
self.yaw = yaw
self.v = v
def update(state, a, delta):
state.x = state.x + state.v * math.cos(state.yaw) * dt
state.y = state.y + state.v * math.sin(state.yaw) * dt
state.yaw = state.yaw + state.v / L * math.tan(delta) * dt
state.v = state.v + a * dt
return state
仿真中,纵向控制使用一个简单的P控制器,横向控制(即转角控制)使用Stanley控制器,并且限制车轮转角范围[-30, 30],这两个控制器定义如下:
def PControl(target, current):
a = Kp * (target - current)
return a
def stanley_control(state, cx, cy, ch, pind):
ind = calc_target_index(state, cx, cy)
if pind >= ind:
ind = pind
if ind < len(cx):
tx = cx[ind]
ty = cy[ind]
th = ch[ind]
else:
tx = cx[-1]
ty = cy[-1]
th = ch[-1]
ind = len(cx) - 1
# 计算横向误差
if ((state.x - tx) * th - (state.y - ty)) > 0:
error = abs(math.sqrt((state.x - tx) ** 2 + (state.y - ty) ** 2))
else:
error = -abs(math.sqrt((state.x - tx) ** 2 + (state.y - ty) ** 2))
delta = ch[ind] - state.yaw + math.atan2(k * error, state.v)
# 限制车轮转角 [-30, 30]
if delta > np.pi / 6.0:
delta = np.pi / 6.0
elif delta < - np.pi / 6.0:
delta = - np.pi / 6.0
return delta, ind
定义函数用于搜索最临近的路点:
def calc_target_index(state, cx, cy):
# 搜索最临近的路点
dx = [state.x - icx for icx in cx]
dy = [state.y - icy for icy in cy]
d = [abs(math.sqrt(idx ** 2 + idy ** 2)) for (idx, idy) in zip(dx, dy)]
ind = d.index(min(d))
return ind
主函数:
def main():
# 设置目标路点
cx = np.arange(0, 50, 1)
cy = [0 * ix for ix in cx]
ch = [0 * ix for ix in cx]
target_speed = 5.0 / 3.6 # [m/s]
T = 200.0 # 最大模拟时间
# 设置车辆的初始状态
state = VehicleState(x=-0.0, y=-3.0, yaw=-0.0, v=0.0)
lastIndex = len(cx) - 1
time = 0.0
x = [state.x]
y = [state.y]
yaw = [state.yaw]
v = [state.v]
t = [0.0]
target_ind = calc_target_index(state, cx, cy)
while T >= time and lastIndex > target_ind:
ai = PControl(target_speed, state.v)
di, target_ind = stanley_control(state, cx, cy, ch, target_ind)
state = update(state, ai, di)
time = time + dt
x.append(state.x)
y.append(state.y)
yaw.append(state.yaw)
v.append(state.v)
t.append(time)
plt.cla()
plt.plot(cx, cy, ".r", label="course")
plt.plot(x, y, "-b", label="trajectory")
plt.plot(cx[target_ind], cy[target_ind], "go", label="target")
plt.axis("equal")
plt.grid(True)
plt.title("Speed[km/h]:" + str(state.v * 3.6)[:4])
plt.pause(0.001)
if __name__ == '__main__':
main()
仿真结果:
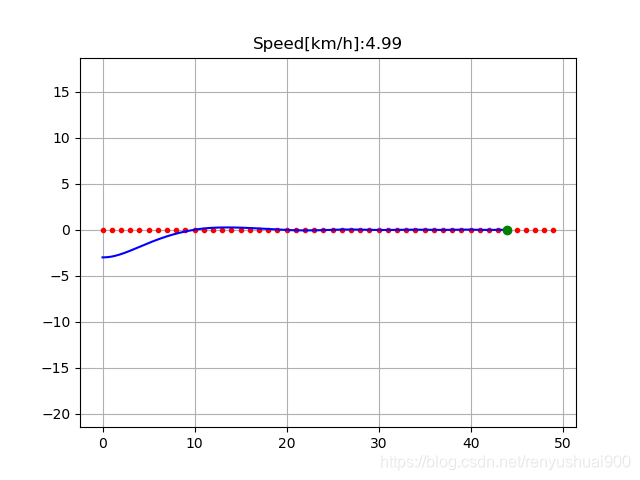
通过仿真结果图,我们看到红点表示实现规划好的直线路径,蓝线则表示我们的车辆实际运行的轨迹,绿点表示距离当前位置最近路径点,在这段代码中,我们设置了增益参数
k
k
k
为0.3,通过进一步去改变
k
k
k
的大小对比结果,可以减小
k
k
k
值得到更平滑的跟踪轨迹,但是更加平滑的结果会引起某些急剧的转角处会存在转向不足的情况。
参考
- Automatic Steering Methods for Autonomous Automobile Path Tracking
- Stanley_ The robot that won the DARPA grand challenge
- 无人驾驶汽车系统入门(十八)——使用pure pursuit实现无人车轨迹追踪(https://blog.csdn.net/adamshan/article/details/80555174)