在常见的边缘检测算子或轮廓检测相关算法中都有非极大值抑制这一步,然而对与非极大值抑制在这些边缘检测算子中应用,在理解可能有点似懂非懂。本文将介绍Canny算法中的非极大值抑制,Canny算子中的非极大值抑制是指沿着梯度方向上进行非极大值的抑制。
首先,我们来看看Canny算子中非极大值抑制的一段代码(可以略过):
/*
fucntion: non-maximum suppression
input:
pMag: pointer to Magnitude,
pGradX: gradient of x-direction
pGradY: gradient of y-direction
sz: size of pMag (width = size.cx, height = size.cy)
output:
pNSRst: result of non-maximum suppression
*/
void NonMaxSuppress(int*pMag,int* pGradX,int*pGradY,SIZE sz,LPBYTE pNSRst)
{
LONG x,y;
int nPos;
// the component of the gradient
int gx,gy;
// the temp varialbe
int g1,g2,g3,g4;
double weight;
double dTemp,dTemp1,dTemp2;
//设置图像边缘为不可能的分界点
for(x=0;x<sz.cx;x++)
{
pNSRst[x] = 0;
pNSRst[(sz.cy-1)*sz.cx+x] = 0;
}
for(y=0;y<sz.cy;y++)
{
pNSRst[y*sz.cx] = 0;
pNSRst[y*sz.cx + sz.cx-1] = 0;
}
for (y=1;y<sz.cy-1;y++)
{
for (x=1;x<sz.cx-1;x++)
{
nPos=y*sz.cx+x;
// if pMag[nPos]==0, then nPos is not the edge point
if (pMag[nPos]==0)
{
pNSRst[nPos]=0;
}
else
{
// the gradient of current point
dTemp=pMag[nPos];
// x,y 方向导数
gx=pGradX[nPos];
gy=pGradY[nPos];
//如果方向导数y分量比x分量大,说明导数方向趋向于y分量
if (abs(gy)>abs(gx))
{
// calculate the factor of interplation
weight=fabs(gx)/fabs(gy);
g2 = pMag[nPos-sz.cx]; // 上一行
g4 = pMag[nPos+sz.cx]; // 下一行
//如果x,y两个方向导数的符号相同
//C 为当前像素,与g1-g4 的位置关系为:
//g1 g2
// C
// g4 g3
if(gx*gy>0)
{
g1 = pMag[nPos-sz.cx-1];
g3 = pMag[nPos+sz.cx+1];
}
//如果x,y两个方向的方向导数方向相反
//C是当前像素,与g1-g4的关系为:
// g2 g1
// C
// g3 g4
else
{
g1 = pMag[nPos-sz.cx+1];
g3 = pMag[nPos+sz.cx-1];
}
}
else
{
//插值比例
weight = fabs(gy)/fabs(gx);
g2 = pMag[nPos+1]; //后一列
g4 = pMag[nPos-1]; // 前一列
//如果x,y两个方向的方向导数符号相同
//当前像素C与 g1-g4的关系为
// g3
// g4 C g2
// g1
if(gx * gy > 0)
{
g1 = pMag[nPos+sz.cx+1];
g3 = pMag[nPos-sz.cx-1];
}
//如果x,y两个方向导数的方向相反
// C与g1-g4的关系为
// g1
// g2 C g4
// g3
else
{
g1 = pMag[nPos-sz.cx+1];
g3 = pMag[nPos+sz.cx-1];
}
}
dTemp1 = weight*g1 + (1-weight)*g2;
dTemp2 = weight*g3 + (1-weight)*g4;
//当前像素的梯度是局部的最大值
//该点可能是边界点
if(dTemp>=dTemp1 && dTemp>=dTemp2)
{
pNSRst[nPos] = 128;
}
else
{
//不可能是边界点
pNSRst[nPos] = 0;
}
}
}
}
}
在上面代码中,有几个IF-ELSE需要注意。在John Canny提出的Canny算子的论文中,非最大值抑制就只是在0、90、45、135四个梯度方向上进行的,每个像素点梯度方向按照相近程度用这四个方向来代替。这种情况下,非最大值抑制所比较的相邻两个像素就是:
1) 0:左边 和 右边
2)45:右上 和 左下
3)90: 上边 和 下边
4)135: 左上 和 右下
这样做的好处是简单, 但是这种简化的方法无法达到最好的效果, 因为,自然图像中的边缘梯度方向不一定是沿着这四个方向的。因此,就有很大的必要进行插值,找出在一个像素点上最能吻合其所在梯度方向的两侧的像素值。
然而,实际数字图像中的像素点是离散的二维矩阵,所以处在真正中心位置C处的梯度方向两侧的点是不一定存在的,或者说是一个亚像素(sub pixel)点,而这个不存在的点, 以及这个点的梯度值就必须通过对其两侧的点进行插值来得到。
对于上面的代码,如果|gy|>|gx|,这说明该点的梯度方向更靠近Y轴方向,所以g2和g4则在C的上下,我们可以用下面来说明这两种情况(方向相同和方向不同):
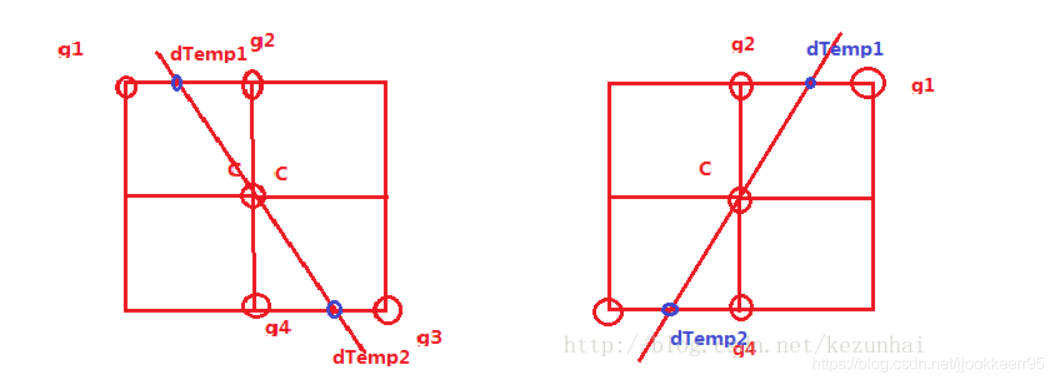
上图中,C表示中心位置点,斜的直线表示梯度方向(非极大值抑制是在梯度方向上的极大值),左边的一副表示gy与gx的方向相同,而右边的这幅这表示gy与gx的方向相反(注意原点在左上角,Y轴向下),而权重则为weight = |gx|/|gy|。
因此则根据此种情况,以左图为例说明。蓝色是梯度方向,g1.g2.g3.g4和dTemp1.dTemp2的位置关系可以表示为:
g2 = pMag[nPos-sz.cx]; // 上一行
g4 = pMag[nPos+sz.cx]; // 下一行
g1 = pMag[nPos+sz.cx+1];
g3 = pMag[nPos-sz.cx-1];
其插值表示则为:
dTemp1 = weight*g1 + (1-weight)*g2;
dTemp2 = weight*g3 + (1-weight)*g4;
这里解释一下插值公式为什么这么写:
weight = fabs(gx)/fabs(gy) = ctan(theta), theta为梯度方向.
上面那个公式变一下就可以变换成:
weight = |dTemp1-g2|/|g1-g2| = |dTemp1-g2|/|C-g2| = ctan(theta);
而从上面的图中的三角形也可以直观的看出。
(只是简单说明一下帮助理解,没有过多考虑正负问题)
同理,我们可以得到|gx|>|gy|的情况,此时说明该点的梯度方向更靠近X轴方向,g2和g4则在水平方向,我们可以用下图来说明该种情况:
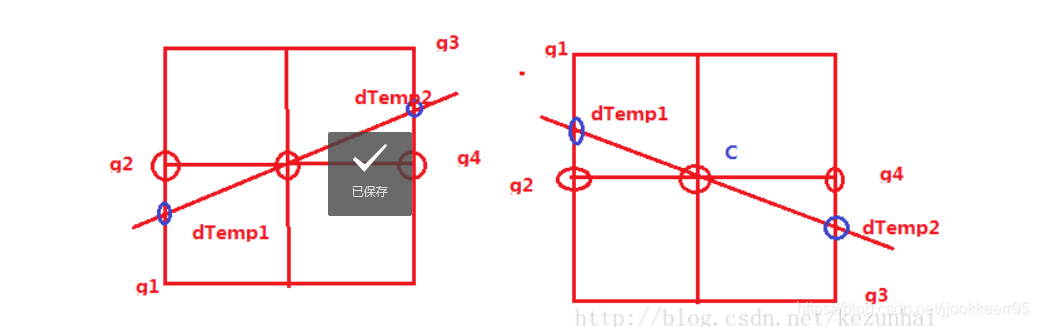
上图中,C表示中心位置点,斜的直线表示梯度方向(非极大值抑制是在梯度方向上的极大值),右边的一副表示gy与gx的方向相同,而左边的这幅这表示gy与gx的方向相反(注意原点在左上角),而权重则为weight = |gy|/|gx|,因此则根据此种情况,其插值表示则为:
dTemp1 = weight*g1 + (1-weight)*g2;
dTemp2 = weight*g3 + (1-weight)*g4;
通过上面的分析,我们可以了解Canny算子中的非极大值抑制之前的准备工作,也即进行必要的插值。插值的原因再啰嗦下:
①由于在Canny算子中采用的简化方法来进行边缘方向的确定,自然图像中边缘梯度方向的不一定沿着该四个方向,因此为了找出在一个像素点上最能吻合其所在梯度方向的两侧的像素值,就必须进行必要的插值;
② 也由于实际数字图像中的像素点是离散的二维矩阵,处在真正中心位置C处的梯度方向两侧的点是不一定存在的,或者说是一个亚像素(sub pixel)点,而这个不存在的点, 以及这个点的梯度值就必须通过对其两侧的点进行插值来得到。
接下来的工作就比较简单了,就是比较中心位置C处dTemp的梯度幅值与两个插值点处的梯度幅值dTemp1和dTemp2的比较,确定是否为极值点,代码如下:
if(dTemp>=dTemp1 && dTemp>=dTemp2)
{
pNSRst[nPos] = 128;
}
else
{
//不可能是边界点
pNSRst[nPos] = 0;
}
到这里,canny算子的非极大值抑制部分就介绍完了。
最后,需要说明的一点:Canny算子中的非极大值抑制与我们在角点检测等场景中所说的非极大值抑制有点细微的差别。Canny算子中的非极大值抑制是沿着梯度方向进行的,即是否为梯度方向上的极值点;而在角点检测等场景下说的非极大值抑制,则是检测中心点处的值是否是某一个邻域内的最大值,是,则保留,否则去除,这种情况下的非极大值抑制比较简单,
如果不清楚可以参考:Alexander Neubeck的论文:Efficient Non-Maximum Suppression。
原作者代码注释和图片解释中有两处错误,在此调整过来了。
11.17日更新:在原作者的基础了添加了位置关系和插值表示的原因
原文链接:https://blog.csdn.net/kezunhai/article/details/11620357