博客

 

一、线性表的链式存储结构

1、线性表链式存储结构定义

线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的。这就意味着，这些数据元素可以存在内存未被占用的任意位置。
以前在顺序结构中，每个数据元素只需要存数据元素信息就可以了。现在链式结构中，除了要存数据元素信息外， 还要存储它的后继元素的存储地址。

因此，为了表示每个数据元素 ai与其直接后继数据元素 ai+1 之间的逻辑关系， 对数据元素ai来说， 除了存储其本身的信息之外，还需存储一个指示其直接后继的信息 (即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域， 把存储直接后继位置的域称为指针域。 指针域中存储的信息称做指针或链。 这两部分信息组成数据元素 ai 的存储映像，称为结点 (Node)。
n 个结点 (ai的存储映像) 链结成一个链表，即为线性表 (a1， a2,…, an) 的链式存储结构，因为链表的每个结点中只包含一个指针域，所以叫做单链表。单链表正是通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起。如图所示：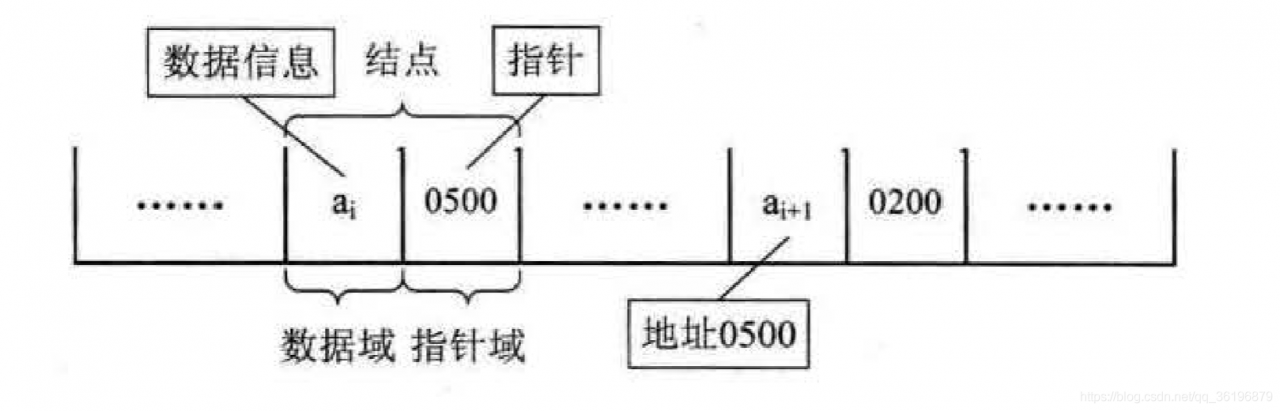

对于线性表来说，总得有个头有个尾，链表也不例外。我们把链表中第一个结点的存储位置叫做头指针，那么整个链表的存取就必须是从头指针开始进行了 。之后的每一个结点，其实就是上一个的后继指针指向的位置。
最后一个， 当然就意味着直接后继不存在了，所以我们规定，线性链表的最后一个结点指针为”空“ (通常用 NULL 或 “^” 符号表示，如图所示)。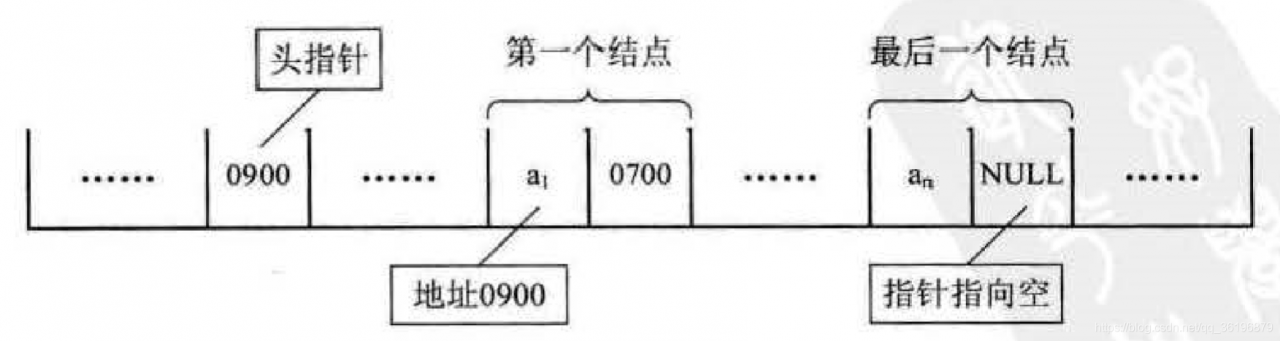

有时，我们为了更加方便地对链表作操作，会在单链表的第一个结点前附设一个结点，称为头结点。头结点的数据域可以不存储任何信息。也可以存储如线性表的长度等附加信息，头结点的指针域存储指向第一个结点的指针。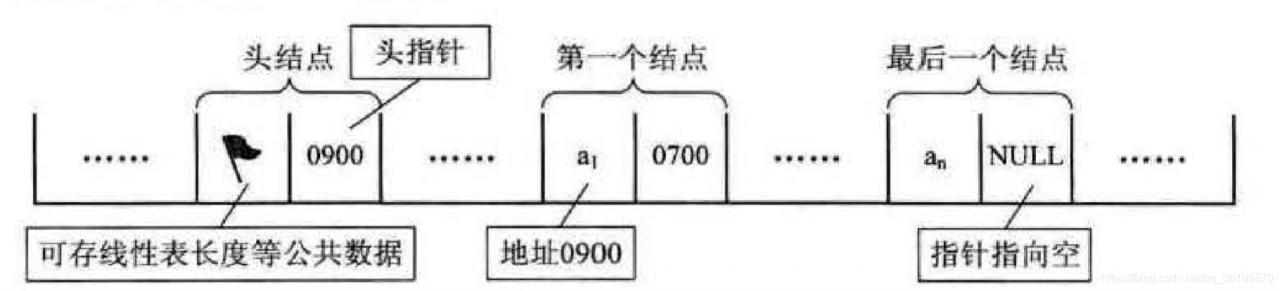

2、头指针与头结点的异同

头指针	头结点
头指针是指链表指向第一个结点的指针，若链表有头结点， 则是指向头结点的指针	头结点是为了操作的统一和方便而设立的，放在第一元素的结点之前，其数据域一般无意义(也可存放链表的长度)
头指针具有标识作用，所以常用头指针冠以链表的名字	有了头结点，对在第一元素结点前插入结点和删除第一结点， 其操作与其它结点的操作就统一了
无论链表是否为空，头指针均不为空。头指针是链表的必要元素	头结点不一定是链表必须元素

二、单链表操作

在线性表的顺序存储结构中，我们要计算任意一个元素的存储位置是很容易的。但在单链表中，由于是逻辑顺序连接的，所以第 i 个元素到底在哪？没办法一开始就知道，必须得从头开始找。因此，对于单链表实现获取第 i 个元素的数据的操作，在算法上，相对要麻烦一些。我们用一个新的链表模型来展示：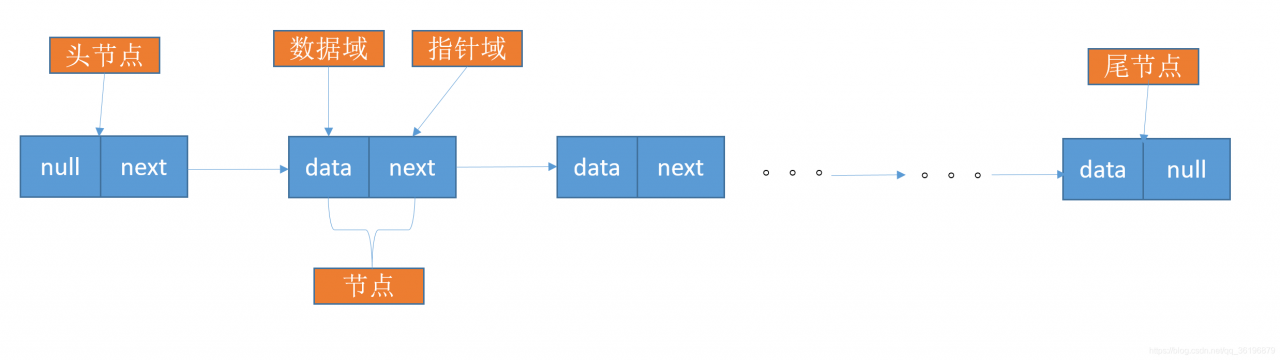

在时间复杂度上看：单链表的查找时间复杂度取决于 i 的位置，当 i=1 时，则不用遍历，第一个就取出数据了，而当 i=n 时则遍历 n-1 次才可以。 因此最坏情况的时间复杂度是 O（n）。
由于单链表的结构中没有定义表长，所以不能事先知道要循环多少次，因此也就不方便使用 for 来控制循环。因此查找元素时主要方法就是 “工作指针后移’，这其实也是很多算法的常用技术。
大家这里是不是感觉链表的查询操作还没有顺序表的操作方便，但是凡事都有两面性，在删除和插入的时候单链表的优势就可以体现的淋漓尽致了，当我们要插入一个数据的时候只需要惊动需要插入位置的前后两个结点，而其它节点是不会被惊动的。
整体操作我们先用示意图表示，然后我们再用代码实现：
第一步创建空链表：
第二步创建头指针与头节点：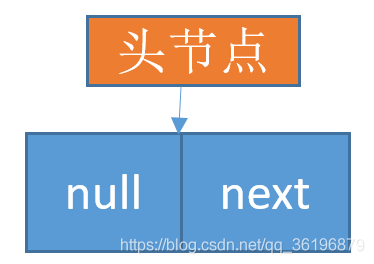

第三步创建尾节点：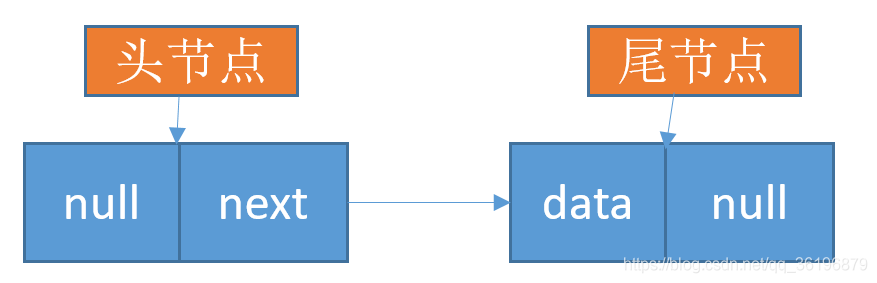

第四步链表中插入元素：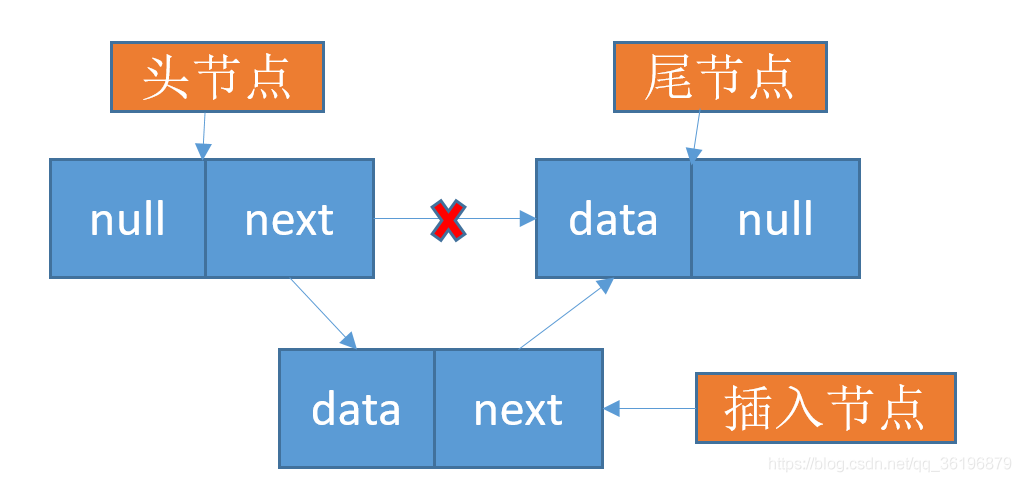

第五步链表中删除元素：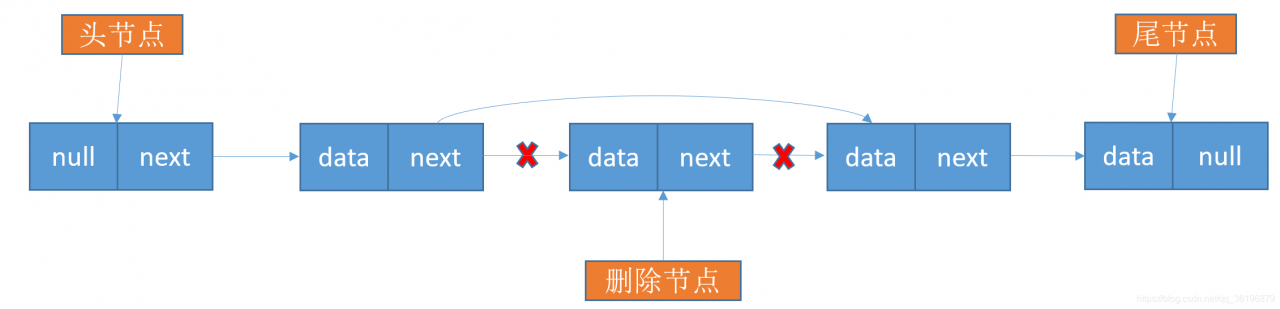

代码实现如下：

public class LinkList<T> {
  private Node<T> headPoint;// 链表的头指针
  private Node<T> head;// 链表的头节点
  private Node<T> tail;// 链表的尾节点


  /**
   * 构建一个节点类
   * 
   * @author YOGA
   *
   * @param <T>
   */
  private static class Node<T> {
    T data;// 泛型数据
    Node<T> next;// 构建指针域，指向下一个节点

    Node(T data) {// 节点的构造函数
      this.data = data;
      this.next = null;
    }
  }

  /**
   * 添加头节点
   */
  public void addHead() {
    this.head = new Node<T>(null);// 创建一个节点赋值给头节点
    this.headPoint = head;// 头指针指向头节点
  }

  /**
   * 添加尾节点
   */
  public void addTail(T data) {
    this.tail = new Node<T>(data);// 创建一个节点赋值给尾节点
    this.head.next = tail;// 头节点的指针域指向尾节点
  }

  /**
   * 在头节点后添加节点
   * 
   * @param data
   */
  public void insertNode(T data) {
    if (this.head == null || this.headPoint == null) {// 如果头节点或者头指针为空，添加头指针与头节点
      addHead();
    } else if (this.tail == null) {// 如果尾节点为空，添加尾节点
      addTail(data);
    } else {
      Node<T> newNodeNext = head.next;// 保存头节点的指针域
      Node<T> newNode = new Node<T>(data);// 创建一个新的节点
      this.head.next = newNode;// 将头节点的指针域指向新节点
      newNode.next = newNodeNext;// 新节点的指针域指向之前头节点指向的指针域
    }
  }

  /**
   * 在指定位置添加节点
   * 
   * @param index
   * @param data
   * @throws Exception
   */
  public void insertNodeByIndex(int index, Node<T> node) throws Exception {
    if (index < 0 || index > length()) {// 判断新插入的位置是否正确
      throw new Exception("插入的位置不合法");
    }
    int length = 1;// 遍历的节点长度
    Node<T> temp = head;// 可移动的指针
    while (head.next != null) {// 遍历单链表
      if (index + 1 == length++) {// 判断是否到达指定位置。
        // 注意，我们的temp代表的是当前位置的前一个结点。
        // 插入操作。

        node.next = temp.next;
        temp.next = node;
        return;
      }
      temp = temp.next;
    }
  }

  /**
   * 删除指定位置的节点
   * 
   * @param index
   * @throws Exception
   */
  public void deleteNode(int index) throws Exception {
    if (isEmpty()) {// 判断链表是否为空
      throw new Exception("链表为空，不能删除");
    }
    if (index < 0 || index > length() + 1) {// 判断新插入的位置是否正确
      throw new Exception("删除的位置不合法");
    }
    int length = 1;// 遍历的节点长度
    Node<T> temp = head;// 可移动的指针
    while (head.next != null) {// 遍历单链表
      if (index + 1 == length++) {// 判断是否到达指定位置。
        // 注意，我们的temp代表的是当前位置的前一个结点。
        // 删除操作与插入操作差不多，改变前一个节点的指向当前节点的下一个节点

        temp.next = temp.next.next;
        return;
      }
      temp = temp.next;
    }
  }

  /**
   * 判断链表是否为空
   */
  public Boolean isEmpty() {
    return this.headPoint == null;
  }

  /**
   * 获取链表的长度
   * 
   * @return
   */
  public int length() {
    int length = 0;
    Node<T> temp = head;
    while (temp.next != null) {
      length++;
      temp = temp.next;
    }
    return length;
  }

  public T getValue(int i) {// 得到结点值
    Node<T> node = head.next;
    int j = 0;
    while (node != null && j < i) {
      node = node.next;
      j++;
    }
    return node.data;
  }

  public static void main(String args[]) throws Exception {
    int i = 1;
    LinkList<Integer> list = new LinkList<Integer>();
    list.addHead();
    list.addTail(i++);
    list.insertNode(i++);
    list.insertNode(i++);
    list.insertNode(i++);
    list.insertNodeByIndex(2, new Node<Integer>(i++));
    for (int j = 0; j < list.length(); j++) {
      System.out.println(list.getValue(j));
    }
    System.out.println("length:" + list.length());
    list.length();
    list.deleteNode(3);
    for (int j = 0; j < list.length(); j++) {
      System.out.println(list.getValue(j));
    }
    System.out.println("length:" + list.length());
  }
}

这里我们从位置0开始，可插入和删除指定位置的节点，然后插入和删除的节点超过范围会报错，计算的节点长度为除头指针和头节点的有效数据节点。
结果如下：

之前我在参考很多代码的时候发现很多不合理的地方，比如只表示头节点不表示头指针，插入和删除的位置不对应，没有进行异常的判断，我这里都做了相应的处理，如果还有什么问题，请大家指出。谢谢

三、单链表结构与顺序存储结构优缺点

对比项	顺序存储结构	单链表结构
存储分配方式	顺序存储结构用一段连续的存储单元依次存储线性表的数据元素	单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素
查找时间复杂度	顺序存储结构O(1)	单链表O(n)
插入和删除时间复杂度	顺序存储结构需要平均移动表长一半的元素，时间为On)	单链表在找出某位置的指针后，插入和删除时间仅为O(1))
空间性能	顺序存储结构需要预分配存储空间，分大了，浪费，分小了易发生上溢	单链表不需要提前存储空间，只要有就可以分配， 元素个数也不受限制

通过上面的对比，我们可以得出一些经验性的结论:
1、若线性表需要频繁查找，很少进行插入和删除操作时，宜采用顺序存储结构。若需要频繁插入和删除时，宜采用单链表结构。比如说游戏开发中， 对于用户注册的个人信息，除了注册时插入数据外，绝大多数情况都是读取，所以应该考虑用顺序存储结构 。而游戏中的玩家的武器或者装备列表，随着玩家的游戏过程中，可能会随时增加或删除，此时再用顺序存储就不大合适了，单链表结构就可以大展拳脚。当然，这只是简单的类比，现实中的软件开发，要考虑的问题会复杂得多。
2、当线性表中的元素个数变化较大或者根本不知道有多大肘，最好用单链表结构， 这样可以不需要考虑存储空间的大小问题。而如果事先知道线性表的大致长度，比如一年12 个月，一周就是星期一至星期日共七天，这种用顺序存储结构效率会高很多。
还是希望大家根据实际情况综合判断。