UCC25600 芯片设计解读与调试

基本电路结构

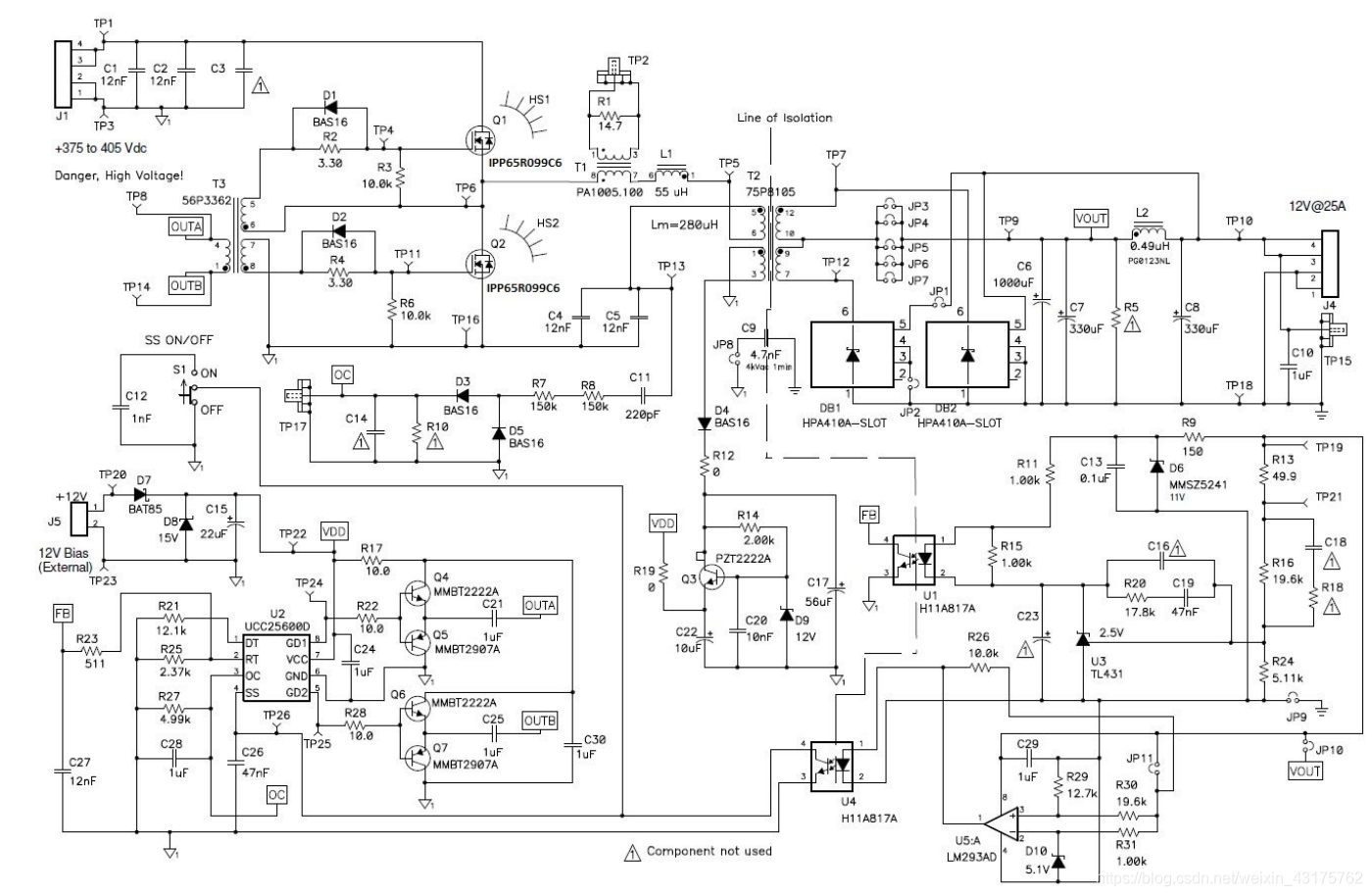
在这里插入图片描述

按照此电路进行配置，即可。

值得注意的是，本电路的输出电压为12V，其相关的电路参数设计也都是基于400V->12V的配置进行设计的。若要改变电路的输入输出值，则以下电路参数需要进行相关的改变：

输出电压反馈的补偿网络
检测谐振电容电压以进行过流保护OC的RC网络
变压器的变比

相关的Python代码稍后奉上，代码将运行两次：

运行现有的电路配置，得到与上图相同的电路参数值（主要是电阻和电容），验证代码原理的正确性；
输入定制的电路配置，得到我们需要的电路参数值。

设计原理：

TL431的反馈回路的设计

UCC25600 输出电压反馈补偿网络的设计

参考文档

基础推导

在这里插入图片描述

图中的Vref规定了直流静态工作点，也即，如果需要得到不同的输出电压，则应当保证在稳态的时候，Rx的分压应当处在Vref附近。

红色框内为modulator，

(

)

G_m(s)

$G_{m} (s)$

；蓝色框内为compensator，

(

)

G_c(s)

$G_{c} (s)$

。

(

)

(

)

(

)

(

)

(

)

G_lp(s) = \frac{V_{out}(s)}{V_r(s)} = G_c(s)G_m(s)

$G_{l} p (s) = \frac{V _{o u t} ( s )}{V _{r} ( s )} = G_{c} (s) G_{m} (s)$

or

(

)

(

)

(

)

(

)

(

)

G_lp(w) = \frac{V_{out}(w)}{V_r(w)} = G_c(w)G_m(w)

$G_{l} p (w) = \frac{V _{o u t} ( w )}{V _{r} ( w )} = G_{c} (w) G_{m} (w)$

(

)

G_m(w) = FBO / FBC

$G_{m} (w) = F B O / F B C$

(

)

G_c(w) = FBC / FBR

$G_{c} (w) = F B C / F B R$

如果只考虑光耦器件的电流传输比CTR(Current Transfer Rate)，则推导出来的补偿网络表达式为：

(

)

G_c(s) = \frac{R_1C_1s+1}{\frac{sR_3R_2C_1}{R_4CTR}} = \frac{\frac{s}{1/R_1C_1}+1}{s/w_1}

$G_{c} (s) = \frac{R _{1} C _{1} s + 1}{\frac{s R _{3} R _{2} C _{1}}{R _{4} C T R}} = \frac{\frac{s}{1 / R _{1} C _{1}} + 1}{s / w _{1}}$

但是，光耦器件并不能只用一个电流传输比表示，它另外一个典型的特征是他的通频带较低，一般认为是10k Hz。所以，它实际上还附带了一个低通滤波器的效果，滤波器的带宽为10k Hz。所以要在表达式上另外加一项

\frac{1}{\frac{s}{w_{opto}}+1}

$\frac{1}{\frac{s}{w _{o p t o}} + 1}$

，其中

∗

w_{opto} = 2\pi*10kHz

$w_{o p t o} = 2 π * 10 k H z$

。故，完整的补偿器的表达式为

(

)

(

)

G_c(s) = \frac{\frac{s}{1/R_1C_1}+1}{s/w_1(\frac{s}{w_{opto}}+1)}

$G_{c} (s) = \frac{\frac{s}{1 / R _{1} C _{1}} + 1}{s / w _{1} ( \frac{s}{w _{o p t o}} + 1 )}$

设计过程Procedure and Results

测量

m

G_m

$G_{m}$

；

1

C_1

$C_{1}$

初始值设定为

1

u

F

0.1 ~ 1uF

$0.11 u F$

(the feedback loop must be stable)
m

G_m

$G_{m}$

measurement with output voltage not in regulation.
Determine initial Gc(w) based on Gm(w) measurement：

最小开关频率规定为70k Hz，则根据经验，穿越频率(crossover frequency)应当低于其1/5，也即7k Hz。

根据测量出的Gm，我们将穿越频率选取为100Hz。（这样做有一个好处，100Hz处的相位基本稳定在0度，所以相位裕度为90度）

因此，设计Gc使得穿越频率为100Hz，选取为100Hz并不是最终的状态，而是为了接下来的调试步骤更加稳定可靠。这一步是为了再次测量Gm，此时电压处在regulation的状态。（对比第二步）
Re-measurement of Gm(w).

渐渐增大输入电压，直到达到期望的输入输出工况。
根据第四步的测量结果，再次设计Gc。
To achieve the crossover frequency of 7 kHz with a minimum 45° phase margin
总体来说，基于UCC25600的LLC设计是一个反复试验的过程。需要结合modulator的硬件测试与compensator的理论计算。

如果能够通过软件扫频得到Gm的bode图？

UCC25600 过流保护RC电路的设计

变压器变比设计

Feature Description

Soft Start

软起动时序
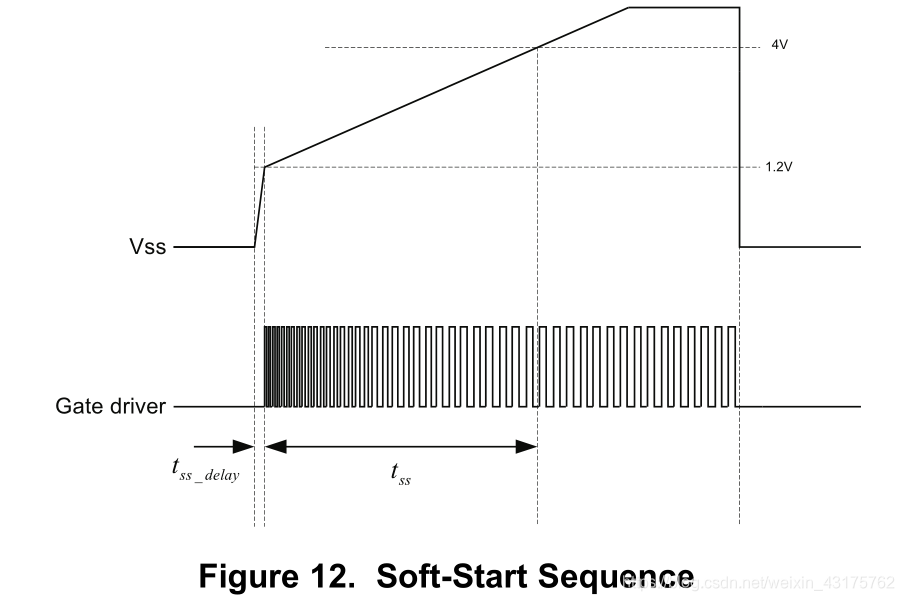
SS 引脚同时也是芯片的ON/OFF引脚，当Vss低于1V的时候, the device is disabled.
当开始启动的时候，如果SS引脚的电压低于1.2V，此时它的输出电流为175uA。因此，上图中的延时

s

s

,

d

e

l

a

y

=

1.2

V

175

u

A

C

s

s

t_{ss, delay} = \frac{1.2V}{175uA}C_{ss}

$t_{s s, d e l a y} = \frac{1 . 2 V}{1 7 5 u A} C_{s s}$
当SS引脚的电压高于1.2V时，此时驱动信号的频率由SS pin的电压和RT引脚的电流共同决定。
s

=

1

2

1

6

n

s

∗

1

A

I

R

T

+

(

1.81

m

A

−

V

s

s

/

2.2

k

Ω

)

+

150

n

s

f_s = \frac{1}{2}\frac{1}{\frac{6ns*1A}{I_{RT}+(1.81mA – V_{ss}/2.2k\Omega)}+150ns}

$f_{s} = \frac{1}{2} \frac{1}{\frac{6 n s * 1 A}{I _{R T} + ( 1 . 8 1 m A - V _{s s} / 2 . 2 k Ω )} + 1 5 0 n s}$
当SS引脚的电压达到4V的时候，输出频率由

R

T

I_{RT}

$I_{R T}$

决定。因此，软起动时间为

s

s

=

2.8

V

5

u

A

C

s

s

t_{ss} = \frac{2.8V}{5uA}C_{ss}

$t_{s s} = \frac{2 . 8 V}{5 u A} C_{s s}$
To ensure reliable operation, the gate drivers restart with GD2 turning high. This prevents uncertainty during system start up.

Overcurrent Protection (OC pin)

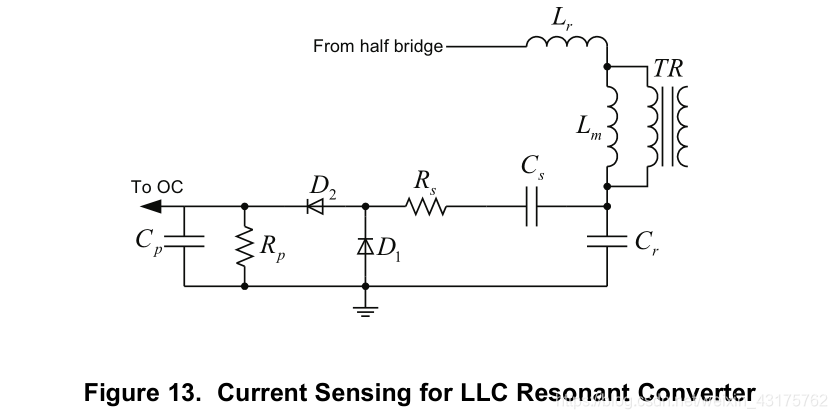
在这里插入图片描述

The general concept of this sensing method is that the ac voltage across the resonant capacitor is proportional to load current. 这种检测过流的原理是基于谐振电压和负载电流是成正比的。
$V_{Cr, peak} = \frac{4}{\pi}nV_o|\frac{jf_nL_nQ_e+1}{f_n^2L_n}| V C r , p e a k = π 4 n V o ∣ f n 2 L n j f n L n Q e + 1 ∣$
电路参数的设计如下表

Name	Function	Design Equation
$R_s R s $	Transfer ac voltage across resonant capacitor into current source	$R_s = \frac{C_{Cr, peak}(max)^2}{2P_{Rs}(max)} R s = 2 P R s ( m a x ) C C r , p e a k ( m a x ) 2 $
$C_s C s $	Blocking dc voltage on resonant capacitor	$C_s = \frac{10}{R_sf_{min}} C s = R s f m i n 1 0 $
$R_p R p $	Load resistor of the current source	$\frac{R_s}{V_{Cr, peak}(max)}\pi V C r , p e a k ( m a x ) R s π$
$C_p C p $	Filter capacitor	$C_p = \frac{10}{R_pf_{min}} C p = R p f m i n 1 0 $

这个电路实现了什么功能呢？
利用二极管、电阻、电容网络实现谐振电容电压的峰值检测。
表格中的function如何理解呢？
- 首先，
  $R_s R s 为什么可以将交流电压转换成一个电流源：电流源和电压源的区别在于，无论何时，电流源的电流都是不变的。在本电路中，通过对比我们可以知道， R s R_s R s 的值相较于后级的并联RC参数是非常大的，也就是说，无论二极管的开通状态如何，前后参数的巨大差异都会使得电路的电流约等于谐振电压除以 R s R_s R s ，也即等效的电流源的幅值为 V C r , p e a k R s \frac{V_{Cr, peak}}{R_s} R s V C r , p e a k $
- 接下来，我们看一下
  $C_s C s 的作用。如果研究电路中的交流量，则 C s C_s C s 的等效阻抗 1 / s C s 1/sC_s 1 / s C s 。将最小开关频率70kHz带入，我们可以求得此时的等效阻抗与 R s R_s R s 差了2个数量级，也即 C s C_s C s 对开关频次的电路量没有影响。但是如果等效出的电流源含有直流量，则 C s C_s C s 的阻抗无穷大，因此，直流量是作用不到后级的RC网络的。$
- 再者，
  $R_p R p 是根据什么选取的呢？由于R从网络和UCC25600芯片连接处的电流很小，也就是说通过二极管传递到后级并联RC网络的电流基本决定了RC网络的电压。由于二极管的整流作用，仅有半个周期的电流可以传递到后级，因此，传递到后级的电流平均值为： I e q u , p k ∗ 1 π = V C r , p e a k R s 1 π I_{equ, pk}*\frac{1}{\pi} = \frac{V_{Cr, peak}}{R_s}\frac{1}{\pi} I e q u , p k ∗ π 1 = R s V C r , p e a k π 1 ，另外我们从UCC25600的数据手册可以得到，OC保护动作开启的电压为1.0V，因此，负载电阻 R p R_p R p 应当能保证最大峰值电压对应的RC网络的电压等于1V，因此， R p R_p R p 的取值应为 R s V C r , p e a k ( m a x ) π \frac{R_s}{V_{Cr, peak}(max)}\pi V C r , p e a k ( m a x ) R s π 。$
- 最后，滤波电容
  $C_p C p 的选取：可以知道，并联RC网络的传递函数为 1 s C \ \ R \frac{1}{sC} \backslash\backslash R s C 1 \ \ R ，其极点为 s = 1 C R s = \frac{1}{CR} s = C R 1 ，为滤除开关频次的电压纹波，将滤波器的转折频率设置为 f s , m i n / 10 f_{s, min}/10 f s , m i n / 1 0 ，则最终可得到对应的电容取值 C = 10 R f m i n C = \frac{10}{Rf_{min}} C = R f m i n 1 0 $

原文链接：https://blog.csdn.net/weixin_43175762/article/details/106836479

基本电路结构

UCC25600 输出电压反馈补偿网络的设计

基础推导

设计过程Procedure and Results

UCC25600 过流保护RC电路的设计

变压器变比设计

Feature Description

Soft Start

Overcurrent Protection (OC pin)

你可能也喜欢