博客

分别求n个数的乘积的所有约数个数以及和。

有分解质因数公式，将每个数都分解质因数，用一个 map 来存每个质数的底数和指数。

p1 的质数可以从零取到 a1, p2 可以取到 a2，以此类推，每个约数由 p1 到 pk 各选一个质数相乘得来，所以约数个数等于 (a1 + 1) * (a2 + 1) …(ak + 1).

将约数之和的公式展开可以发现就是所有约数相加。

求(p1 ^ 0 + p1 ^ 1 + p1 ^ 2 + … + p1 ^ a）的方法：设 t = 1，执行一次 t = p * t + 1 操作，得到 t = p + 1，两次得到 p ^ 2 + p + 1，以此类推，a 次可得到 p ^ a + …+ p ^ 1 + 1，即为答案。

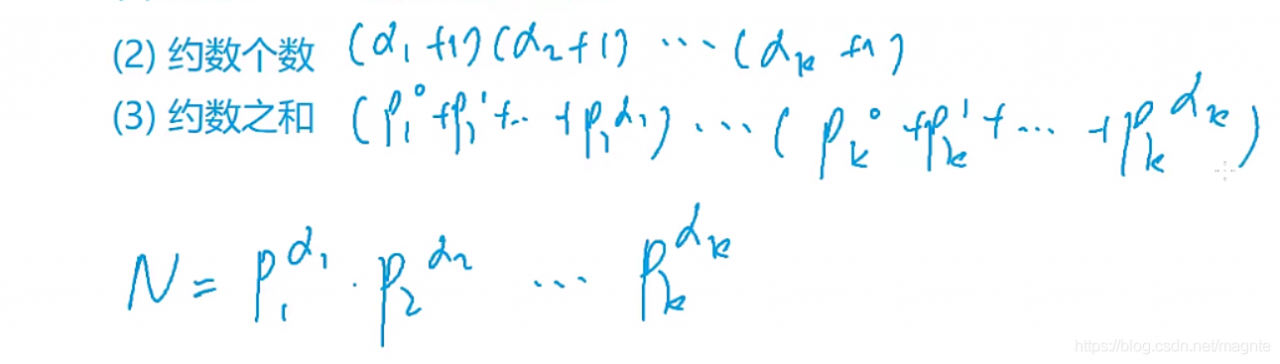
约数个数：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
ll n,x,ans = 1;
unordered_map<int,int>m;

int main()
{
    cin>>n;
    while(n -- )
    {
        cin>>x;
        for(int i = 2; i <= x  /  i; i ++ )//分解质因数
        {
            while(x % i == 0)
            {
                m[i] ++;
                x /= i;
            }
        }
        if(x > 1)
            m[x] += 1;
    }
    for(auto i : m)//套公式
    {
        ans *= (i.second + 1);
        ans %= mod;
    }
    cout<<ans;
    return 0;
}

约数之和：

#include<bits/stdc++.h>
using namespace std;

const long long mod=1e9+7;
typedef long long ll;

int main()
{
    int n;
    ll res = 1;
    unordered_map<int,int>mp;
    cin>>n;

    while(n -- )
    {
        int x;
        cin>>x;
        for(int i = 2; i <= x / i; i ++ )//分解质因数
        {
            while(x % i == 0)
            {
                mp[i] ++ ;
                x /= i;
            }
        }
        if(x > 1)
            mp[x] ++ ;
    }

    for(auto i : mp)//套公式
    {
        ll t = 1;
        while(i.second--)
        {
            t = (t * i.first + 1) % mod;//关键
        }
        res = res * t % mod;
    }

    cout<<res;
    return 0;
}