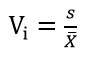统计学之描述性统计(一)
1、描述性统计分析
描述性统计分析主要是对所收集的数据进行分析,得出反映客观现象的各种数量特征的一种分析方法,它包括数据的集中趋势分析、数据离散程度分析、数据的频数分布分析等,描述性统计分析是对数据进一步分析的基础。
2、数据的集中趋势
集中趋势又称 “数据的中心位置”,它是一组数据的代表值。集中趋势的概念就是平均数(Average)的概念,它能够对总体的某一特征具有代表性,表明所研究的对象在一定时间、空间条件下的共同性质和一般水平。
2.1平均数
算术平均数(Arithmetic mean):
统计学术语,是表示一组数据集中趋势的量数,是指在一组数据中所有数据之和再除以这组数据的个数。是数据中心趋势的主要度量指标。对于由n个数据组成的X, 平均值是总和除以总量(N):
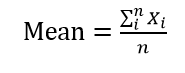
加权平均数
:是不同比重数据的平均数,加权平均数就是把原始数据按照合理的比例来计算。
若n个数据中,X1出现f1次,X2出现f2次,…,Xk出现fk次,那么:
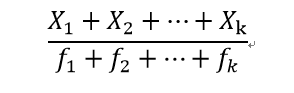
叫做X1,X2,…,Xk的加权平均数。f1,f2,…,fk分别是X1,X2,…,Xk的权,其中f1+f2+…+fk=n。
几何平均数(Geometric mean)
:是n个数据的连乘积的开n次方根,那么对于数据X1,X2,…,Xn的几何平均数为:
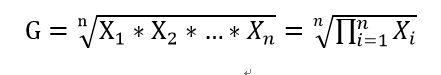
2.2中位数(Median):
代表一个样本、种群或概率分布中的一个数值,其可将数值集合划分为上下两部分。对于有限的数集,可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个,通常取最中间的两个数值的平均数作为中位数。
对于定量数据X,中位数是数值大小位于中间(奇偶总量处理不同)的值:
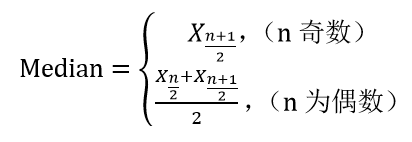
2.3 众数(Mode):
在统计分布上具有明显集中趋势点的数值,代表数据的一般水平(众数可以不存在或多于一个)。另有定义就是一组数据中出现次数最多的数值,叫众数,有时众数在一组数中有好几个。对于定性数据来说,众数是出现次数最多的值。
3、数据的离散程度
数据的离散程度即衡量一组数据的分散程度如何,其衡量的标准和方式有很多,而具体选择哪一种方式则需要依据实际的数据要求进行抉择。主要包括以下方式:
3.1数值型数据:方差、标准差、极差、平均差
3.1.1方差(Variance)和标准差(Standard Deviation)
方差
是在概率论与统计方差衡量随机变量或一组数据时离散程度的变量。统计中的方差(样本方差)是各个数据分别与其平均值之差的平方的和的平均数。
标准差
是方差的算术平方根。它反映的也是数组内个体间的离散程度。
对于一组数据X1,X2,…,Xn,则方差为:
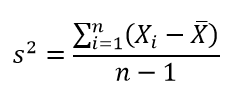
标准差为:
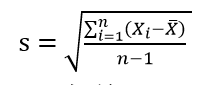
3.1.2极差(Range)
是指一组测量值内最大值与最小值只差,又称范围误差或全距。它是标志值变动的最大范围,它是测定标志变动的最简单的指标。即:
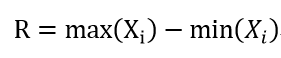
3.1.3平均差
是对一组数据中各个变量与其算术平均数的离差绝对值的算术平均数。它综合反映了总体各变量的变动程度。平均差越大,则表示标志变动度越大,反之则表示标志变动度越小。一组n个数据X1,X2,…,Xn。则平均差为:
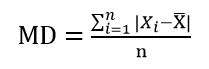
3.2 顺序数据:四分位差
四分位数(Percentage):
是将一组数据由小到大(或由大到小)排序后,用3个点将全部数据分为四等份,与3个点上相对应的变量为四分位数,分别记为Q1(第一四分位数,25%)、Q2(第二四分位数,50%)、Q3(第三四分位数,75%)。
四分位差
是四分位数中的Q3(第三四分位数)到Q1(第一四分位数)之间的距离的一半,一般记为Q。
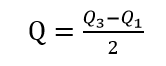
四分位差越小,说明中间的数据越集中;四分位差越大,则意味着中间部分的数据约分散。
3.3分类数据:异众比率(Variation ratio)
异众比率
:又称离异比率或变差比,是指的是非众数的次数与全部变量值总次数的比率,即众数不能代表的那一部分变量值在总体中的比重。
对于一组数据X1,X2,…,Xn,出现的频率分别为f1,f2,…,fk。其中众数出现的次数为fm,则异众比率为:
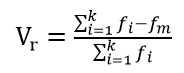
异众比率的作用
是衡量众数对一组数据的代表程度。异众比率越大,说明非众数组的频数占总频数的比重越大,众数的代表性就越差;异众比率越小,说明非众数组的频数占总频数的比重越小,众数的代表性越好。
4、相对离散程度
离散系数
:即变异系数,针对不同数据样本的标准差和方差,因数据衡量单位不同其结果自然无法直接进行对比,为出具一个相同的衡量指标,则进行了离散系数的计算。离散系数为一组数据的标准差与平均数之比。离散系数为: