3D渲染引擎-透视投影(Perspective Projection)
概述
电脑显示器是一个2D平面。如果一个渲染一个3D场景到显示器上,需要对顶点(Vertex)进行投影变换。投影变换会将顶点从相机空间(Camera Space)转换到裁剪空间(Clip Space)。最终通过除法(Perspective Division)将顶点从裁剪空间转换到NDC(Normalized Device Coordinate)。
视锥体(Frustum)

视锥体常出现在计算机3D图形软件或者3D游戏中,用于定义用户的视角。
视锥体有一个近平面(near plane), 一个远平面(far plane),视线经过近平面和远平面形成的夹角被称为Fov(filed of view)。
透视投影矩阵(Perspective Projection Matrix)
约定
-
使用左手坐标系, NDC的取值范围
X ϵ [ − 1 , 1 ] , Y ϵ [ − 1 , 1 ] , Z ϵ [ 0 , 1 ] X\epsilon[-1,1], Y\epsilon[-1,1], Z\epsilon[0,1]
X
ϵ
[
−
1
,
1
]
,
Y
ϵ
[
−
1
,
1
]
,
Z
ϵ
[
0
,
1
]
-
任意一点在Camera Space表示为
P e ( x e , y e , z e , w e ) P_e(x_e,y_e,z_e,w_e)
P
e
(
x
e
,
y
e
,
z
e
,
w
e
)
-
任意一点在Clip Space表示为
P c ( x c , y c , z c , w c ) P_c(x_c,y_c,z_c,w_c)
P
c
(
x
c
,
y
c
,
z
c
,
w
c
)
-
任意一点在NDC中表示为
P n ( x n , y n , z n , w n ) P_n(x_n,y_n,z_n,w_n)
P
n
(
x
n
,
y
n
,
z
n
,
w
n
)
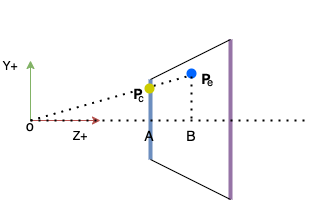
首先求在Camera Space中的一点投影到Clip Space的点,如上图,根据三角形相似我们可以得到如下关系:
O A O B = y c y e {OA\over OB} = {y_c \over y_e}
OB
O
A
=
y
e
y
c
OA其实是原点到近平面(near plane)的距离,记做n。OB其实是点
P e P_e
P
e
的Z值,我们记做
z e z_e
z
e
。所以等式可以转换为
n z e = y c y e {n\over z_e} = {y_c \over y_e}
z
e
n
=
y
e
y
c
由数学公式(6), 我们可以得到
y c y_c
y
c
的值为
y c = n y e z e y_c = {ny_e \over z_e}
y
c
=
z
e
n
y
e
同理我们可以得到
x c x_c
x
c
的值为
x c = n x e z e x_c = {nx_e\over z_e}
x
c
=
z
e
n
x
e
在这里我们先不考虑
z c z_c
z
c
的值,下一步将
x c , y c x_c,y_c
x
c
,
y
c
映射到[-1,1],转换为NDC。假设H为近平面的高度,W为近平面的宽度。原点到近平面的距离记做n。我们可以得到一下关系:
y c y n = H 2 − − > y n = 2 n y c H − − > y n = 2 n y e H z e {y_c \over y_n} = {H \over 2}–> y_n = {2ny_c \over H}–> y_n = {2ny_e \over Hz_e}
y
n
y
c