LBP,全称Local Binary Pattern,局部二值模式,是一种用来描述图像局部特征的算子,具有
灰度不变性
和
旋转不变性
的优点
原始LBP算法
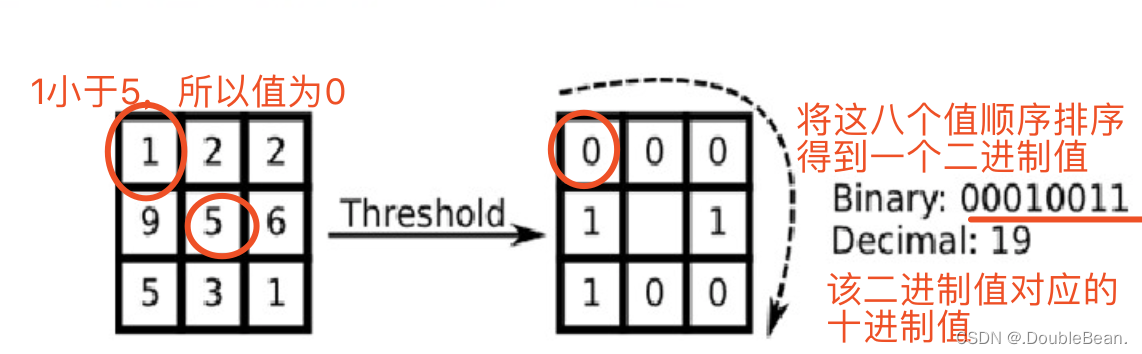
3×3的矩形块,由1个中心像素和它周围的8个邻域像素组成,若相邻像素值大于或等于中间像素值,则值为1,若小于中间像素值则值为0。然后根据顺时针方向读出8个二进制值(不包括中心的那个值),然后转换为十进制数,便可以得到中心像素点的LBP值
假若像素点位于一张图像的上下左右边界,计算的时候,会填充为0
之所以中心像素选择LBP值作为其值,是因为LBP能够反映该中心像素周围区域的纹理信息
# 原始LBP
def LBP(img): # 传入参数的图片已经转为灰度图了
h, w = img.shape[:2]
img_LBP = np.zeros(img.shape, dtype = img.dtype)
for row in range(1, h-1):
for col in range(1, w-1):
center = img[row, col]
LBPtemp = 0
# 比中心像素大的点赋值为1,比中心像素小的点赋值为0,然后将这8位二进制数转换成十进制数
LBPtemp |= (img[row-1,col-1] >= center) << 7
LBPtemp |= (img[row-1,col ] >= center) << 6
LBPtemp |= (img[row-1,col+1] >= center) << 5
LBPtemp |= (img[row ,col+1] >= center) << 4
LBPtemp |= (img[row+1,col+1] >= center) << 3
LBPtemp |= (img[row+1,col ] >= center) << 2
LBPtemp |= (img[row+1,col-1] >= center) << 1
LBPtemp |= (img[row ,col-1] >= center) << 0
img_LBP[row, col] = LBPtemp
return img_LBP

改进算法: 圆形LBP算法
在原始LBP算法中,窗口的半径是固定的,没法满足我们提取不同尺寸和频率纹理的需求,于是提出了圆形LBP算法。改进后的LBP算法允许在半径为R的圆形邻域内有任意多个像素点,
L
B
P
P
R
LBP_P^R
L
B
P
P
R
表示在半径为R的圆内有P个像素点
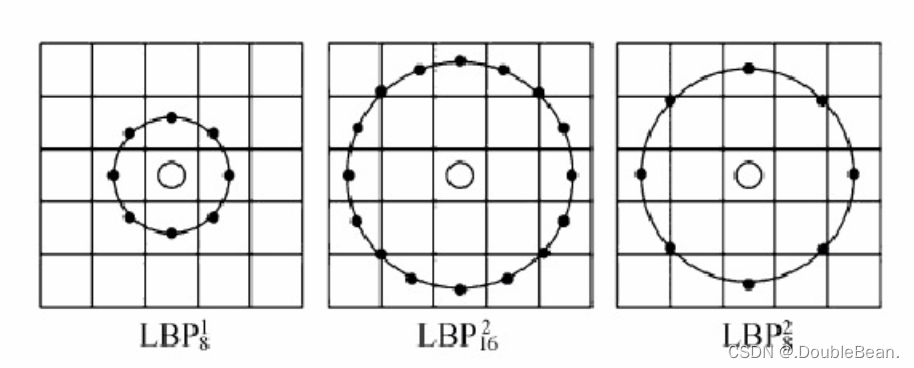
在上图中,第一幅图中圆半径为1,采样点的个数为8;第二幅图中圆半径为2,采样点的个数为16个;第三幅图中圆半径为2,采样点的个数为8
采样点的计算公式如下所示:
x
p
=
x
c
+
R
c
o
s
2
π
p
P
y
p
=
y
c
+
R
s
i
n
2
π
p
P
x_p = x_c + Rcos\frac{2\pi p}{P} \\ y_p = y_c + Rsin\frac{2\pi p}{P}
x
p
=
x
c
+
R
cos
P
2
π
p
y
p
=
y
c
+
R
s
in
P
2
π
p
(x
c
, y
c
)是该窗口的中心坐标,(x
p
, y
p
)是第p个采样点的坐标,p(小写的p)是指第p个采样点,P(大写的P)是指采样点的总数,R为邻域的半径
由于采样点是在圆上分布的,所以无法保证每个采样点的坐标都是整数,对于这样的点,我们需要采用
双线性插值法
来解决
最近邻插值算法和双线性插值算法
好的视频讲解(后面的例子中用了该视频的图片):
https://www.bilibili.com/video/BV1j44y1L7Vo?share_source=copy_web
由于灰度值是定义在整数坐标中的,而通过空间坐标变换 (例如图片缩放,下面的例子就是对图片进行缩放操作) 有可能产生非整数值的坐标,此时就需要根据整数坐标的灰度值去推断非整数值坐标的灰度值,即确定空间位置校正后像素的灰度值,称为灰度插值变换
1. 最近邻插值算法
举个例子,假设原图是一个像素大小为3×3的图片,放大后的图片是一个4×4的大小,原图中的每个像素点都是已知的,这时候我们想知道放大后的图片中坐标为(2,1)这个点的像素值
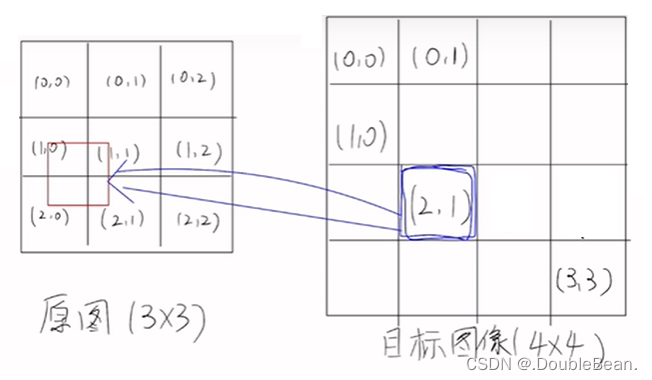
缩放比是3:4,目标图像中坐标为(i, j)像素点按比例对应到原图是
(
i
⋅
3
4
,
j
⋅
3
4
)
(i·\frac{3}{4}, j·\frac{3}{4})
(
i
⋅
4
3
,
j
⋅
4
3
)
,坐标为(2,1)对应的原图是(1.5, 0.75),并非整数,而是落在上图红线框出的矩形中,也就是说放大后的图像中(2, 1)这个点的像素值是和原图中(1, 0)、(1, 1)、(2, 0)、(2, 1)这四个点有关
最近邻域法就是:
在待测像素的四邻域像素中,将距离待求像素最近的邻域像素值赋给待求像素
,距离(1.5, 0.75)最近的点是(2, 1),因为round(1.5)=2,round(0.75)=1,所以目标图像中(2, 1)点处的像素值是原图(2, 1)点处的像素值
当然,图片不一定是正方形,若原图是w·h的图片,放大后图片大小是W·H,现在想知道放大后的图片中(X, Y)的像素值,(x, y)是该点对应回原图的坐标点
宽:
Y
y
=
W
w
\frac{Y}{y} = \frac{W}{w}
y
Y
=
w
W
,得
y
=
r
o
u
n
d
(
Y
⋅
w
W
)
y = round(Y·\frac{w}{W})
y
=
ro
u
n
d
(
Y
⋅
W
w
)
高:
X
x
=
H
h
\frac{X}{x} = \frac{H}{h}
x
X
=
h
H
,得
x
=
r
o
u
n
d
(
X
⋅
h
H
)
x = round(X·\frac{h}{H})
x
=
ro
u
n
d
(
X
⋅
H
h
)
这种方法最为简单,但效果最差,会产生直线边缘的扭曲,存在灰度不连续性,在变化的地方可能出现明显的锯齿状
图像放缩中存在的问题
https://blog.csdn.net/qq_37577735/article/details/80041586
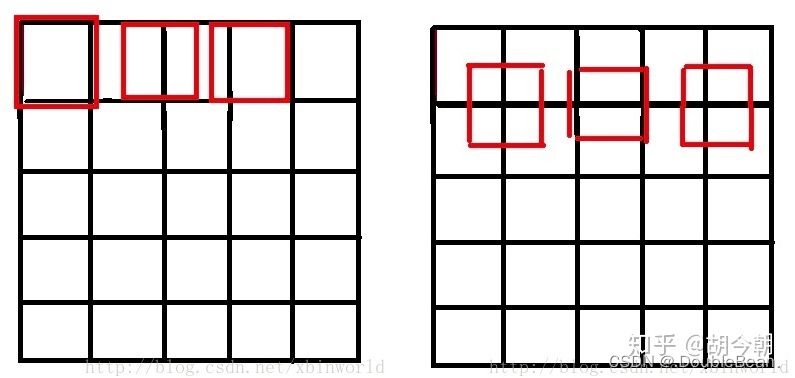
假设原图是3×3,那么中心坐标是(1, 1),目标图像是5×5,那么中心坐标是(2, 2),我们在进行插值映射的时候,肯定是尽可能地希望均匀用到原图像的全部像素信息,最直观的理解就是希望(2, 2)映射到(1, 1)。那我们现在计算一下
x
=
2
×
3
5
=
1.2
x = 2×\frac{3}{5} = 1.2
x
=
2
×
5
3
=
1.2
,即(2, 2)实际映射到原图是(1.2, 1.2),也就是说目标图像的几何中心相对于原始图像的几何中心点是偏右下的,那么整体图像的位置也会发生偏移,为何这么说,其实图像是由一个个的像素点组成,单纯说1个像素点是没有太大的意义的,1个像素点跟相邻像素点的值的渐变或者突变形成图像颜色的渐变或者边界,所以参与计算的点相对往右下偏移会产生相对位置信息的损失
所以为了让目标图像和原图像的几何中心重合,需要修改计算对应坐标点的公式
把
i
n
t
y
=
Y
⋅
w
W
i
n
t
x
=
X
⋅
h
H
int~y = Y·\frac{w}{W} ~~~~~~~~~int~x = X·\frac{h}{H}
in
t
y
=
Y
⋅
W
w
in
t
x
=
X
⋅
H
h
改成:
i
n
t
y
=
(
Y
+
0.5
)
⋅
w
W
−
0.5
i
n
t
x
=
(
X
+
0.5
)
⋅
h
H
−
0.5
int~y = (Y+0.5)·\frac{w}{W}-0.5 ~~~~~~~~~int~x = (X+0.5)·\frac{h}{H}-0.5
in
t
y
=
(
Y
+
0.5
)
⋅
W
w
−
0.5
in
t
x
=
(
X
+
0.5
)
⋅
H
h
−
0.5
上面的例子重新计算一下便是:
x
=
(
2
+
0.5
)
×
3
5
−
0.5
=
1
x = (2 + 0.5) × \frac{3}{5} – 0.5 = 1
x
=
(
2
+
0.5
)
×
5
3
−
0.5
=
1
,目标图像中(2, 2)映射到原图就是(1, 1)了
# 图像缩放
def resize(original_img, new_size):
W, H = new_size # 目标图像宽和高
h, w = original_img.shape[:2] # 原图片宽和高
if h == H and w == W:
return original_img.copy()
scale_y = float(w) / W # y缩放比例
scale_x = float(h) / H # x缩放比例
# 遍历目标图像,插值
new_img = np.zeros((H, W, 3), dtype=np.uint8)
for n in range(3): # 对channel循环
for X in range(H): # 对height循环
for Y in range(W): # 对width循环
# 目标在原图中的坐标(浮点数),使几何中心重合
x = (X + 0.5) * scale_x - 0.5
y = (Y + 0.5) * scale_y - 0.5
if x < 0:
x = 0
if y < 0:
y = 0
# 不考虑几何中心重合直接对应
# x = X * scale_x
# y = Y * scale_y
new_img[X, Y, n] = original_img[int(x), int(y), n]
return new_img
2. 双线性插值算法
在讲双线性插值之前先看一下线性插值
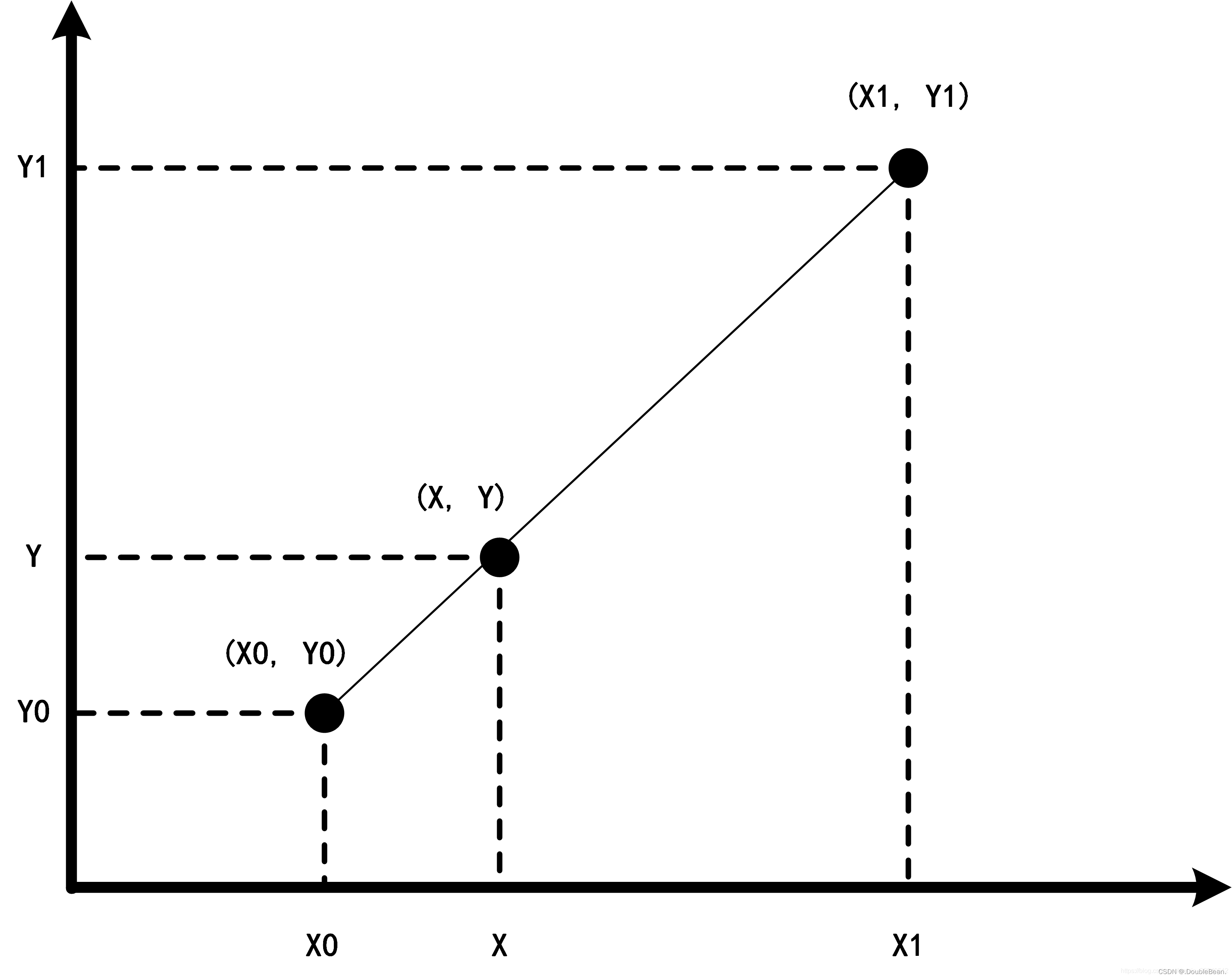
y
=
y
0
+
(
x
−
x
0
)
y
1
−
y
0
x
1
−
x
0
=
x
1
−
x
x
1
−
x
0
y
0
+
x
−
x
0
x
1
−
x
0
y
1
y = y_0 + (x – x_0)\frac{y_1 – y_0}{x_1 – x_0} = \frac{x_1 – x}{x_1 – x_0}y_0 + \frac{x – x_0}{x_1 – x_0}y_1
y
=
y
0
+
(
x
−
x
0
)
x
1
−
x
0
y
1
−
y
0
=
x
1
−
x
0
x
1
−
x
y
0
+
x
1
−
x
0
x
−
x
0
y
1
双线性插值就是线性插值在二维时的推广,在两个方向上做三次线性插值
求插入进来的(x,y)这个点的像素值P
已知它四个邻域点的像素值,即 (x
1
, y
1
)对应的像素值是P
11
:f(x
1
, y
1
);(x
1
, y
2
)对应的像素值是P
12
:f(x
1
, y
2
);(x
2
, y
1
)对应的像素值是P
21
:(x
2
, y
1
);(x
2
, y
2
)对应的像素值是P
22
:(x
2
, y
2
)。由图可知,先用线性插值求出P
1
,P
2
的像素值,再使用一次线性插值便可得到P
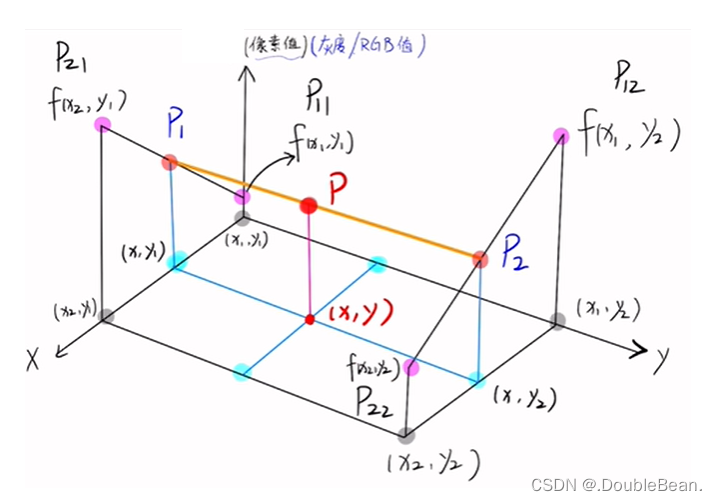
P
1
=
x
2
−
x
x
2
−
x
1
P
11
+
x
−
x
1
x
2
−
x
1
P
21
P
2
=
x
2
−
x
x
2
−
x
1
P
12
+
x
−
x
1
x
2
−
x
1
P
22
P
=
y
2
−
y
y
2
−
y
1
P
1
+
y
−
y
1
y
2
−
y
1
P
2
P_1 = \frac{x_2 – x}{x_2 – x_1}P_{11} + \frac{x – x_1}{x_2 – x_1}P_{21} \\ P_2 = \frac{x_2 – x}{x_2 – x_1}P_{12} + \frac{x – x_1}{x_2 – x_1}P_{22} \\ P = \frac{y_2 – y}{y_2 – y_1}P_{1} + \frac{y – y_1}{y_2 – y_1}P_{2}
P
1
=
x
2
−
x
1
x
2
−
x
P
11
+
x
2
−
x
1
x
−
x
1
P
21
P
2
=
x
2
−
x
1
x
2
−
x
P
12
+
x
2
−
x
1
x
−
x
1
P
22
P
=
y
2
−
y
1
y
2
−
y
P
1
+
y
2
−
y
1
y
−
y
1
P
2
将P
1
和P
2
值代入到P的式子中,然后整理
P
=
P
11
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
2
−
x
)
(
y
2
−
y
)
+
P
21
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
−
x
1
)
(
y
2
−
y
)
+
P
12
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
2
−
x
)
(
y
−
y
1
)
+
P
22
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
x
−
x
1
)
(
y
−
y
1
)
P = \frac{P_{11}}{(x_2 – x_1)(y_2 – y_1)}(x_2 – x)(y_2 – y) + \\ \frac{P_{21}}{(x_2 – x_1)(y_2 – y_1)}(x – x_1)(y_2 – y) + \\ \frac{P_{12}}{(x_2 – x_1)(y_2 – y_1)}(x_2 – x)(y – y_1) + \\ \frac{P_{22}}{(x_2 – x_1)(y_2 – y_1)}(x – x_1)(y – y_1)
P
=
(
x
2
−
x
1
)
(
y
2
−
y
1
)
P
11
(
x
2
−
x
)
(
y
2
−
y
)
+
(
x
2
−
x
1
)
(
y
2
−
y
1
)
P
21
(
x
−
x
1
)
(
y
2
−
y
)
+
(
x
2
−
x
1
)
(
y
2
−
y
1
)
P
12
(
x
2
−
x
)
(
y
−
y
1
)
+
(
x
2
−
x
1
)
(
y
2
−
y
1
)
P
22
(
x
−
x
1
)
(
y
−
y
1
)
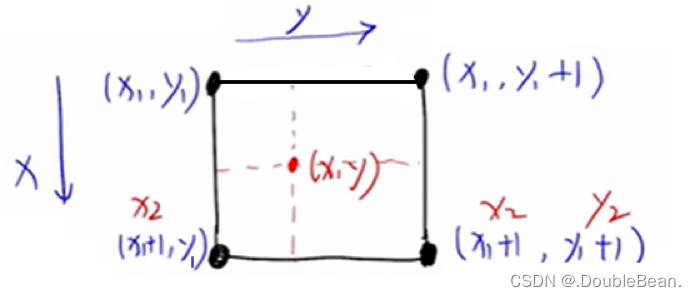
另外,(x, y)的这四个邻域点之间是有关系的,即 x
2
= x
1
+ 1, y
2
= y
1
+ 1,代入上式,可以发现分母就等于1,则上式可以化简成:
P
=
P
11
(
x
2
−
x
)
(
y
2
−
y
)
+
P
21
(
x
−
x
1
)
(
y
2
−
y
)
+
P
12
(
x
2
−
x
)
(
y
−
y
1
)
+
P
22
(
x
−
x
1
)
(
y
−
y
1
)
P
=
[
(
x
2
−
x
)
P
11
+
(
x
−
x
1
)
P
21
(
x
2
−
x
)
P
12
+
(
x
−
x
1
)
P
22
]
[
y
2
−
y
y
−
y
1
]
P
=
[
x
2
−
x
x
−
x
1
]
[
P
11
P
12
P
21
P
22
]
[
y
2
−
y
y
−
y
1
]
P = P_{11}(x_2 – x)(y_2 – y) + P_{21}(x – x_1)(y_2 – y) + P_{12}(x_2 – x)(y – y_1) + P_{22}(x – x_1)(y – y_1) \\ P = \left[ \begin{matrix} (x_2 – x)P_{11} + (x – x_1)P_{21} & (x_2 – x)P_{12} + (x – x_1)P_{22} \end{matrix} \right] \left[ \begin{matrix} y_2 – y \\ y – y_1 \\ \end{matrix} \right] \\ P = \left[ \begin{matrix} x_2 – x & x – x_1 \end{matrix} \right] \left[ \begin{matrix} P_{11} & P_{12} \\ P_{21} & P_{22} \\ \end{matrix} \right] \left[ \begin{matrix} y_2 – y \\ y – y_1 \\ \end{matrix} \right]
P
=
P
11
(
x
2
−
x
)
(
y
2
−
y
)
+
P
21
(
x
−
x
1
)
(
y
2
−
y
)
+
P
12
(
x
2
−
x
)
(
y
−
y
1
)
+
P
22
(
x
−
x
1
)
(
y
−
y
1
)
P
=
[
(
x
2
−
x
)
P
11
+
(
x
−
x
1
)
P
21
(
x
2
−
x
)
P
12
+
(
x
−
x
1
)
P
22
]
[
y
2
−
y
y
−
y
1
]
P
=
[
x
2
−
x
x
−
x
1
]
[
P
11
P
21
P
12
P
22
]
[
y
2
−
y
y
−
y
1
]
当然,该式子还可以写成另一种形式,因为x和y是浮点数,可以写成 (x
1
+u, y
1
+v) 的形式,例如(1.2, 3.4)这个点,那么x
1
=1, u=0.2, y
1
=3, v=0.4
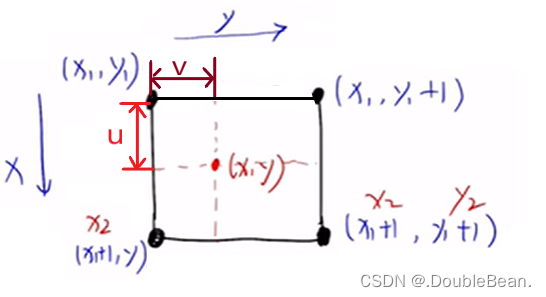
x
2
– x = (x
1
+ 1) – (x
1
+ u) = 1 – u
y
2
– y = (y
1
+ 1) – (y
1
+ v) = 1 – v
x – x
1
= (x
1
+ u) – x
1
= u
故前面的式子有另一种形式
P
=
(
1
−
u
)
(
1
−
v
)
P
11
+
u
(
1
−
v
)
P
21
+
v
(
1
−
u
)
P
12
+
u
v
P
22
P = (1 – u)(1 – v)P_{11} + u(1 – v)P_{21} + v(1 – u)P_{12} + uvP_{22}
P
=
(
1
−
u
)
(
1
−
v
)
P
11
+
u
(
1
−
v
)
P
21
+
v
(
1
−
u
)
P
12
+
uv
P
22
双线性插值的图像放缩的代码如下:
def resize(original_img, new_size):
W, H = new_size # 目标图像宽和高
h, w = original_img.shape[:2] # 原图片宽和高
if h == H and w == W:
return original_img.copy()
scale_y = float(w) / W # y缩放比例
scale_x = float(h) / H # x缩放比例
# 遍历目标图像,插值
new_img = np.zeros((H, W, 3), dtype=np.uint8)
for n in range(3): # 对channel循环
for X in range(H): # 对height循环
for Y in range(W): # 对width循环
# 目标在原图中的坐标(浮点数),使几何中心重合
x = (X + 0.5) * scale_x - 0.5
y = (Y + 0.5) * scale_y - 0.5
if x < 0:
x = 0
if y < 0:
y = 0
# 找到在原图中的四个邻域点,需要知道x1, y1, x2, y2
x_1 = int(np.floor(x))
y_1 = int(np.floor(y)) # floor是向下取整
x_2 = min(x_1 + 1, h - 1)
y_2 = min(y_1 + 1, w - 1) # 防止超出原图的尺寸
# 双线性插值
value0 = (x_2 - x) * original_img[x_1, y_1, n] + (x - x_1) * original_img[x_2, y_1, n]
value1 = (x_2 - x) * original_img[x_1, y_2, n] + (x - x_1) * original_img[x_2, y_2, n]
new_img[X, Y, n] = int((y_2 - y) * value0 + (y - y_1) * value1)
return new_img
圆形LBP代码
现在便可以开始写圆形LBP代码了
步骤:
-
首先我们设置
LB
P
P
R
LBP_P^R
L
B
P
P
R
,即设置参数的值: 半径R和采样点个数P -
用公式
xp
=
x
c
+
R
c
o
s
2
π
p
P
x_p = x_c + Rcos\frac{2\pi p}{P}
x
p
=
x
c
+
R
cos
P
2
π
p
yp
=
y
c
+
R
s
i
n
2
π
p
P
y_p = y_c + Rsin\frac{2\pi p}{P}
y
p
=
y
c
+
R
s
in
P
2
π
p
计算每一个采样点的坐标,因为得到的是浮点数,所以需要用到双线性插值 - 用双线性插值法求出每一个采样点的像素值
- 将窗口中心坐标的像素值作为阈值,每一个采样点的像素值与阈值进行比较,大于或等于阈值设为1,小于阈值设为0,当邻域像素与中心像素比较完后将会得到一串P位二进制数
- 将这P位二进制数转化为十进制数作为窗口中心的LBP值
def circular_LBP(img, R, P): # 参数: 原始图像img,半径R,采样点个数P
h, w = img.shape
img_LBP = np.zeros(img.shape, dtype = img.dtype)
for row in range(R, h-R):
for col in range(R, w-R):
LBP_str = []
for p in range(P): # 遍历全部采样点
# 计算采样点的坐标(浮点数)
x_p = row + R * np.cos(2 * np.pi * p / P)
y_p = col + R * np.sin(2 * np.pi * p / P)
# print(x_p, y_p)
x_1 = int(np.floor(x_p))
y_1 = int(np.floor(y_p)) # floor是向下取整
x_2 = min(x_1 + 1, h - 1)
y_2 = min(y_1 + 1, w - 1) # 防止超出原图的尺寸
# 双线性插值求出这个采样点的像素值
value0 = (x_2 - x_p) * img[x_1, y_1] + (x_p - x_1) * img[x_2, y_1]
value1 = (x_2 - x_p) * img[x_1, y_2] + (x_p - x_1) * img[x_2, y_2,]
temp = int((y_2 - y_p) * value0 + (y_p - y_1) * value1)
# 与窗口中心坐标的像素值进行比较
if temp >= img[row, col]:
LBP_str.append(1)
else:
LBP_str.append(0)
# print(LBP_str)
LBP_str = ''.join('%s' %id for id in LBP_str)
# print(LBP_str, int(LBP_str, 2))
img_LBP[row, col] = int(LBP_str, 2) # 转换为十进制数
return img_LBP
下面的效果图设置的参数是R=3,P=8

LBP算法的旋转不变性
上面的LBP特征具有灰度不变性,但还不具备旋转不变性,解决办法便是
不断旋转圆形邻域得到一系列初始定义的LBP值,取其最小值作为该邻域的LBP值
一个图像的每一个像素点邻域内的像素点的值都是固定的,也就是说与中心像素值比较得到的1或0都是固定的,但因为图像可以发生旋转,这将导致同一个点的LBP值会发生改变,举个例子
假设一个图片全部使用半径为1以及采样点个数为8,并且这8个邻域中已经确定有四个点为0,另外四个点为1,下图便是其中一种
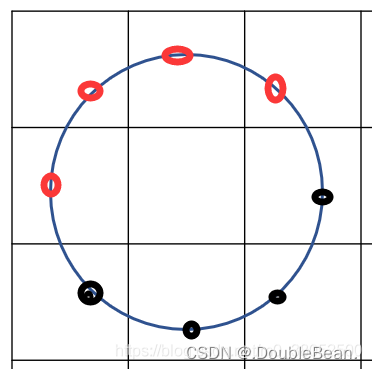
对上图进行旋转,将会产生共8个LBP值,从下图可以看出15是最小值,所以11100001经过旋转处理后的LBP值不再是225,而是15了,这样不管图片怎么旋转,这个点的LBP值都会是15,也就是旋转不变性
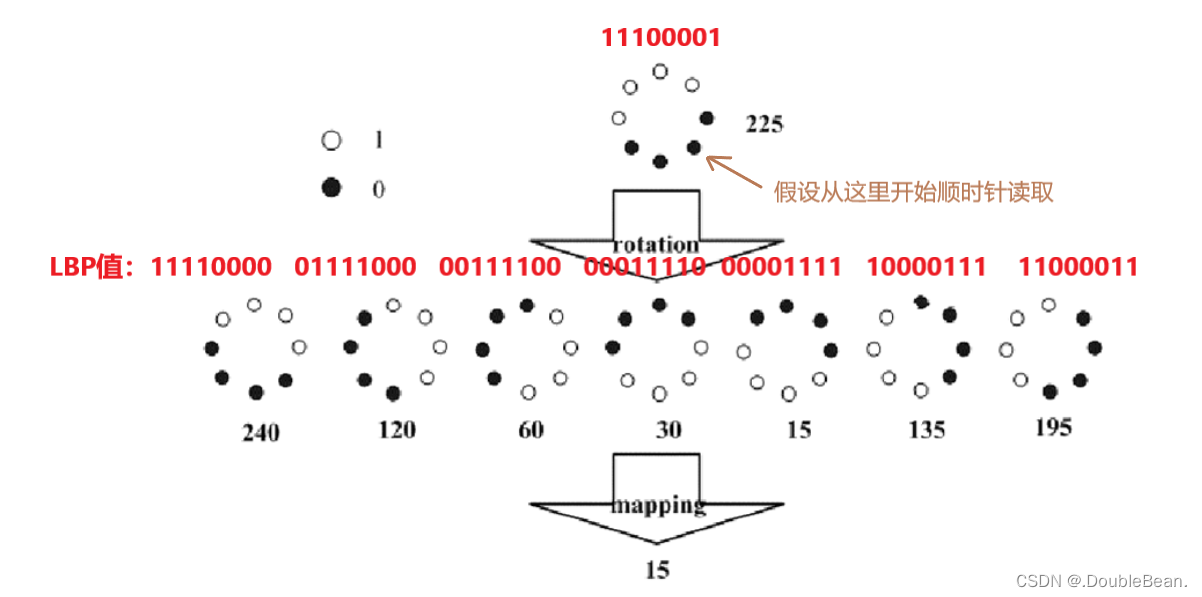
当然,8个采样点中,4个点是0,4个点是1的可能排列情况有
C
8
4
=
70
C_8^4=70
C
8
4
=
70
种。如果只告知了半径为1,采样点个数为8的邻域,并没有告知这8个采样点中有多少个是0,多少个是1,那么每个采样点都有2种结果(要么是0要么是1),所以该圆形LBP将会产生2
8
=256种可能的值
如果对256种模型都做旋转不变性处理,即得到的最小的数作为这种模式的旋转不变LBP值,那么将会得到36种不同的旋转不变性LBP值

为什么最后是36种?(不知道能不能用数学推导证明) 用一段暴力枚举的代码来证明即可
首先用一个列表来记录旋转不变性LBP值,将0-255的数字每一个转成二进制后分别旋转8次,求出最小的十进制数,如果该值不在列表中就添加到列表中
# 证明当采样点个数为8时,旋转不变性LBP值有36种
Data = [] # 用来存放可能的旋转不变性LBP值
for num in range(256):
# print(bin(num)) # '0b...'的形式,因为只需要二进制数,不需要二进制标识符,所以要去掉'0b'
Str = bin(num)[2:].rjust(8, '0') # rjust(len, str)字符向右对齐,用str='0'补齐长度
# 旋转不变性
Min = int(Str, 2) # 转换为十进制数,作为Min的初始值
for i in range(len(Str)):
temp = Str[i::] + Str[:i]
# print(temp, int(temp, 2))
Min = min(int(temp, 2), Min) # 如果有比Min小的值,就更新Min
if Min not in Data: # 如果得到的最小值不在列表中,就添加进列表
Data.append(Min)
# print([bin(m)[2:].rjust(8, '0') for m in Data])
print(len(Data))
print(Data)
代码运行结果:
36
[0, 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 37, 39, 43, 45, 47, 51, 53, 55, 59, 61, 63, 85, 87, 91, 95, 111, 119, 127, 255]
下面便可以开始写旋转不变性LBP的代码
旋转不变性LBP代码的话只需要在圆形LBP代码的基础上增加几行即可
...
# 旋转不变性
Min = int(LBP_str, 2) # 转换为十进制数,作为Min的初始值
for i in range(len(LBP_str)):
t = LBP_str[i::] + LBP_str[:i]
# print(t, int(t, 2))
Min = min(int(t, 2), Min)
img_LBP[row, col] = Min
# print(Min, '\n')

等价LBP
一个LBP算子可以产生不同的二进制模式,对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生2
P
种模式。很显然,随着邻域集内采样点数的增加,二进制模式的种类是急剧增加的。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。例如,将LBP算子用于纹理分类或人脸识别时,常采用LBP模式的统计直方图来表达图像的信息,而较多的模式种类将使得数据量过大,且直方图过于稀疏。因此,需要
对LBP算子的模式进行降维
,使得数据量减少的情况下能最好地代表图像的信息
有实验证明旋转不变性LBP模式的36种情况在一幅图像中分布出现的频率差异较大,有些值出现频率非常高,一些值出现频率却很低。Ojala等认为,在实际图像中,绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此,Ojala将“等价模式”定义为:
当某个局部二进制模式所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该局部二进制模式所对应的二进制就成为一个等价模式类
,如00000000和11111111(0次跳变),00000111(两次跳变,0到1算一次跳变,当环形来看1到0算第二次跳变)和10001111(两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010011(共四次跳变)
在实际图像中,计算出来的LBP值基本都在等价模式中,可达90%以上。等价模式的LBP值个数有一个计算公式: P(P-1)+2 (后面会给出证明),例如采样点个数为8的情况下,等价形式将有 8×(8-1)+2=58 个可能,再加上混合模式这一大类,那么原来的256维将降到 58+1=59 维,这使得特征向量的维度变少了。
注意这只是对灰度不变性LBP进行降维,若对旋转不变性LBP进行降维,那么36种旋转不变性模式将被压缩成9种

先写计算二进制数跳变次数这一函数代码块,因为后面会多次用到
# 计算序列跳变次数
def cal_cnt(Str):
cnt = 0 # 用来存放跳变次数的变量
for i in range(1, len(Str)):
if Str[i-1] != Str[i]: # 如果有变化,计数加1,如果跳变次数为0,1,2就归为等价模式,大于2归为混合模式
cnt += 1
return cnt
当P=8时,圆形LBP模式的256种结果因为等价LBP降维到58种,现在要做的是打一个表用来表示256维如何映射到58维(如果算上混合模式就是59维)
# 创建一个等价LBP表
arr = []
P = 8
for i in range(pow(2, P)):
seq = bin(i)[2:].rjust(P, '0') # 二进制化
cnt = cal_cnt(seq) # 计算该P位二进制数的跳变次数
if cnt <= 2: # 如果跳变次数小于等于2,则依次排序
arr.append(i)
print(len(arr)) # P=8时等价模式
print(arr)
代码运行结果:
从结果可以看到arr列表的长度是58,即256个LBP值中跳变次数小于等于2的只有58个,便是arr中的元素,这些元素对应的索引值便是等价模式的值: 0 ~ 57
58
[0, 1, 2, 3, 4, 6, 7, 8, 12, 14, 15, 16, 24, 28, 30, 31, 32, 48, 56, 60, 62, 63, 64, 96, 112, 120, 124, 126, 127, 128, 129, 131, 135, 143, 159, 191, 192, 193, 195, 199, 207, 223, 224, 225, 227, 231, 239, 240, 241, 243, 247, 248, 249, 251, 252, 253, 254, 255]
旋转不变等价LBP模式可能情况只有9种(如果算上混合模式就是10种)
# 证明旋转不变等价LBP模式只有9种
arr1 = []
P = 8
for i in range(pow(2, P)):
seq = bin(i)[2:].rjust(P, '0') # 二进制化
cnt = cal_cnt(seq) # 计算该P位二进制数的跳变次数
if cnt <= 2:
# 旋转不变性
Min = int(seq, 2) # 转换为十进制数
for j in range(len(seq)):
t = seq[j::] + seq[:j]
# print(t, int(t, 2))
Min = min(int(t, 2), Min)
if Min not in arr1:
arr1.append(Min)
print(len(arr1))
print(arr1)
代码运行结果:
9
[0, 1, 3, 7, 15, 31, 63, 127, 255]
旋转不变等价LBP代码
旋转不变等价LBP步骤基本跟旋转不变LBP一样:
-
首先我们设置
LB
P
P
R
LBP_P^R
L
B
P
P
R
,即设置参数的值: 半径R和采样点个数P -
用公式
xp
=
x
c
+
R
c
o
s
2
π
p
P
x_p = x_c + Rcos\frac{2\pi p}{P}
x
p
=
x
c
+
R
cos
P
2
π
p
yp
=
y
c
+
R
s
i
n
2
π
p
P
y_p = y_c + Rsin\frac{2\pi p}{P}
y
p
=
y
c
+
R
s
in
P
2
π
p
计算每一个采样点的坐标 - 用双线性插值法求出每一个采样点的像素值
- 将窗口中心坐标的像素值作为阈值,每一个采样点的像素值与阈值进行比较,大于阈值设为1,小于阈值设为0,最终会得到一串P位二进制编码
- 计算该二进制数的”01″, “10”跳变次数,若跳变次数大于2,则将窗口中心处的LBP值设为P(P-1)+2=58,即归为混合模式类
- 若跳变次数小于或等于2,那么将这P位二进制数进行旋转,旋转多次后取出最小值,然后取它映射的值 (就是查前面我们已经创建好的那个表,arr用于灰度不变等价LBP,arr1用于旋转不变等价LBP) 作为窗口中心的LBP值,等价模式LBP值范围是[0, 57]
# 旋转不变的等价LBP
def uniform_rotation_LBP(img, R, P): # 参数: 原始图像img,半径R,采样点个数P
h, w = img.shape
img_LBP = np.zeros(img.shape, dtype = img.dtype)
for row in range(R, h-R):
for col in range(R, w-R):
LBP_str = []
for p in range(P): # 遍历全部采样点
# 计算采样点的坐标(浮点数)
x_p = row + R * np.cos(2 * np.pi * p / P)
y_p = col + R * np.sin(2 * np.pi * p / P)
# print(x_p, y_p)
x_1 = int(np.floor(x_p))
y_1 = int(np.floor(y_p)) # floor是向下取整
x_2 = min(x_1 + 1, h - 1)
y_2 = min(y_1 + 1, w - 1) # 防止超出原图的尺寸
# 双线性插值求出这个采样点的像素值
value0 = (x_2 - x_p) * img[x_1, y_1] + (x_p - x_1) * img[x_2, y_1]
value1 = (x_2 - x_p) * img[x_1, y_2] + (x_p - x_1) * img[x_2, y_2,]
temp = int((y_2 - y_p) * value0 + (y_p - y_1) * value1)
# 与窗口中心坐标的像素值进行比较
if temp >= img[row, col]:
LBP_str.append(1)
else:
LBP_str.append(0)
# print(LBP_str)
LBP_str = ''.join('%s' %id for id in LBP_str)
# print(LBP_str, int(LBP_str, 2))
# 等价LBP
count = cal_cnt(LBP_str) # 计算跳变次数
if count > 2:
# 如果变化次数大于2,则该点的LBP值就为 P(P-1)+2,P=8时便是58,被归为混合模式类
img_LBP[row, col] = P * (P - 1) + 2
else: # 符合等价模型
# 旋转不变性
Min = int(LBP_str, 2) # 转换为十进制数
for i in range(len(LBP_str)):
t = LBP_str[i::] + LBP_str[:i]
# print(t, int(t, 2))
Min = min(int(t, 2), Min)
img_LBP[row, col] = arr1.index(Min) # 查表找到该值的索引,便是该点的LBP值
return img_LBP

效果一般,我觉得等价模式本来就是为了降维而生,而旋转不变性LBP维度本身并不高,对于本身就不高的维度降维后,将会丢失掉很多特征信息,所以等价LBP并不适合旋转不变性LBP,而更适合原始LBP以及灰度不变性LBP
下图是将自己写的LBP代码和调库进行比较,不调库的话平均处理一张图像所用时间大约是调库的300倍…

LBPH
LBPH, Local Binary Patterns Histograms,即LBP特征的统计直方图,LBPH将LBP特征与图像的空间信息结合在一起
通过前面任意一种方法都可以获得LBP图像,然后将LBP图像分为几个区域,获取每个区域的LBP编码直方图,其实就是求直方图,只不过以前那种直方图横坐标是像素值的范围 [0, 255],这个是LBP值的范围,原始LBP值范围依旧是 [0, 255],旋转不变LBP值范围是 [0, 35],灰度不变等价LBP值的范围是 [0, 57],旋转不变等价LBP值的范围是 [0, 8] (不包括混合模式这一大类)
然后将各个区域求得的LBP编码直方图拼接起来,就能得到整幅图像的LBP编码直方图
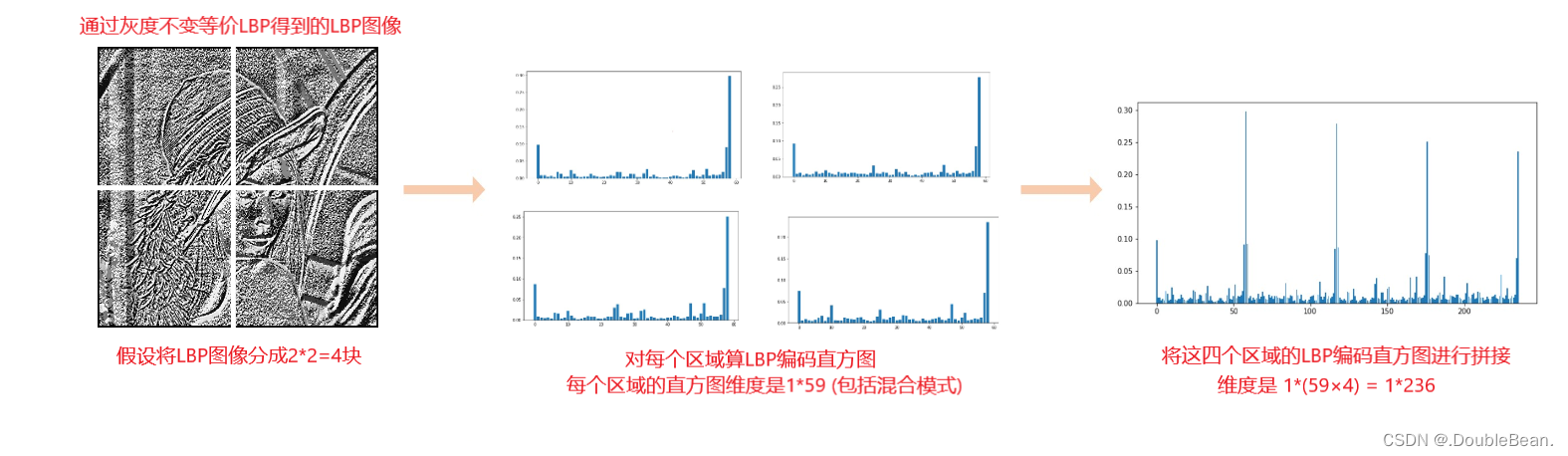
步骤:
- 用上面所说的计算方法得到图像的LBP特征
-
将整个LBP特征图像进行分块,opencv中默认是将LBP特征图像分成8行8列的64块区域,也可以自己设置,假设要将LBP特征图像分成grid_y行grid_x列,即 grid_x·grid_y 块,那么每个区域的宽度和高度便是:
w=
L
B
P
.
c
o
l
s
g
r
i
d
x
w = \frac{LBP.cols}{grid_x}
w
=
g
r
i
d
x
L
BP
.
co
l
s
,
h=
L
B
P
.
r
o
w
s
g
r
i
d
y
h = \frac{LBP.rows}{grid_y}
h
=
g
r
i
d
y
L
BP
.
ro
w
s
-
分别计算每块区域的特征图像的直方图,即统计该区域内所有像素点的分布情况,最终将得到维度是 1 * 2
P
大小的特征向量,若使用等价LBP(包括混合模式这一大类),那得到的是 1 * P(P-1)+3 维度大小的特征向量 -
对每个区域的特征向量进行归一化,然后把所有区域的特征向量按分块的空间顺序一次排列成一行,维度大小为 1 * (2
P
·64),若使用等价模式,则最后的特征向量维度是 1 * ([P(P-1)+3]·64),这个特征向量就能用来表示一张图像 -
计算两幅图像的相似度
Xw
2
(
S
,
M
)
=
∑
i
N
w
i
(
S
i
−
M
i
)
2
S
i
+
M
i
X_w^2(S, M) =\sum_i^N w_i\frac{(S_i – M_i)^2}{S_i + M_i}
X
w
2
(
S
,
M
)
=
∑
i
N
w
i
S
i
+
M
i
(
S
i
−
M
i
)
2
,其中i=1, 2, …, N为图像的某块小区域,w
i
是每块小区域的权重,上式中的分母部分为S
i
+M
i
是考虑到相同人脸在不同照片中的差异性。由公式可知,X
2
值越小表明两幅图越相似
'''
分块计算LBP直方图
参数:
将区域分成grid_x*grid_y个区
maxlength是指不同LBP值的个数,P=8时的圆形LBP值的范围是0-255,则maxlength是256,若使用等价LBP,则maxlength是P*(P-1)+3=59
'''
def cal_LBPH(lbp, grid_x, grid_y, maxlength):
H, W = lbp.shape
width = int(W / grid_x)
height = int(H / grid_y) # 每个小区域的长和宽
Len = width * height
res = []
for i in range(grid_y):
for j in range(grid_x):
src_cell = lbp[i*height : (i+1)*height, j*width : (j+1)*width].ravel() # 获取指定区域
cnt_arr = np.zeros(maxlength, dtype=np.float64).tolist()
for t in range(Len): # 统计区域内不同LBP值的个数
cnt_arr[src_cell[t]] += 1
# print(cnt_arr)
if sum(cnt_arr):
cnt_arr = [x / sum(cnt_arr) for x in cnt_arr] # 归一化
res.extend(cnt_arr)
# print(res)
return res
'''
比较函数: 计算两张图的相似度
参数:
sampleImg: 样本图像矩阵
testImg: 测试图像矩阵
'''
def compare(sampleImg, testImg):
sampleImg_gray = cv.cvtColor(sampleImg, cv.COLOR_BGR2GRAY)
testImg_gray = cv.cvtColor(testImg, cv.COLOR_BGR2GRAY) # 转换成灰度图
'''
# circular_LBP()函数: 灰度不变LBP
LBP_sampleImg = circular_LBP(sampleImg_gray, R = 3, P = 8)
LBP_testImg = circular_LBP(testImg_gray, R = 3, P = 8)
res1 = np.array(cal_LBPH(LBP_sampleImg, grid_x = 8, grid_y = 8, maxlength = 256))
res2 = np.array(cal_LBPH(LBP_testImg, grid_x = 8, grid_y = 8, maxlength = 256)) # 由公式 2^P = 256
print(res1.shape, res2.shape) # 维度是 256*64=16384
'''
# uniform_circular_LBP()函数: 灰度不变等价LBP
LBP_sampleImg = uniform_circular_LBP(sampleImg_gray, R = 3, P = 8) # 对样本图像做灰度不变等价LBP处理
LBP_testImg = uniform_circular_LBP(testImg_gray, R = 3, P = 8) # 对测试图像做灰度不变等价LBP处理
res1 = np.array(cal_LBPH(LBP_sampleImg, grid_x = 8, grid_y = 8, maxlength = 59))
res2 = np.array(cal_LBPH(LBP_testImg, grid_x = 8, grid_y = 8, maxlength = 59)) # 由公式 P * (P-1) + 3 = 59
print(res1.shape, res2.shape) # 维度是 [P*(P-1)+3]*grid_x*grid_y=59*64=3776
# 若直接按照公式写代码会报错,因为分母有为零的数
accuracy = np.sum(np.divide(np.square(res2 - res1), (res1 + res2), out=np.zeros_like(res2), where=(res1 + res2)!=0))
return accuracy
代码运行结果:

从上图可以看到,第一幅图和第二幅图的卡方距离是19.355100474015792,第一幅图和第三幅图的卡方距离是42.508934772556614,所以第一幅图和第二幅图更相似
如果有试过调用库来实现LBPH的话,会发现它是默认划分为8*8=64个区域,如果用灰度不变等价LBP的话,那么最终得到的特征值向量的维度是1 * (59×64) = 1 * 3776,维度还是很大的,所以
需要用PCA对特征向量进行降维
LBPH调库
下面看看LBPH的调库:
cv2.face.LBPHFaceRecognizer_create( [, radius[, neighbors[,grid_x[, grid_y[, threshold]]]]])
- radius:半径值,默认值为1
- neighbors:邻域点的个数,默认采用8邻域,根据需要可以计算更多的邻域点
- grid_x:将LBP特征图像划分为一个个单元格时,每个单元格在水平方向上的像素个数。该参数值默认为8,即将LBP特征图像在行方向上以8个像素为单位分组
- grid_y:将LBP特征图像划分为一个个单元格时,每个单元格在垂直方向上的像素个数。该参数值默认为8,即将LBP特征图像在列方向上以8个像素为单位分组
- threshold:在预测时所使用的阈值。如果大于该阈值,就认为没有识别到任何目标对象
cv2.face_FaceRecognizer.train( src, labels )
- src:训练图像,用来学习的人脸图像
- labels:标签,人脸图像所对应的标签
label, confidence = cv2.face_FaceRecognizer.predict( src )
- src:需要识别的人脸图像
- label:返回的识别结果标签
- confidence:返回的置信度评分。置信度评分用来衡量识别结果与原有模型之间的距离。0表示完全匹配。通常情况下,认为小于50的值是可以接受的,如果该值大于80则认为差别较大
调用LBPH库函数进行识别

上面有五张图片,前面四张当训练集,前面四张中前两张是同一个人,后两张是另一个人,所以标签设置成 labels = [0, 0, 1, 1],最后一张用来做测试
images=[]
images.append(cv.imread("./AR001-1.tif",cv.IMREAD_GRAYSCALE))
images.append(cv.imread("./AR001-2.tif",cv.IMREAD_GRAYSCALE))
images.append(cv.imread("./AR002-1.tif",cv.IMREAD_GRAYSCALE))
images.append(cv.imread("./AR002-2.tif",cv.IMREAD_GRAYSCALE))
predict_image = cv.imread("./AR001-3.tif",cv.IMREAD_GRAYSCALE)
labels=[0,0,1,1]
recognizer = cv.face.LBPHFaceRecognizer_create()
recognizer.train(images, np.array(labels))
label,confidence = recognizer.predict(predict_image)
print("label=",label)
print("confidence=",confidence)
代码运行结果:
从结果可以看到,测试图像识别的结果标签是0,所以判定它与前两张更相似
label= 0
confidence= 60.839928310437784
内容有错或者是代码有错,非常欢迎在评论区中指出
参考资源