SfM（Structure from motion）是一种传统的三维重建的方法，基于多个视角的图像进行3D重建。从时间系列的多幅2D图像中推算3D信息。

稀疏点云重建包含以下步骤:

特征提取与匹配

获取相机的初始参数

求解相机姿态

三角测量得到稀疏点云

捆绑调整,得到精确的相机参数与稀疏点云坐标

三角测量

直接线性变换法

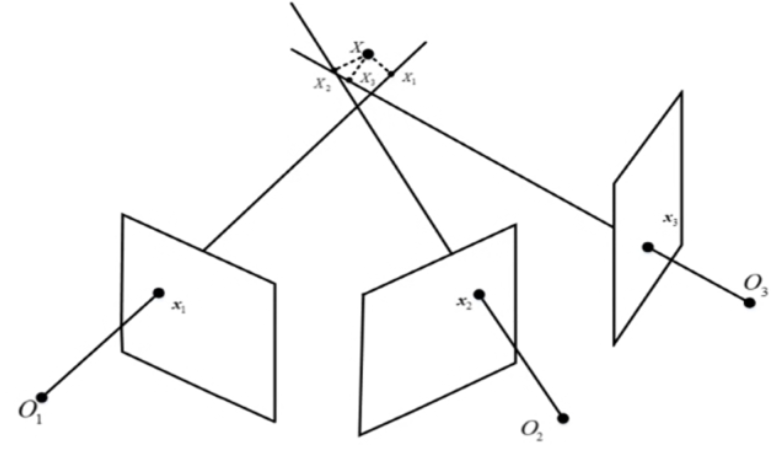
三角测量:已知相机内外参数和同一个三维点对应多个视角像平面上的同名点坐标,恢复三维点的坐标

Alt

已知第i个相机的投影矩阵为

i

P_{i}

$P_{i}$

, 其中

i

K_{i}

$K_{i}$

为第 i 个相机的内参矩阵,

p

i

,

t

i

]

[p_{i}, t_{i}]

$[p_{i}, t_{i}]$

为外参矩阵,第i个相机的投影方程如(1.1)所示:

i

=

K

i

[

P

i

,

t

i

]

=

{

p

i

1

p

i

2

p

i

3

}

(1.1)

P_{i}=K_{i}[P_{i}, t_{i}]=\left\{\begin{matrix} p_{i1}\\p_{i2}\\p_{i3} \end{matrix}\right\}\tag{1.1}

$P_{i} = K_{i} [P_{i}, t_{i}] = ⎩ ⎨ ⎧ p_{i 1} p_{i 2} p_{i 3} ⎭ ⎬ ⎫ (1.1)$

三维点坐标:

i

=

[

x

,

y

,

z

,

1

]

T

X_{i}=[x,y,z,1]^{T}

$X_{i} = [x, y, z, 1]^{T}$

, 在第i个视角的投影的图像(归一化像平面)坐标为:

i

∗

=

[

x

i

,

y

i

,

1

]

T

x_{i}^{*}=[x_{i},y_{i},1]^{T}

$x_{i}^{*} = [x_{i}, y_{i}, 1]^{T}$

根据投影方程:

i

∗

=

P

i

X

(1.2)

x^{*}_{i}=P_{i}X\tag{1.2}

$x_{i}^{*} = P_{i} X (1.2)$

(1.2)两侧同时左叉乘

i

∗

x^{*}_{i}

$x_{i}^{*}$

得:

=

x

i

∗

×

(

P

i

X

)

=

x

i

∗

×

(

{

p

i

1

p

i

2

p

i

3

}

X

)

=

{

x

i

y

i

1

}

×

{

p

i

1

X

p

i

2

X

p

i

3

X

}

(1.3)

0=x^{*}_{i}\times(P_{i}X)=x^{*}_{i}\times(\left\{\begin{matrix} p_{i1}\\p_{i2}\\p_{i3} \end{matrix}\right\}X)=\left\{\begin{matrix}x_{i}\\y_{i}\\1\end{matrix}\right\}\times \left\{\begin{matrix} p_{i1}X\\p_{i2}X\\p_{i3}X \end{matrix}\right\}\tag{1.3}

$0 = x_{i}^{*} \times (P_{i} X) = x_{i}^{*} \times (⎩ ⎨ ⎧ p_{i 1} p_{i 2} p_{i 3} ⎭ ⎬ ⎫ X) = ⎩ ⎨ ⎧ x_{i} y_{i} 1 ⎭ ⎬ ⎫ \times ⎩ ⎨ ⎧ p_{i 1} X p_{i 2} X p_{i 3} X ⎭ ⎬ ⎫ (1.3)$

即:

i

(

p

i

3

X

)

−

P

i

1

X

=

0

y

i

(

p

i

3

X

)

−

P

i

2

X

=

0

x

i

(

p

i

2

X

)

−

y

1

(

P

i

1

X

)

=

0

(1.4)

x_{i}(p_{i3}X)-P_{i1}X=0\\y_{i}(p_{i3}X)-P_{i2}X=0\\x_{i}(p_{i2}X)-y_{1}(P_{i1}X)=0\tag{1.4}

$x_{i} (p_{i 3} X) - P_{i 1} X = 0 y_{i} (p_{i 3} X) - P_{i 2} X = 0 x_{i} (p_{i 2} X) - y_{1} (P_{i 1} X) = 0 (1.4)$

由(1.4)得, 第三个等式与前两个等式线性相关,将其写成矩阵形式如(1.5)所示:

x

i

P

i

3

−

P

i

1

y

i

P

i

3

−

P

i

2

}

X

=

0

(1.5)

\left\{\begin{matrix} x_{i}P_{i3}-P{i1}\\y_{i}P_{i3}-P{i2} \end{matrix}\right\}X=0\tag{1.5}

${x_{i} P_{i 3} - P i 1 y_{i} P_{i 3} - P i 2} X = 0 (1.5)$

已知

=

[

x

i

,

y

i

,

z

i

,

1

]

T

X=[x_{i},y_{i},z_{i},1]^{T}

$X = [x_{i}, y_{i}, z_{i}, 1]^{T}$

, 显然X的自由度为3,由(1.5)可知X点投影的一个视角可以提供两个约束,至少需要两个以上视角才能求解X的三维坐标. 如果同一个三维点X,有N个视角的图像的投影坐标

(

x

1

,

y

1

)

,

.

.

.

(

x

N

,

y

N

)

]

[(x_{1},y_{1}),…(x_{N},y_{N})]

$[(x_{1}, y_{1}), . . . (x_{N}, y_{N})]$

与对应N个相机内外参数,通常使用最小二乘的方式来求解,或者采用Ransac结合最小二乘法求解X的坐标.

X

=

0

A

=

[

x

1

P

13

−

P

11

y

1

P

13

−

P

12

.

.

.

x

i

P

i

3

−

P

i

1

y

i

P

i

3

−

P

i

2

.

.

.

x

N

P

N

3

−

P

N

1

y

N

P

N

3

−

P

N

2

]

,

N

≥

2

(1.6)

AX=0\\A=\begin{bmatrix}x_{1}P_{13}-P_{11}\\y_{1}P_{13}-P_{12}\\…\\x_{i}P_{i3}-P_{i1}\\y_{i}P_{i3}-P_{i2}\\…\\x_{N}P_{N3}-P_{N1}\\y_{N}P_{N3}-P_{N2}\end{bmatrix}, N\ge2 \tag{1.6}

$A X = 0 A = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x_{1} P_{13} - P_{11} y_{1} P_{13} - P_{12} . . . x_{i} P_{i 3} - P_{i 1} y_{i} P_{i 3} - P_{i 2} . . . x_{N} P_{N 3} - P_{N 1} y_{N} P_{N 3} - P_{N 2} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤, N \geq 2 (1.6)$

Ransac算法求解X点的三维坐标算法流程:

1. 计算采样需要的次数

2. 随机采样一对视角,组成A矩阵,对A矩阵进行SVD分解成USV,得到V矩阵的最后一列为最小二乘解,然后将其规范化为

x

i

,

y

i

,

z

i

,

1

]

[x_{i}, y_{i},z_{i}, 1]

$[x_{i}, y_{i}, z_{i}, 1]$

的其次坐标形式

3. 统计内点个数

4. 重复2,3直到满足采样次数,选择内点最多的三维坐标

5. 利用所有内点重新计算三维点的坐标

3D-2D:PnP问题

PnP问题:给定三维坐标点

X

,

Y

,

Z

,

1

]

T

[X,Y,Z,1]^{T}

$[X, Y, Z, 1]^{T}$

与投影到像平面上坐标的点

u

,

v

,

1

]

T

[u,v,1]^{T}

$[u, v, 1]^{T}$

求相机的内外参数K,R,t

直接线性变换法

[

u

v

1

]

=

K

[

R

,

t

]

[

X

Y

Z

1

]

=

[

T

11

T

12

T

13

T

14

T

21

T

22

T

23

T

24

T

31

T

32

T

33

T

34

]

[

X

Y

Z

1

]

=

[

r

1

T

r

2

T

r

3

T

]

X

(2.0)

s\begin{bmatrix}u\\v\\1\end{bmatrix}=K[R, t]\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix}=\begin{bmatrix}T_{11}&T_{12}&T_{13}&T_{14}\\T_{21}&T_{22}&T_{23}&T_{24}\\T_{31}&T_{32}&T_{33}&T_{34}\end{bmatrix}\begin{bmatrix}X\\Y\\Z\\1\end{bmatrix} = \begin{bmatrix}r_{1}^{T}\\r_{2}^{T}\\r_{3}^{T}\end{bmatrix}X\tag{2.0}

$s ⎣ ⎡ u v 1 ⎦ ⎤ = K [R, t] ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎡ T_{11} T_{21} T_{31} T_{12} T_{22} T_{32} T_{13} T_{23} T_{33} T_{14} T_{24} T_{34} ⎦ ⎤ ⎣ ⎢ ⎢ ⎡ X Y Z 1 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎡ r_{1}^{T} r_{2}^{T} r_{3}^{T} ⎦ ⎤ X (2.0)$

式(2.0)中,

u

,

v

,

1

]

T

[u,v,1]^{T}

$[u, v, 1]^{T}$

为像平面上的坐标, s不妨设置为1,表示归一化像平面.K为相机的内参矩阵,

R

,

t

]

[R,t]

$[R, t]$

为相机的外参矩阵,

X

,

Y

,

Z

,

1

]

[X,Y,Z,1]

$[X, Y, Z, 1]$

表示三维空间中点的齐次坐标.将

=

K

[

R

,

t

]

T = K[R, t]

$T = K [R, t]$

记为投影矩阵,其中将T记为

r

1

T

r

2

T

r

3

T

}

\left\{\begin{matrix} r_{1}^{T}\\r_{2}^{T}\\r_{3}^{T} \end{matrix}\right\}

$⎩ ⎨ ⎧ r_{1}^{T} r_{2}^{T} r_{3}^{T} ⎭ ⎬ ⎫$

,

将上式展开,转换成线性方程组的形式如(2.1)所示:

T

r

1

−

X

T

r

3

u

=

0

X

T

r

2

−

X

T

r

3

v

=

0

(2.1)

X^{T}r_{1}-X^{T}r_{3}u=0\\X^{T}r_{2}-X^{T}r_{3}v=0\tag{2.1}

$X^{T} r_{1} - X^{T} r_{3} u = 0 X^{T} r_{2} - X^{T} r_{3} v = 0 (2.1)$

即:

X

1

T

0

−

u

X

1

T

0

X

1

T

−

v

X

1

T

.

.

.

.

.

.

.

.

.

X

N

T

0

−

u

X

N

T

0

X

N

T

−

v

X

N

T

]

[

r

1

r

2

r

3

]

=

0

(2.2)

\begin{bmatrix}X_{1}^{T}&0&-uX_{1}^{T}\\0&X_{1}^{T} &-vX_{1}^{T}\\…&…&…\\X_{N}^{T}&0&-uX_{N}^{T}\\0&X_{N}^{T} &-vX_{N}^{T}\end{bmatrix}\begin{bmatrix}r_{1}\\r_{2}\\r_{3}\end{bmatrix}=0\tag{2.2}

$⎣ ⎢ ⎢ ⎢ ⎢ ⎡ X_{1}^{T} 0 . . . X_{N}^{T} 0 0 X_{1}^{T} . . . 0 X_{N}^{T} - u X_{1}^{T} - v X_{1}^{T} . . . - u X_{N}^{T} - v X_{N}^{T} ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎡ r_{1} r_{2} r_{3} ⎦ ⎤ = 0 (2.2)$

将(2.2)式中的系数矩阵通过SVD分解成USV,找到最小的奇异值对应的特征向量V[:-1]对应该其次方程的最小二乘解,得到投影矩阵T

通过对T矩阵进行QR分解,求取内参矩阵K与外参矩阵[R, t],T(:, 1:3)代表T矩阵的前三列(索引从1开始)

Alt

捆绑调整

捆绑调整:同时对三维点坐标和相机参数进行非线性优化,优化的目标是使得投影的点和观察点的误差越小越好

优化问题描述

在这里插入图片描述

只有

i

j

=

1

x_{ij}=1

$x_{i j} = 1$

也就是第i个点在相机j中可见的时候才需要优化,

i

j

(

C

j

,

X

i

)

u_{ij}(C_{j}, X_{i})

$u_{i j} (C_{j}, X_{i})$

代表投影点是由相机的参数

j

C_{j}

$C_{j}$

和三维空间上的点

j

X_{j}

$X_{j}$

共同决定的,将重投影误差记为

i

j

e_{ij}

$e_{i j}$

,所有优化的参数就是

=

(

C

1

.

.

.

C

m

,

X

1

.

.

.

X

n

)

\theta=(C_{1}…C_{m}, X_{1}…X_{n})

$θ = (C_{1} . . . C_{m}, X_{1} . . . X_{n})$

代表m个相机的内外参数和n个三维点的坐标 ,其中

j

f_{j}

$f_{j}$

代表焦距,

i

j

k_{ij}

$k_{i j}$

代表径向畸变系数,

j

R_{j}

$R_{j}$

代表旋转矩阵,旋转矩阵用一个三维的角轴向量表示,

j

t_{j}

$t_{j}$

表示平移向量,平移向量也是个三维的向量,所以就是1+1+1+3+3=9, 一共m个相机,就是9m,一共n个三维点

i

X_{i}

$X_{i}$

就是3n,

对应的优化问题是一个无约束的非线性最小优化问题.

i

n

g

(

θ

)

=

m

i

n

∣

∣

x

−

f

(

θ

)

∣

∣

2

,

θ

∈

R

n

(3.0)

min g(\theta) = min||x-f(\theta)||^{2}, \theta \in R^{n}\tag{3.0}

$m i n g (θ) = m i n ∣ ∣ x - f (θ) ∣ ∣^{2}, θ \in R^{n} (3.0)$

上述优化问题含有较多待优化的参数,得到的解往往是局部最优解, 因此优化结果依赖于一个较好的初始值.

最速下降法(梯度下降法)

Alt

Alt

牛顿法

在这里插入图片描述

梯度下降法和牛顿法比较:

梯度下降法只用了一阶展开,是当前点局部平面的拟合,而牛顿法是二阶展开,是当前点的局部二次拟合,所以牛顿法收敛速度会更快.

牛顿法需要计算和保存Hessian矩阵,计算量大

Levenberg-Marquardt 算法

原理:

LM算法是一种“信赖阈”的方法,当收敛速度较快时,增大信赖域,使算法趋向于牛顿法;当收敛速度较慢时,减小信赖域,使算法趋向于最速梯度法

优势 :

速度快,只用到一阶矩阵

可以在距离初始值较远处得到最优解

其中

(

θ

)

J(\theta)

$J (θ)$

为雅可比矩阵

在这里插入图片描述

算法流程:

在这里插入图片描述

总结

在这里插入图片描述

sfm点云稀疏重建算法整体流程:

通过sift或者surf求得多对同名点（匹配点）

通过标定或从图像信息中获取相机的初始内参

基于内参矩阵和匹配对, 通过八点法+Ransac求基础矩阵F

基于基础矩阵与内参矩阵求本质矩阵E

基于多个视角的匹配对和相机参数进行三角测量求得三维点坐标,用三维点在相机前的约束从四种情况中挑选出正确的相机姿态R与t

基于匹配对和相机参数进行三角测量,求所有匹配对的三维坐标

基于所有三维坐标与相机参数和匹配对坐标用LM算法进行捆绑调整(非线性优化),得到更精确的三维点坐标与相机内外参数

原文链接：https://blog.csdn.net/weixin_40957452/article/details/120306248

三角测量

直接线性变换法

3D-2D:PnP问题

直接线性变换法

捆绑调整

优化问题描述

最速下降法(梯度下降法)

牛顿法

Levenberg-Marquardt 算法

总结

你可能也喜欢