机器学习中，绕不开的一个概念就是

熵 (Entropy)

，

信息熵

。信息熵常被用来作为一个系统的信息含量的量化指标，从而可以进一步用来作为系统方程优化的目标或者参数选择的判据。在决策树的生成过程中，就使用了熵来作为样本最优属性划分的判据。下面按照本人的理解来系统梳理一下有关熵的概念。

信息量

信息量即信息多少的度量。公式表达如下：

即如果事件


概率越大


，该携带的


信息量越小


；事件


概率越小


，该携带的


信息量越大


。

可以这么理解，太阳从东方升起的概率为1，太阳从西方升起的概率无限接近于0，但是如果有一天太阳从西方升起，那一定是发生了什么明显的自然变化，所以会给我们非常大的信息冲击，给我们提供很多信息量。而东方升起的太阳已经是普遍的经常发生的事情，所以没有什么信息量可言。

信息熵

信息熵是由信息论之父香农提出来的，又叫做香农熵，它用于随机变量的不确定性度量，离散变量的信息熵计算公式如下：

其中n表示随机变量X的取值个数。

让我们回顾一下统计学中的期望，期望的定义就是随机变量的

取值×概率

，比如进行年龄抽查，60岁的概率是0.2，70岁的概率为0.5，80岁的概率为0.3，那么年龄的期望为60*0.2 + 70*0.5 + 80*0.3 = 71岁。

因此可以看出，

信息熵是信息量的期望

。假如对于随机变量x，其取值为1时概率为0.2，则信息量为-log0.2；取值为2的概率为0.5，其信息量为-log0.5；取值为3的概率0.3，其信息量为-log0.3。那么其信息熵就是信息量乘以对应的概率：

– 0.2 * log0.2 -0.5 * log0.5 – 0.3 * log 0.3

针对离散的随机变量的信息熵，有一种比较特殊的情况就是掷硬币，只有正、反两种情况，该种情况（二项分布或者0-1分布）熵的计算可以简化如下：

注意上式还不是交叉熵损失


。

以上是离散的随机变量的情况，对于连续的随机变量，其信息熵的计算公式如下：

在学习信息熵的时候，经常会看到一句话，概率越小，不确定性越大，信息熵越大，信息量越大。其实这句话是不准确的

。

举个例子，事件A发生的概率P(A)= 0.5，那么它的信息熵为H(A) = – 0.5 log(0.5) = 0.5，事件B发生的概率为P(B) = 0.25,那么它的信息熵为H(B)= -0.25log(0.25) = 0.5。可以看到两个事件的信息熵是一样的，并非们前面所说的“概率越小，信息熵越大”。

实际上，信息熵应该是是以


信息接受者


的角度出发的，表示接受者能够接收到的信息量，即


信息熵越大说明我们可以




获取




的信息量越大


。就比如对于事件A，它发生的概率大于事件B的概率，所以事件A本身本身


携带


的信息量小于事件B携带的信息量（这一点是毫无疑问的），但是这不意味者我们能获取的事件B的信息量（信息熵）一定高于事件A，因为毕竟事件B发生的概率很小，只要不发生我们就无法从中获取到信息。



因此，并非概率越小，信息熵越大。



但是反推过去，信息熵高，说明我们能够


获取


的信息量很大，说明这个系统越混乱，这个系统的不确定性大。

对于一个事件X：

• 信息熵↑，不确定性↑，所获取的信息量↑
• 信息熵↓，不确定性↓，所获取的信息量↓

统计分布的距离/相似性计算

• KL散度（Kullback-Leible divergence）
  

KL散度表示


同一个随机变量的两个不同分布间的距离


，假设p(x) 与q(x)是随机变量X的分布，则它们的KL散度为：

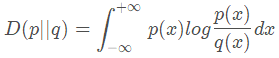
离散情况下，如下：

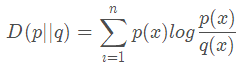
它是从信息熵的角度出发，分析两个分布之间的差异程度，所以又称为


相对熵


。如果两个分布完全相同，则

由上面的公式可以知道，

，即如果要对不同的分布进行比较的话，一定要选好基准的分布。

• JS散度（Jensen-Shannon divergence）
  

JS散度是由KL散度引申而来，主要是为了解决KL散度不对称的问题，它的值一般在(0,1) 之间，公式如下

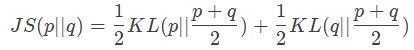
一般JS散度越小，表示分布越相似。

• 交叉熵
  

在博客

常见的损失函数

中，我们从损失函数的角度给出了交叉熵的定义，现在从熵的角度给出。

考虑一种情况，对于一个样本集，存在两个概率分布 p(x) 和q(x)，其中


p(x) 为真实分布，q(x) 为非真实分布（是我们拟合或者说预测的分布）


。基于真实分布 p(x) 表示这个样本集的信息熵如下：

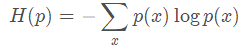
如果我们用非真实分布 q(x)来表示样本集的信息量的话，那么：

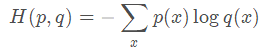
因为其中

为信息量，来自于非真实分布 q(x) ，而对其期望值的计算采用的是真实分布 p(x)，式子中


同时出现了真实分布和预测分布，也是交叉的意义


。

假设某一样本的的类别为C，那么q(x)表示模型预测样本为C类的概率，这很好理解。在机器学习和深度学习的交叉熵损失计算中，我们都知道前面的P(x)是被取值为1的。我认为可以这样理解：根据前面所述P(x)表示样本的真实分布，也就是真实分布中它为C类的概率就为1。这也是为什么在多分类计算交叉熵损失时，我们只需要对每一个样本计算它所属类别的损失，对于其他类别虽然logq(x)是可以计算出来的，但是对应的真实分布为0。

例如：对于二分类问题，当一个样本的标签为real时，其交叉熵损失为-log(q)，q为模型判断样本为real的概率，其真实的分布p=1；当一个样本的标签为fake时，模型判断样本为fake的概率则为1-q，由于其真实标签也为fake，因此前面的p=1，因此其交叉熵损失为-log(1-q)。

• 相对熵与交叉熵的关系
  

对相对熵公式进一步变形为：

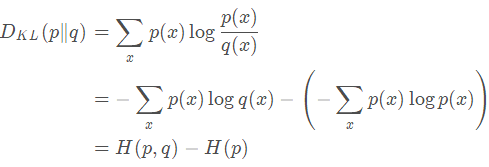
到这一步我们也可以看出，因为

，所以

。

总结起来就是：

KL散度（相对熵） = 交叉熵 – 信息熵

在机器学习中，训练数据的分布已经固定下来，那么真实分布的熵



是一个定值。也就是说交叉熵



越大，相对熵

越大，两个分布的差异越大。

所以交叉熵用来做损失函数就是这个道理，它衡量了真实分布和预测分布的差异性。