目录
1 离散傅里叶级数
1.1 离散傅里叶级数(DFS)
1. 傅里叶变换的几种可能形式:
-
连续时间,连续频率——傅里叶变换(FT)
-
连续时间,离散频率——傅里叶级数(FS)
-
离散时间,连续频率——序列的傅里叶变换(DTFT)
-
离散时间,离散频率——离散傅里叶变换(DFT)
2. 离散傅里叶级数
3. 周期序列的离散傅里叶级数变换对
其中
是周期为N的离散周期信号。
4. DFS与Z变换的关系
周期序列DFS可以看作是
的一个周期x(n)做Z变换,再将Z变换在Z平面单位圆上按等间隔角
抽样而得到。
1.2 离散傅里叶级数的性质
-
线性
-
周期序列的移位
-
调制特性
-
周期卷积
周期卷积与线性卷积的不同之处在于周期卷积仅在一个周期内求和。
2 离散傅里叶变换
2.1 离散傅里叶变换(DFT)
离散傅里叶变换
DFT实际上是DFS的主值,DFT隐含了周期性。x(n)的N点DFT对应x(n)的Z变换在单位圆上N个等间隔点的采样。
2.2 离散傅里叶变换的性质
-
线性
-
对称性:设x(n)为长度为N的实序列
-
循环移位(圆周移位)
-
循环卷积(圆周卷积)
计算过程:补零,周期延拓,翻褶,移位取主值序列,相乘相加。
循环卷积是周期卷积取主值,周期卷积是线性卷积的周期延拓。当
时,可以用长度为L的循环卷积计算两个长度为N的序列的线性卷积。
2.3 频域采样定理
时域抽样造成频域周期延拓,频域抽样造成时域周期延拓。当频域采样点数
时,频域采样X(k)可以不失真地恢复x(n)。进一步可以通过x(n)得到X(z),实现由DFT到ZT的重构,也可以由DTFT与ZT的关系得到傅里叶变换的内插公式。
2.4 离散傅里叶变换的应用
- 混叠现象
- 频谱泄露:时域加窗造成频域的拖尾现象;
- 栅栏效应:可通过增大频域采样的N值,减小频率分辨率来减少栅栏效应;
- 频率分辨率F:决定记录连续信号的最小时间长度;
- 物理频率分辨率:序列的傅里叶变换能够分辨的最小频率;
- 计算频率分辨率:DFT谱线间的距离。
3 快速傅里叶变换
3.1 按时间抽取的基2FFT算法(DIT-FFT)
算法原理:
的对称性、周期性和可约性。
对时间进行奇偶分解,得到
带入DFT公式,得到
由于可约性
得到X(k)的前半部分
考虑到
的的周期性有
考虑到
的对称性有
因此得到X(k)的后半部分
继续分解,最终得到表示算法的蝶形图如下
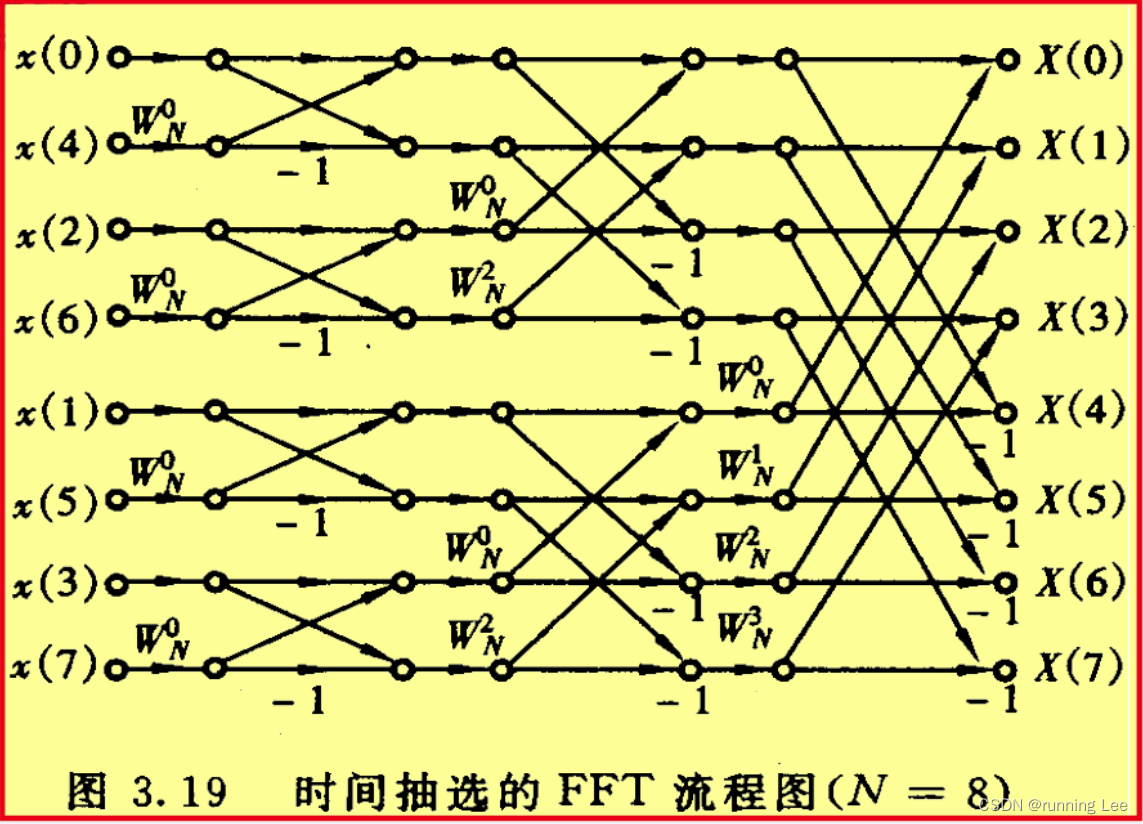
-
同址运算(原位计算):每一组运算结果仍存放在同一组存储器中;
-
变址运算:乱序输入,顺序输出,乱序符合码位倒读规则;
-
FFT的运算量:(M为分解的级数)
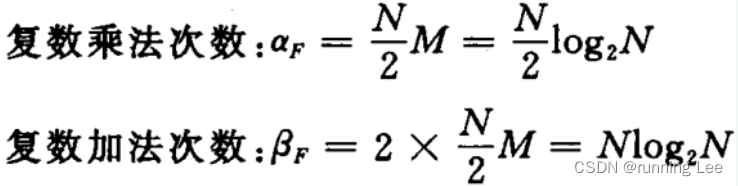
-
N点
DFT的运算量:N^2次复乘,N(N-1)次复加。
3.2 按频率抽取的基2FFT算法(DIF-FFT)
DIF-FFT是将时间前后分,频率偶奇分。与DIT-FFT不同的是,DIT-FFT的计算是先复乘后复加,而DIF-FFT是先复加后复乘。
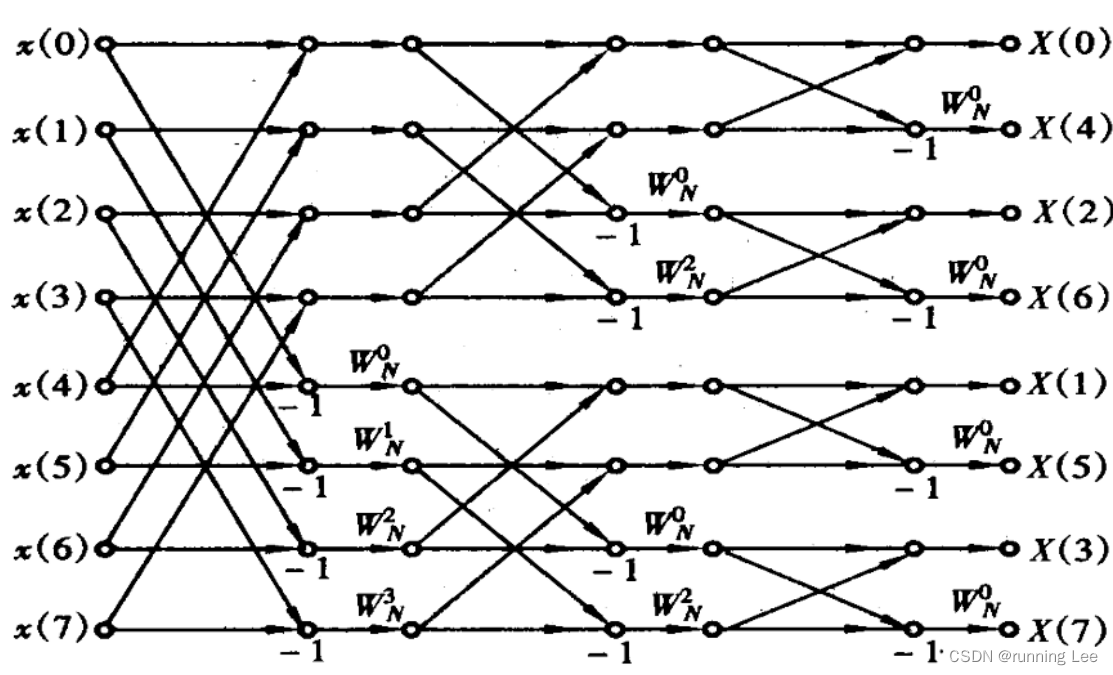
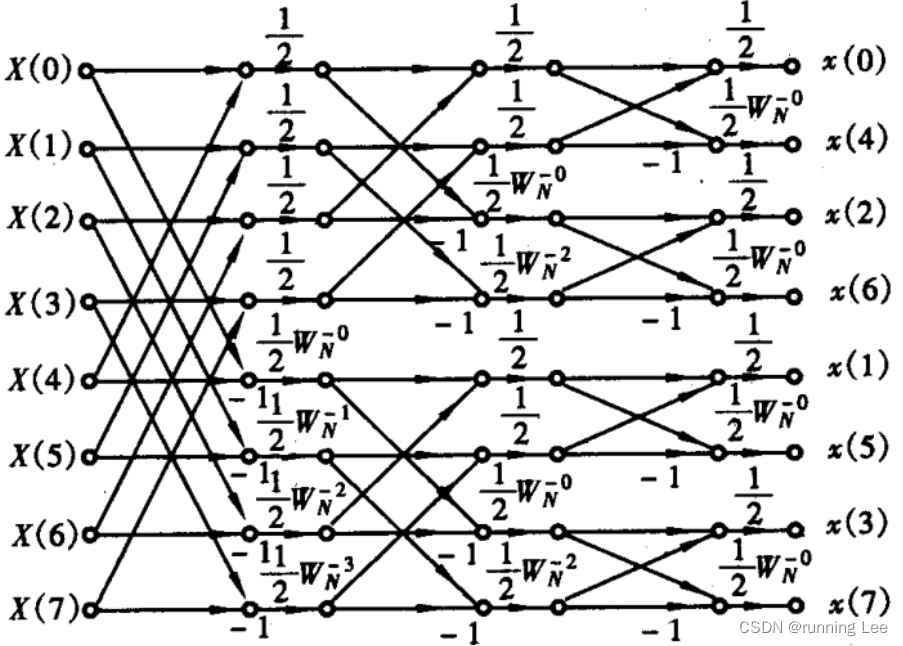
3.3 快速傅里叶反变换
下图所示为按时间抽取的IFFT流程图
3.4 N为合数的FFT算法
如果N不为2的幂,通常有两种处理办法:
-
用补零的方法延长x(n);
-
采用以任意数为基数的FFT算法。
一个N=pq点的DFT可以用p个q点DFT来组成
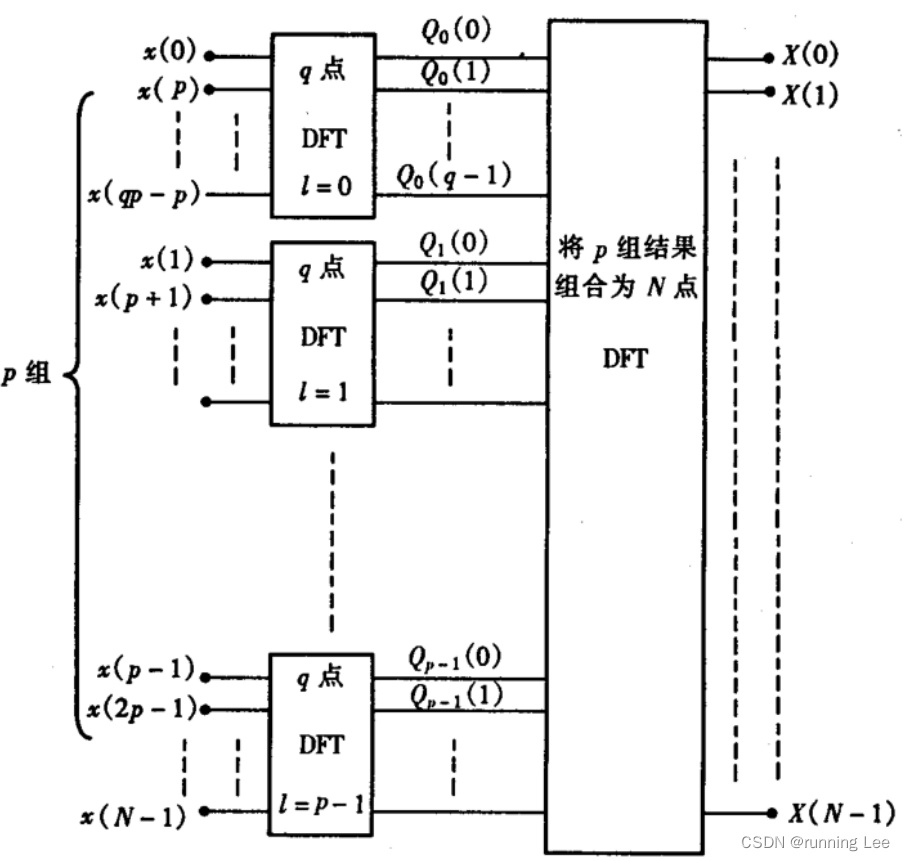
3.5 分段卷积
输入为有限长序列的有限冲激响应(FIR)系统输出可以利用DFT得到,但在实现时存在一定的问题。由于输入序列的长度不确定,无法预先设置DFT的点数进行计算,所以需要先得到所有输入序列的样本,但会导致较大的延迟,这个问题可以利用分段卷积的方法解决。
1. 重叠相加法:将x(n)分成若干长为L的段
-
计算h(n)的N点FFT,N=L+M-1;
-
计算
的N点FFT,N=L+M-1;
-
计算
;
-
求
的N点反变换,得到
;
-
将
的重叠部分相加,得到最后输出
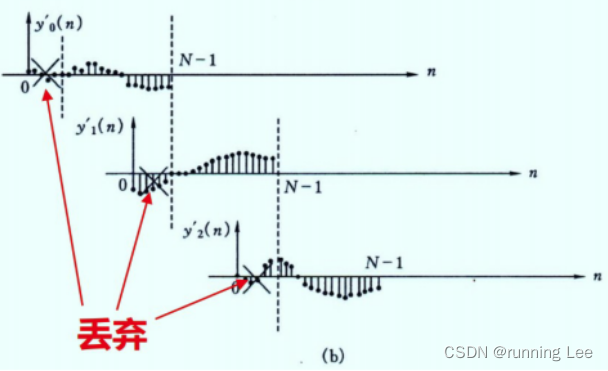
2. 重叠保留法:将x(n)划分为若干长度为N的序列,每段与其前一段重叠M-1个点,计算循环卷积(M<N)并去掉重叠的部分,拼接得到最终结果,如下图所示。
3.6 实序列的FFT算法实现
如果x(n)为实序列,有如下三种处理方式:
1. 把实序列x(n)看作虚部为0的复序列,直接调用FFT;
2. 把两个N点的实序列x(n)和h(n)构造复序列y(n)
对y(n)进行N点FFT,得到
3. x(n)为N点实序列,取x(n)的偶数点和奇数点构造y(n)的实部和虚部
对y(n)做N/2点FFT得到Y(k)
根据DIT-FFT的思想可以得到
由于x(n)为实序列,X(k)具有共轭对称性,则X(k)的另N/2个点的值为