文章目录
COMA 是一种基于 Policy-Based 的多智能体算法,其核心思想是在于 “独立回报分配”。当多个智能体在执行任务时,获得的奖励分数是由所有智能体的行为共同决定的,那么怎么把一个奖励分数合理的分配给每一个智能体呢?这就是 COMA 算法要解决的关键问题。在网络结构上,COMA 沿用了 Actor-Critic 架构,其中 Actor 使用基于 Policy-Based 的 RNN 网络。
1. COMA 解决了什么问题(Motivation)
COMA 是一种解决多智能体强化学习问题的算法,对于大多数多智能体强化学习问题(MARL)都面临着同样一个问题:
信度分配(也叫回报分配)
。
这是指,当多个 Agent 在同时执行任务时,我们应该怎样合理的去评价每一个 Agent 的行为效用,举个例子:
假设我们现在正在训练一个算法模型,使用该算法模型去玩 MOBA 类游戏(DOTA 或者 LOL),算法模型需要同时操控 5 个英雄。在训练过程中遇到了这样一个情况:我方 3 个英雄迎面撞上了敌方 1 个英雄。此时,算法模型控制 1 号英雄和 2 号英雄对敌方英雄发起进攻,但却让 3 号英雄撤退。那么最终,因为 2 打 1 的局面,我方成功击败对方英雄,获得了 10 分的奖励分(Reward),那么我们该怎样为我方的这 3 个英雄进行奖励分配?
在上面案例中,我们很明显能看出,在人数占优势的情况下,算法选择让 1 号和 2 号英雄一起发起进攻是一次正确的尝试,而让 3 号英雄尝试撤退显然就不那么明智了。由于对 1 号和 2 号的正确决策,使得整个指挥策略得到了正向的奖励分(Positive Reward),但显然我们不能直接将这个正向奖励分同时应用到这 3 个英雄上。
我们希望被正确决策的英雄(1 号和 2 号)获得较高的奖励分,而被错误决策的英雄(3 号)获得负的惩罚分,即最后的期望得分可能为:1 号(8分),2 号(8分),3 号(-6分)。
三个英雄的得分总和加起来还是 10 分,只是每个英雄能够按照自己的实际情况获得对应的合理奖励分。
这就是
回报分配
的概念。
为了解决 Individual Reward Assignment 的问题,COMA 引入了一种叫做 “反事实准则(counterfactual baseline)” 的概念,这个概念是整篇论文的重点。
反事实准则提出,每个 agent 应该拥有自己独立的 reward,这样才能知道在这一次的全局行为决策中单个 agent 的 action 贡献是多少。即,通过 counterfactual baseline 来解决 “回报分配” 的问题。
2. COMA 怎么解决独立回报分配问题(Method)
2.1 核心思想 counterfactual baseline 的提出
在第一章节中我们提到,要想成功进行模型训练,我们就需要知道每个 agent 的独立回报究竟是多少。那么单个 agent 的 reward 该怎么去计算呢?
COMA 提出:可以将当前情况下的全局 reward 和将该 agent 行为替换为一个 “默认行为” 后的全局 reward 做差。我们可以这样理解:该回报值其实计算的是 Agent
a
a
a
采取行为
u
u
u
会比采取默认行为
c
a
c_a
c
a
要更好(
D
a
D^a
D
a
> 0)还是更坏(
D
a
D^a
D
a
< 0)。
我们用
D
a
D^a
D
a
来表示单个 Agent 采取行为后的独立回报,计算公式如下:
D
a
=
r
(
s
,
u
)
−
r
(
s
,
(
u
−
a
,
c
a
)
)
D^a = r(s, \textbf{u}) – r(s, (\textbf{u}^{-a}, c_a))
D
a
=
r
(
s
,
u
)
−
r
(
s
,
(
u
−
a
,
c
a
)
)
其中,
u
−
a
\textbf{u}^{-a}
u
−
a
代表联合动作空间除去当前Agent
a
a
a
这一时刻采取的行为。
(
u
−
a
,
c
a
)
(\textbf{u}^{-a}, c_a)
(
u
−
a
,
c
a
)
代表当前Agent
a
a
a
采取”默认行为”
c
a
c_a
c
a
后所有Agent的联合动作空间。
上述
特定agent
的
特定动作
的
reward
(
D
a
D^a
D
a
)就被称为
counterfactual baseline
,COMA 使得每一个 agent 的每一个 action 都会被计算出一个 counterfactual baseline。我们将在后面的章节结合代码来讲解这个 counterfactual baseline 究竟怎么计算。
2.2 算法大框架 —— 基于 AC 框架的 CTDE(Centralized Training Distributed Execution)模式
和主流多智能体强化学习算法一样,COMA 也利用 Center-Critic 和 Actor 来实现 “中心式学习,分布式执行” 的模式。即,在训练阶段输入全局信息给中心式 Critic,通过 中心 Critic 教会 Actor 如何来进行行为决策。
但和传统 AC 或是 QMIX 不一样,COMA 中的 Critic 并不直接估计状态值函数
V
V
V
或是全局总回报
Q
t
o
t
Q_{tot}
Q
t
o
t
,而是去估计一个 agent 在指定状态下所有可执行行为的 Q 值,并通过这些 Q 值完成 counterfactual baseline 的计算。在 2.4 章中我会详细讲解计算过程。
算法网络结构如下:
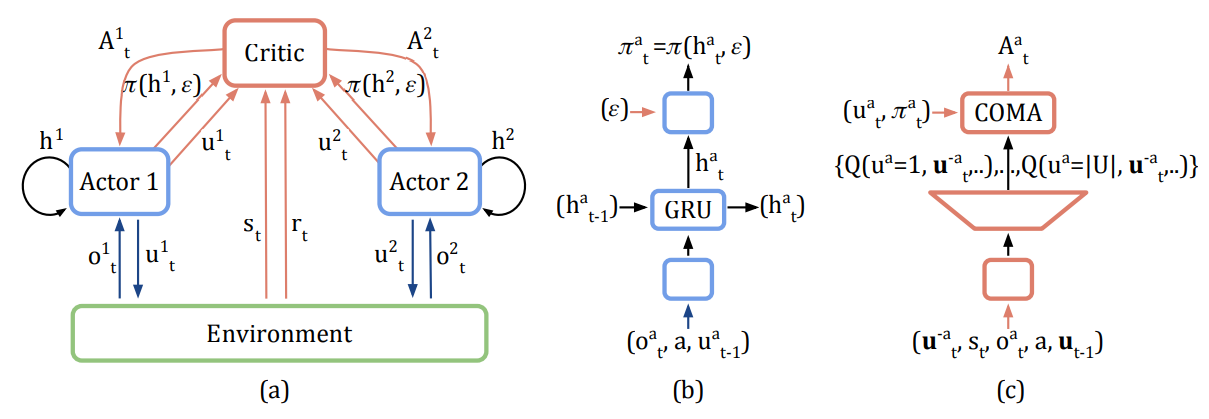
下面我们分别来看看 Actor 和 Critic 的详细设计。
2.3 Actor 网络设计
COMA 中每一个 Agent 都由 RNN 网络控制,在训练时你可以为每一个 Agent 个体都训练一个独立的 RNN 网络,同样也可以所有 Agent 复用同一个 RNN 网络,这取决于你自己的设计。
RNN 网络一共包含 3 层,输入层(MLP)→ 中间层(GRU)→ 输出层(MLP),实现代码如下:
class RNN(nn.Module):
# 所有 Agent 共享同一网络, 因此 input_shape = obs_shape + n_actions + n_agents(one_hot_code)
def __init__(self, input_shape, args):
super().__init__()
self.fc1 = nn.Linear(input_shape, args.rnn_hidden_dim)
self.rnn = nn.GRUCell(args.rnn_hidden_dim, args.rnn_hidden_dim) # GRUCell(input_size, hidden_size)
self.fc2 = nn.Linear(args.rnn_hidden_dim, args.n_actions)
def forward(self, obs, hidden_state):
x = F.relu(self.fc1(obs))
h_in = hidden_state.reshape(-1, self.args.rnn_hidden_dim)
h = self.rnn(x, h_in) # GRUCell 的输入要求(current_input, last_hidden_state)
q = self.fc2(h) # h 是这一时刻的隐状态,用于输到下一时刻的RNN网络中去,q 是真实行为Q值输出
return q, h
2.4 Critic 网络设计
在 2.1 中我们提出了独立行为回报
D
a
D^a
D
a
的计算方法,计算公式为:
D
a
=
r
(
s
,
u
)
−
r
(
s
,
(
u
−
a
,
c
a
)
)
D^a = r(s, \textbf{u}) – r(s, (\textbf{u}^{-a}, c_a))
D
a
=
r
(
s
,
u
)
−
r
(
s
,
(
u
−
a
,
c
a
)
)
但是,如果按公式,如果想计算出所有动作的
D
a
D^a
D
a
值,就需要将每个动作都替换成默认行为
c
a
c_a
c
a
去与环境互动一次得到最终结果,这样采样次数会非常多。此外,到底选择哪一个行为当作默认行为才是最合适的呢?很难决定。
为此,COMA 就提出了使用 Critic 网络来计算
D
a
D^a
D
a
。既然我们无法决定哪一个行为作为 “默认行为” 是最好的,那我们就干脆取所有行为的 “平均效用值” 作为 “默认行为” 的行为效用值吧,这样就不用纠结选择哪一个行为最合适了,并且 “均值” 本身听起来就很符合 baseline 的概念嘛。
注意:我在这里的 “平均效用” 上打了引号,准确来说应该是所有行为效用的 “期望”,即 行为效用 * 行为概率,而非简单的求平均。
这样一来,默认行为行为效用计算公式就变成了:
Q
(
s
,
c
a
)
=
∑
u
a
′
π
a
(
u
′
a
∣
τ
a
)
Q
(
s
,
(
u
−
a
,
u
′
a
)
)
Q(s, c_a) = \sum_{u_a’}\pi^a(u’^a|\tau^a)Q(s, (\textbf{u}^{-a}, u’^a))
Q
(
s
,
c
a
)
=
u
a
′
∑
π
a
(
u
′
a
∣
τ
a
)
Q
(
s
,
(
u
−
a
,
u
′
a
)
)
那么我们就可以将
D
a
D^a
D
a
等效近似于
R
(
s
,
u
)
R(s, \textbf{u})
R
(
s
,
u
)
啦:
R
a
(
s
,
u
)
=
Q
(
s
,
u
)
−
∑
u
a
′
π
a
(
u
′
a
∣
τ
a
)
Q
(
s
,
(
u
−
a
,
u
′
a
)
)
R^a(s, \textbf{u}) = Q(s, \textbf{u}) – \sum_{u_a’}\pi^a(u’^a|\tau^a)Q(s, (\textbf{u}^{-a}, u’^a))
R
a
(
s
,
u
)
=
Q
(
s
,
u
)
−
u
a
′
∑
π
a
(
u
′
a
∣
τ
a
)
Q
(
s
,
(
u
−
a
,
u
′
a
)
)
说了这么多,好像根本没有跟中心 Critic 扯上啥关系咧?别急,现在就有关系了。
还记得我们要计算
Q
(
s
,
c
a
)
Q(s, c_a)
Q
(
s
,
c
a
)
吧?我们需要把一个 Agent 所有的行为的 Q 值拿出来乘以对应行为的选择概率才是最后的结果。行为概率简单,我们 Actor 网络最后的输出值走一遍 softmax 层就好了,但是行为的 Q 值怎么得到呢?
这时候就需要 Critic 出场了。
COMA 中的 Critic 网络接收 5 个输入:当前全局状态,当前 agent 的观测,除自身外其他 agent 的联合行为,自身 agent 的 one-hot 编码,所有 agent 上一时刻的行为。
输出:当前 agent 所有可执行行为的 Q 值。
具体对应这张图:
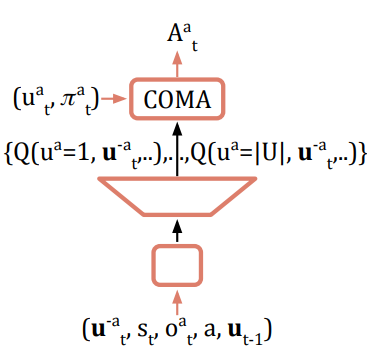
这样一来,我们每个 agent 对应的所有行为的 Q 值就能拿到了,再乘上 softmax 输出的行为概率,就得到
Q
(
s
,
c
a
)
Q(s, c_a)
Q
(
s
,
c
a
)
啦。
Critic 网络代码如下:
class ComaCritic(nn.Module):
def __init__(self, input_shape, arglist):
"""
输入:当前的状态、当前agent的obs、其他agent执行的动作、当前agent的编号对应的one-hot向量、所有agent上一个timestep执行的动作
输出:当前agent的所有可执行动作对应的联合Q值,一个n_actions维向量
"""
super(ComaCritic, self).__init__()
self.arglist = arglist
self.fc1 = nn.Linear(input_shape, arglist.critic_dim)
self.fc2 = nn.Linear(arglist.critic_dim, arglist.critic_dim)
self.fc3 = nn.Linear(arglist.critic_dim, self.arglist.n_actions)
def forward(self, inputs):
x = F.relu(self.fc1(inputs))
x = F.relu(self.fc2(x))
q = self.fc3(x)
return q
2.5 训练流程(Update Parameters)
COMA 一共存在 2 个网络,Actor 和 Critic,因此整个模型训练中也包括了对应的 2 个模型更新过程。
我们先来看 COMA 更新函数的代码:
def learn(self, batch, max_episode_len, train_step, epsilon):
...
# 计算每个 agent 的 Q 值更新 Critic
q_values = self._train_critic(batch, max_episode_len, train_step) # 训练critic网络,并且得到每个agent的所有动作的Q值
action_prob = self._get_action_prob(batch, max_episode_len, epsilon) # 走一遍softmax得到每个agent的所有动作的概率
q_taken = torch.gather(q_values, dim=3, index=u).squeeze(3) # 每个agent的选择的动作对应的Q值
pi_taken = torch.gather(action_prob, dim=3, index=u).squeeze(3) # 每个agent的选择的动作对应的概率
log_pi_taken = torch.log(pi_taken)
# 计算 baseline 和 R(s, u) 更新 actor
baseline = (q_values * action_prob).sum(dim=3, keepdim=True).squeeze(3).detach()
advantage = (q_taken - baseline).detach()
loss = - (advantage * log_pi_taken).sum()
self.rnn_optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(self.rnn_parameters, self.arglist.grad_norm_clip)
self.rnn_optimizer.step()
...
从上述代码可以看出,整个 learn 函数包含了两次 backward(),一次是 critic 网络的反向更新,一次是 actor 网络的反向更新。下面我们对这两个网络的更新分别做讲解。
Critic 网络更新
Critic 网络的更新同样使用 TD-Error 的方式进行更新,只是采用的是 TD(
λ
\lambda
λ
) 的形式,Loss 函数如下:
L
o
s
s
=
(
y
(
λ
)
−
f
θ
c
(
⋅
)
)
2
Loss = (y^{(\lambda)} – f^{\theta^c}(·)) ^ 2
L
o
s
s
=
(
y
(
λ
)
−
f
θ
c
(
⋅
)
)
2
其中:
y
(
λ
)
=
(
1
−
λ
)
∑
n
=
1
∞
λ
n
−
1
G
t
(
n
)
G
t
(
n
)
=
∑
l
=
1
n
γ
l
−
1
r
t
+
l
+
γ
n
f
θ
c
(
⋅
)
y^{(\lambda)} = (1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}G_t^{(n)} \\ G_t^{(n)} = \sum_{l=1}^n\gamma^{l-1}r_{t+l} + \gamma^nf^{\theta^c}(·)
y
(
λ
)
=
(
1
−
λ
)
n
=
1
∑
∞
λ
n
−
1
G
t
(
n
)
G
t
(
n
)
=
l
=
1
∑
n
γ
l
−
1
r
t
+
l
+
γ
n
f
θ
c
(
⋅
)
也就是说,Loss 函数公式可以表示为:
L
o
s
s
=
(
(
1
−
λ
)
∑
n
=
1
∞
λ
n
−
1
(
∑
l
=
1
n
γ
l
−
1
r
t
+
l
+
γ
n
f
(
⋅
)
)
−
f
(
⋅
)
)
2
Loss = ((1-\lambda)\sum_{n=1}^\infty \lambda^{n-1}(\sum_{l=1}^n\gamma^{l-1}r_{t+l} + \gamma^n {\color{red}f(·)}) – f(·)) ^ 2
L
o
s
s
=
(
(
1
−
λ
)
n
=
1
∑
∞
λ
n
−
1
(
l
=
1
∑
n
γ
l
−
1
r
t
+
l
+
γ
n
f
(
⋅
)
)
−
f
(
⋅
)
)
2
其中,红色部分的 f() 是使用 target critic network 预测的值,后一个 f() 是使用 evaluate critic network 预测的值。
整个 Critic 更新代码如下所示:
def _train_critic(self, batch, max_episode_len, train_step):
...
# 得到每个 agent 对应的Q值,维度为 (episode个数, max_episode_len, n_agents,n_actions)
# q_next_target为下一个状态-动作对应的 target 网络输出的Q值,没有包括reward
q_evals, q_next_target = self._get_q_values(batch, max_episode_len)
q_values = q_evals.clone() # 在函数的最后返回,用来计算advantage从而更新actor
# 取每个agent动作对应的Q值,并且把最后不需要的一维去掉,因为最后一维只有一个值了
q_evals = torch.gather(q_evals, dim=3, index=u).squeeze(3)
q_next_target = torch.gather(q_next_target, dim=3, index=u_next).squeeze(3)
targets = td_lambda_target(batch, max_episode_len, q_next_target.cpu(), self.arglist)
td_error = targets.detach() - q_evals
loss = (masked_td_error ** 2).sum() / mask.sum()
self.critic_optimizer.zero_grad()
loss.backward()
return q_values
Actor 网络更新
由于 COMA 是基于 Policy-Based 的方法,为此 Actor 更新使用传统的 PB 更新公式:
g
=
▽
θ
π
l
o
g
π
(
u
∣
τ
t
a
)
A
(
s
,
u
)
g = \bigtriangledown_{\theta_\pi}log\pi(u|\tau_t^a)A(s, u)
g
=
▽
θ
π
l
o
g
π
(
u
∣
τ
t
a
)
A
(
s
,
u
)
其中,这里的
A
(
s
,
u
)
A(s, u)
A
(
s
,
u
)
使用 COMA 提出的独立回报计算获得,使用
D
a
D^a
D
a
即
R
(
s
,
u
)
R(s, u)
R
(
s
,
u
)
来进行等效代替。
此时,梯度(Loss)的计算公式变成如下所示:
g
=
▽
θ
π
l
o
g
π
(
u
∣
τ
t
a
)
(
Q
(
s
,
u
)
−
∑
u
a
′
π
a
(
u
′
a
∣
τ
a
)
Q
(
s
,
(
u
−
a
,
u
′
a
)
)
)
g = \bigtriangledown_{\theta_\pi}log\pi(u|\tau_t^a)(Q(s, \textbf{u}) – \sum_{u_a’}\pi^a(u’^a|\tau^a)Q(s, (\textbf{u}^{-a}, u’^a)))
g
=
▽
θ
π
l
o
g
π
(
u
∣
τ
t
a
)
(
Q
(
s
,
u
)
−
u
a
′
∑
π
a
(
u
′
a
∣
τ
a
)
Q
(
s
,
(
u
−
a
,
u
′
a
)
)
)
actor 更新代码如下:
# 计算 baseline 和 R(s, u) 更新 actor
baseline = (q_values * action_prob).sum().detach()
advantage = (q_taken - baseline).detach()
loss = - (advantage * log_pi_taken).sum()
self.rnn_optimizer.zero_grad()
loss.backward()
3. COMA 效果
实验结果如下图所示,其中3m,5m分别指代一个作战小队中包含3个,5个marine(一种兵种);2d_3z指代一个作战小队中包含2条龙和3个狂热者。
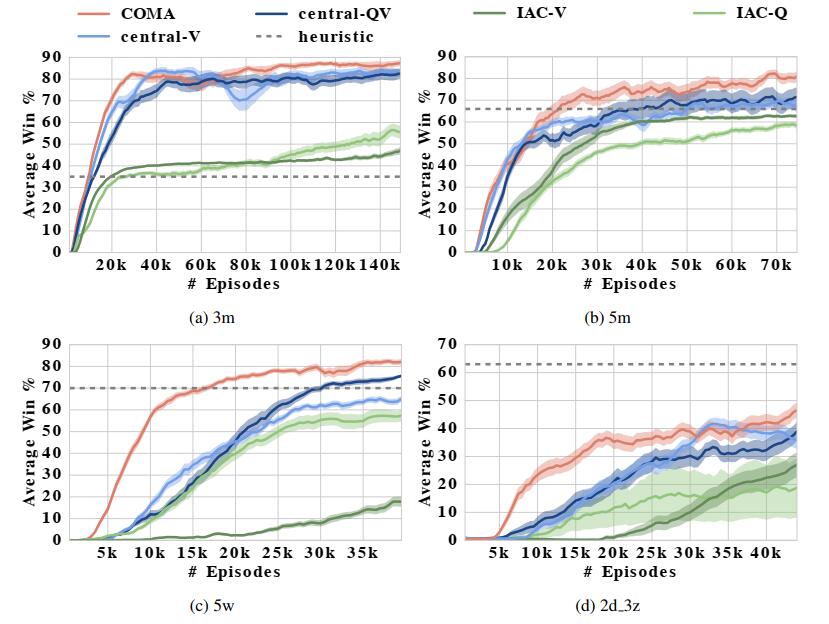
COMA 论文链接:https://arxiv.org/pdf/1705.08926.pdf
COMA 实现代码:https://github.com/oxwhirl/smac