博客

本篇博客是我选择这篇文章的一部分整理得，添加了一些我得理解和注释，方便我研究代码。原文**《Fast, Exact, Linear Booleans》**我上传了。

摘要

我们提出了一个新的系统，用于在线性3D多面体上可靠地执行布尔运算。我们的系统是精确的，这意味着所有内部数字谓词都是从精确的几何计算中确定的。我们的基于BSP树的系统执行迭代计算的速度比基于CGAL的Nef Polyhedra的系统快16-28倍，后者是鲁棒布尔运算的当前最佳实践，但速度却是非鲁棒建模器Maya的两倍。同时，与以前的工作相比，我们获得的几何子例程要小得多，它仅包含4个谓词，凸多边形构造函数和凸多边形分割例程。在此基础上使用基于BSP树的布尔算法使我们能够显式处理所有几何退化（曲面变成平面，线变成了点），而无需面对大量复杂情况。

1介绍

尽管存在悠久的鲁棒性问题，但布尔集操作（又名构造实体几何或CSG）仍然是大多数可用3D建模系统中的流行选择。该操作非常符合建筑物体中正负空间的建筑概念，比如：CAD / CAM中的机械零件加工以及从形状中添加和移除虚拟材料的通用“雕刻”操作。我们构建了此处描述的系统来解决此类雕刻应用程序，对于这些应用程序，我们发现现有的布尔运算缺乏速度和鲁棒性，尤其是在执行迭代运算时，例如用工具重复刨削对象。雕刻是一个特别具有挑战性的应用程序，因为即使是差强人意的产品也需要快速（实时）和完全健壮（零故障）的解决方案才能使用，这与计算机图形社区中许多人的期望相反。我们发现，可以使多面体上的布尔运算足够快和强大，以使其成为此类应用程序的可行组件。

研究鲁棒几何的第一个也是最大的动机之一是，由于尝试执行布尔运算而看到系统崩溃。尽管对该问题进行了20年的研究，但最新的健壮布尔运算[HK05]的运行速度可能比非健壮运算慢20倍。在我们的实验（第4节）中，这些性能表征表现得更好。我们看到的情况是，最新技术（CGAL）所花费的时间是非鲁棒布尔值的50倍以上。当我们与在娱乐和建筑设计建模者中实现布尔运算的从业人员交谈时，没有人知道对几何鲁棒性的任何研究。他们认为，除了使用Matlab / Mathematica风格的大数计算外，没有其他解决方案来解决其鲁棒性问题，他们认为这过于昂贵。鉴于上述Hachenberger等。过去的20年中，论文[HK05]构成了唯一一项超过一次测试的实验，很容易看出这种印象是如何持续的。


贡献


我们展示了一个系统，它能够计算出完全鲁棒的（即精确的）线性布尔运算，其运算速度仅是非鲁棒的（即易碎的）建模器Maya的两倍，从而提供了第一个经验证据，证明了几何鲁棒性技术实际上是可行的。计算布尔运算。据我们所知，这是有史以来进行和发布的非健壮的商业布尔和健壮的布尔系统之间的第二次也是最大的比较测试。我们使用新颖的技术来完成此任务，该技术的使用时间大多为15-20年。除了对这些技术进行一些小的但重要的更改外，我们还提出了一种新的基于平面的凸多边形分割算法（第3.2节）。

图1

：使用约9000个十二面体，依次减去基材将方块雕刻成一只兔子。我们的系统以大约1Hz的速率在大约3小时内计算了这些减法。使用较小实验的推断，CGAL得此计算将花费至少3天。 Maya甚至无法执行此计算，在前几百次操作中崩溃了。

我们描述了用于在基于点的多边形网格和基于平面的二进制空间分区树之间进行转换的输入/输出方法（第3.4节），但是I / O并不是我们的重点。我们不对转换的准确性（例如拓扑保留）做出任何有力保证，但可以在机器epsilon内准确执行转换算法。此外，当前系统对于基于平面的输入和基于点的输入都具有强大的性能（无崩溃/故障），此外，还确保了已经由平面表示的输入的100％准确的结果，例如使用原始多面体雕刻时（我们的原始动机）。

2.背景

2.1 稳健性

在Yap [Yap04]之后，“非稳健性是指几何算法中由于数值错误而导致的定性或灾难性故障。”也就是说，几何鲁棒性与精确数字不同。只要结果不是很不准确，就其本身而言，数字精度通常是无关紧要的。但是，小的数字错误有时会导致灾难性的程序故障（不一致）或严重错误的结果。几何鲁棒性旨在避免这些数值误差的副产品，而不会产生完全精确的数值的成本。

因此，几何鲁棒性一直并且一直是关于同时速度和鲁棒性。在没有另一个目标的情况下，任何一个目标都很容易实现。

几何程序中的数值计算可以分为谓词或构造[She06]。谓词根据几何对象的数字坐标做出两方向或三方向的决策，而构造则根据现有几何对象的已知坐标来计算新几何对象的坐标。通常，仅将自己限制在谓词上的算法比使用构造的算法更容易实现鲁棒和快速。通过限制谓词，每个谓词都基于几个数字进行决策，任何算术表达式的深度都具有先验常数界限。此界限允许使用静态过滤器[She97，FVW96]生成精确的快速谓词，这意味着它们始终提供正确的分支答案。相比之下，使用构造的算法允许构造任意深度的算术表达式，从而招致重大的速度损失，以确保得到准确的答案。在这项工作中，我们利用Sugihara和Iri的观察[SI89]，如果表示形式是基于平面而不是点，则线性布尔值不需要构造。

我们的解决方案之所以精确，是因为在输入一致的情况下，它是无条件健壮的。这也是一种固定精度的技术，因为我们可以通过使用基于平面的表示来避免构造，从而为所使用的任何算术树的深度以及所需的表示复杂度提供先验常数界限。这与没有这种限制的任意精度技术形成对比，这通常是因为它们使用结构[BMP93，GHH * 03]。正如我们将证明的（第4节），固定精度技术比任意精度技术要快得多。 Devillers和Pion [DP03]在其Delaunay三角剖分实验中提供了确凿的证据。

有许多非精确方法提供了较弱的健壮性概念。众所周知的示例包括epsilon-tweaking [NA T90，LTH86]，其中对启发式公差参数进行了调整，希望能够成功执行。用于CAD / CAM和实体建模的工业系统通常将这种技术与撤消操作一起使用，以允许用户解决失败的操作，但是它是脆弱的系统，因为它无法提供防止操作失败的保证。间隔几何技术[Seg90，Bru91]更原则化，该技术表示在保证的间隔内具有局部公差的几何图元。它们具有一定的鲁棒性，因为它们为表示的不精确性提供了有保证的边界，但是这些间隔可以任意变宽，最终将所有几何图形折叠到很大的间隔内的某个点。与epsilon调整一样，如果用户愿意解决这些问题，则基于此方法的系统可能会非常有用。但是，为了避免用户变通，最好使用高效的精确系统（有时是必需的）。


一般位置和几何简并性


除了上述数​​值问题外，许多算法还依赖于“一般位置”假设，例如“通常，两个曲面（2d）相交于一定数量的曲线（1d）”。违反这些假设的几何的局部排列称为（几何）简并性或简并排列。解决几何简并性的一种方法是不做一般位置假设，我们这样做。但是，对于某些算法，此方法会导致退化案例的大规模笨拙爆炸。因此，几何形状通常被扰动到大致位置。天真地做（通过直接修改坐标）扰动会产生进一步的复杂性。因此，鲁棒的扰动[Sei94]是象征性的，进一步需要使用准确性。

2.2 bool运算

我们（以及Maya和行业）遵循Requicha的正则化集形式主义[Req77]（

译者按：正则集合运算保证集合运算的结果仍是一个正则形体,即丢弃悬边、悬面等

）。 CGAL遵循Nef形式化[Nef78]。文献中有许多处理布尔值的特定方法，但是由于我们必须与曲面建模器进行互操作，因此我们关注那些支持边界评估从而可以输出网格的方法。


B-rep算法

[HHK89，LTH86]是最常见的算法，它们与更新的单元格复杂算法[GHH * 03，HK05]共享算法模板。该模板为：1）如果A和B是我们要计算其并集，差值或交集的两个对象，请找到A和B的交集，从而将每个表面分为两个分量，一个在内部，一个在外部。 2）选择每个表面的适当组件，3）然后将它们缝合在一起以形成正确的输出。这种明显的简单性掩盖了由于两个对象可以通过各种方式对齐而导致的大量特殊情况[Hof89]。结果系统可能非常复杂，因此很难确定是否所有情况都已得到处理。可以通过使用扰动技术（第2.1节）[For97]来减少这种分析，但是我们还没有遇到任何明确提出B-rep算法完整几何理论的出版物。


CSG树

将对象编码为原始对象的布尔组合（例如（A∪（B∩C））-D）。在CSG树上计算布尔运算通常很简单，真正的问题是产生有问题得边界[RV85]。这可以通过简化为Brep算法或通过在树上全局操作并利用受限原语集的属性的算法来实现[Bru91，BR96]。但是，这些方法不适用于迭代的交互式应用程序。


BSP树

提供了B-rep算法的替代方法，通过明确处理所有退化的几何结构[TN87，NA T90]，避免了B-rep算法的伴随爆炸。这些已被证明对交互式体积雕刻具有合适的性能[Nay90]，而最近的工作[LDS09]则建议进一步改善性能。不幸的是，所有这些方法都是脆弱的，因此容易出现故障和用户变通办法。我们将在短期内详细介绍此方法（第3.3节）。

除了BSP树之外，最接近我们系统的是Fortune [For97]。像我们一样，《财富》杂志运用Sugihara和Iri在飞机上的观察结果以及固定精度技术来增强鲁棒性。除此之外，我们几乎没有共同之处。我们使用不同的谓词，完全不同的表示形式：BSP树而不是Breps，并且我们不依赖于符号扰动，而是选择显式地（并使用更简单的衬底）处理所有退化的排列。这些差异都是我们实现鲁棒性和性能相结合的关键设计决策的结果。


采样量

提供了另一种选择-网格离散化-通常提倡雕塑环境[GH91]。这种方法由Ferley，Cani和Gascuel [FCG00]进行了改进，并与Perry和Frisken的Kizamu [PF01]达到了顶峰，它们能够处理多达12层深的八叉树。 Kizamu的两个主要缺点阻止了我们进一步采用体积方法：（a）随着接近12个八度的八叉树，渲染变得过于昂贵，并且（b）离散化错误（对感知的视觉质量比舍入更有害）仍然存在。

3.系统设计

尽管我们一开始尝试基于Thibault和Naylor的BSP树算法[TN87，NA T90]构建一个布尔雕刻系统，但是反过来激发和解释我们的设计可能更容易；也就是说，自下而上。正如Sugihara和Iri指出的那样，为了使用固定精度技术（第2.1节），必须使用平面而不是点作为基本原语（

原语是指基本单元，图形学里指基本图元，比如点，线，面等

）。我们从这个决定开始。自然地，我们的数字谓词都必须被表述为关于平面的谓词（

谓词是数理逻辑中表示一个个体的性质和两个或两个以上个体间关系的词。

）。同样，几何定义和子例程现在必须从这些谓词中引导出来，并因此在平面操作方面完全用原语表达。最后，使用二进制空间分区是因为它们是（a）基于平面的，并且（b）允许考虑几何底物得经济性。

3.1 数值底物

在我们的系统中，平面被视为四元的浮点数（a，b，c，d），它们被解释为平面方程的系数。有时，我们有理由提及“点”，这并不是指三元坐标。相反，我们将一个点设为三平面（p，q，r），它们的相互交点是我们关注的点。我们不使用或引用线。我们提供了关于平面及其在空间中的相对位置的四个算术谓词[YN97，Sto87]。


一致性

当且仅当以下矩阵的所有2×2个的行列式为零时，两个平面p，q才是重合的：




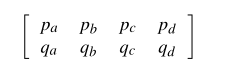
重合方向

此外，如果已知pandqq是重合的，则当且仅当所有乘积paqa，pbqb，pcqc，pdqdd均为非负数时，p的方向才类似于q。


点效度

当且仅当以下行列式为非零时，点（p，q，r）定义良好（即有效）：




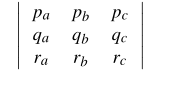
方向

给定点（p，q，r）有效，则当且仅当以下表达式分别为负，零或正时，它位于平面s的后面，上方或前面：



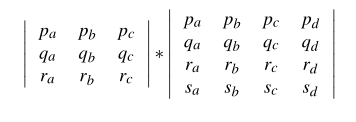
这些谓词以Shewchuk [She97]的形式实现为静态过滤的浮点谓词。我们与Shewchuk的模式有些偏差。首先，我们的谓词仅采用单精度浮点输入，但是使用双精度进行性能计算，这使我们能够保证不存在指数上溢/下溢，并允许我们加强静态误差范围。其次，我们不使用辅助因子展开，而是将4×4行列式计算为Plücker坐标形式的两条线之间的点积。这使算术树变浅，从而再次导致更严格的静态错误范围。最后，为简单起见，我们仅使用单级滤波器。

3.2.几何基材

在数字基板的上一部分中，我们将平面定义为基本体，将点定义为平面的三元组，并在这些平面上操作了4个谓词。现在，我们将定义凸多边形类型以及构造函数和拆分例程。这两个子例程构成整个几何对象。它们用于支持子超平面构造，树拆分和输入/输出转换（第3.3节，第3.4节）。


凸多边形

我们将一个凸多边形（在本文中，“多边形”始终代表“凸多边形”）作为支撑平面s，并以逆时针顺序列出一系列边界平面{bi}i∈Zn。然后，该多边形的顶点由vi =（s，bi-1，bi）给出。


从平面构造凸多边形

给定一个平面h，此操作将构造一个表示h的凸多边形，并用“很大的盒子”剪裁。这样，输出多边形可作为无限范围平面的替代。一致的轴对齐“非常大的框”用于对构造函数的所有调用，并且由平面x +，x-，y +，y-，z +，z-界定的空间量组成。

为了形成最终的多边形，找到了h法线的主要成分。不失一般性，将其设为hz。然后，以h为支撑，以x +，x-，y +，y-为边界组合形成多边形P。边界的顺序可以通过检查hz的符号来确定。最后，使用（下面的）多边形拆分程序对P进行z +和z裁剪，以确保整个多边形位于“很大的盒子”内。


通过平面拆分凸多边形

由于多边形拆分可以看作是多边形裁剪的两个连续且互补的实例，因此为简单起见，我们将介绍一种多边形裁剪算法。给定一个凸多边形（s，{bi}i∈Zn）和裁剪平面h，我们希望输出该多边形位于h的正侧的部分，或表示不存在这样的部分。

我们的算法类似于Sutherland-Hodgman风格的多边形快剪，在该步骤中，每个步骤都决定“执行或不输出当前顶点”，但我们决定“执行或不输出当前边界平面（边）”。类似地，我们决定是否以及何时将分割平面插入输出流中，而不是决定是否以及何时将交叉点插入输出流中。这些更改是消除线平面相交结构的关键，说明了“使用平面而不是点”的原理。

If s is coincident with h
If s is similarly oriented to h
Return (s,{bi}i∈Zn)
Else
Return nothing
Else
For i ∈ Zn(in order),
Output planes as specified by table lookup using:
o(s,bi−2,bi−1,h)
o(s,bi−1,bi,h)
o(s,bi,bi+1,h)
Return (s,output)
Algorithm: Clip (s,{bi}i∈Zn) by h

该算法通过迭代多边形的边界平面并确定是否输出每个边界平面bi来进行。为了做出此决定，针对裁剪平面h测试了bi，vi =（s，bi-1，bi）和vi + 1 =（s，bi，bi + 1）的两个端点。此外，还测试了紧邻的顶点vi-1 =（s，bi-2，bi-1）。随着我们的进行，测试这个额外的第三个顶点的原因将显而易见。





图2

：（左）编码示例（中和右）这两种情况仅使用两个顶点是无法区分的。


假定每个顶点可能位于剪切平面h的（-）之后，（0）或前面（+），则顶点vi-1，vi，vi + 1的每个三元组可能位于相对的27种可能排列之一中到修剪平面h。作为简写，我们使用以下编码方案。假设vi-1位于（0）h，位于（-）h之后，并且vi + 1位于h的前面（+）。然后使用序列0- +编码此排列。 （图2）

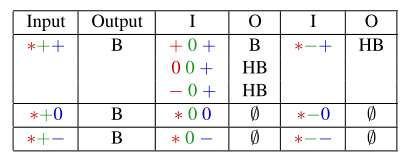
对于这27个代码中的每一个，我们必须决定是否输出当前的边界平面bi（信号B）（不输出信号）。我们必须决定是否输出剪切平面h（信号H）（不输出信号）；如果要同时输出两者，则必须确定输出的相对顺序（BH或HB）。为了完成该过程，将输出平面（如果有的话）按顺序用作生成的修剪多边形的边界平面列表。

在获得正确的输出时，应注意以下两个陷阱。必须确保不给H信号一次以上，并且在bi的对应边（vito vi + 1）位于剪切平面h中的情况下，切勿输出边界平面bi和剪切平面h。我们通过选择仅在重新输入正半空间时才输出h来解决前一个陷阱。我们通过忽略问题bi中边界平面的输出，并在多边形转回正半空间时输出裁剪平面h来解决后一个陷阱。


表1

：多边形裁剪编码（*是通配符）

在这里插入图片描述

3.3. BSP树集操作

Thibault，Amanatides和Naylor [TN87，NA T90]提出了使用BSP树对多面体进行布尔集运算的算法。与基于Brep的方法相比，该方法具有以更简单和更统一的方式处理简并性的优点，但是它容易出现数值鲁棒性问题。我们使用完全基于平面的此方法的修改，以便允许使用我们高效，坚固的基板。我们提供了BSP树方法的高级概述，然后描述了与Thibault和Naylor [TN87]和Naylor等人中详细描述的算法的偏差。 [NA T90]。





图3

：代表蓝色对象的BSP树






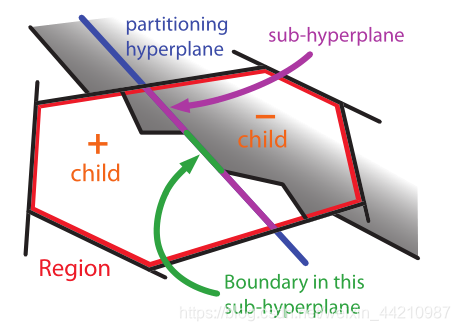
图4

：BSP树内部节点的部分（单元图）


BSP树如何表示对象？使用平面，BSP树将空间递归地划分为（凸的，可能是无边界的）单元。 BSP树的叶子对应于分区中不可分割的单元。通过简单地用两个标签（IN或OUT）之一为每个叶细胞着色，我们得到了由所有IN着色细胞组成的多面体集的表示。 （图3）BSP树的内部节点代表分区的可分割单元。每个这样的细胞有一个关联的“区域”，它是从根到此节点的路径上下降的一组半空间。这些半空间的交点，在几何上定义了该区域，即单元的范围。在树的节点上存储了分区（超）平面，该分区（超平面）与该区域一起可以找到子超平面，即超平面的一部分位于节点的区域中。此外，维护正负子指针。 （图4）

BSP树如何表示对象的边界？边界存储在BSP树的内部节点上，作为树的扩充。 BSP树的每个内部节点都存储在其关联的子超平面内的边界部分，表示为一组凸多边形。对我们来说，这些是基于平面的多边形。对于Thibault和Naylor，它们是基于点的多边形。





图5

：联合操作的结果


您如何计算BSP树之间的集合运算（例如A∪B）？将两个操作数（二进制空间）分区“合并”到新的（二进制空间）分区中（图5）。通过将一棵树与另一棵树的根分区重复拆分，可以找到此新分区，从而将设置操作问题减少到每一步的两个较小实例。在每个操作数对象A和B中，此最终分区的叶单元为IN或OUT。因此，如果所得叶为IN A或B，则将其着色为IN；如果将A和B均为OUT，则将其着色为OUT（并且类似地）具有相交和差异的不同逻辑）。





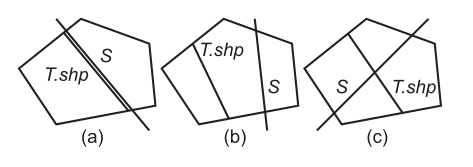
图6

：（a）T.shp和S∩T.区域是重合的，并且方向相似或相反。 （b）T.shp和S∩T.区域不相交，并且以四个可能组合之一相对定向。 （c）T.shp和S∩T。区域相交。


退化如何处理？ （即，如何拆分树？）给定一个子树T位于一个区域中（图4），然后用一个平面用S对其进行拆分，我们先拆分T的子超平面（T.shp），然后递归拆分T的子树。为此，我们只需确定T.shp和S∩T.region相对于彼此的位置。图6显示了出现的7种可能的布置。确定这7个参数中的哪个是简单的事情，只需将S.Thp分为S，将S.T.region分为T.hp。

您如何计算这个新的合成对象A∪B的边界？新边界必须由两个旧边界的某些子集组成。因此，我们可以使用新树对旧边界进行分类，以查看应该保留哪些面。

我们可以在BSP树及其子树上递归地实现大多数这些操作。此外，通过将新边界和BSP树的计算交织在一起，我们可以非常高效。通过使用在计算中获得的信息，我们可以避免不必要的工作，例如递归算法可以快速确定A的整个子树与B不相交，因此存储在该子树中的边界不会被set操作修改。这样，BSP树通过将其等同于树结构的结构局部性而自然地利用了空间局部性。

3.4.互操作性：输入和输出

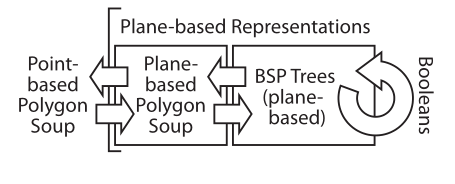
我们描述的系统旨在在经过净化的对象世界中工作，这些对象表示为基于平面的BSP树。不幸的是，没有其他操作或系统旨在在这个世界上工作。为了适应这些情况，我们提供以下转换：在点和基于平面的多边形汤之间，然后在基于平面的多边形汤和BSP树之间。这样，可以将基于平面的BSP树表示的输入和输出分解为4个更简单的转换。


点→平面

。每个基于点的多边形由基于平面的多边形近似。首先，将平面拟合到基于点的多边形的顶点，以用作新的基于平面的多边形的支撑平面s。使用平面到多边形的构造（第3.2节），将创建一个初始多边形。然后，针对基于点的多边形的每个边缘，制作一个新的边界平面，该边界平面穿过该边缘并与支撑s的平面正交。然后，使用多边形拆分程序（第3.2节）将这些边界平面依次裁剪为初始多边形。


平面→BSP树

。因为我们不能保证所得的基于平面的多边形汤是水密的，所以我们假设最坏的情况并实施网格修复算法。 Murali和Funkhouser基于BSP树[MF97]设计了一个聪明的网格修复方案。网格修复方案会建立一个一致的BSP树作为中间步骤，因此非常适合此角色。或者，如果我们知道基于平面的多边形汤是水密的（例如，如果它是从BSP树中提取的边界），那么我们可以使用标准的BSP树构建算法，例如Thibault所描述的算法和Naylor [TN87]。

**BSP树→平面。**由于边界已经存储在BSP树中，因此我们要做的就是遍历树并收集它。作为次要说明，出于前面提到的原因（第3.3节），我们可能想在重新计算树的边界之前进行一次。


平面→点

。由于基于平面的多边形的顶点被隐式定义为3个给定平面的交点（第3.2节），我们可以通过计算/逼近这些顶点的坐标来转换为基于点的输出。

**连接性。**尽管我们从不使用或记录连接性信息（就像使用B-rep时那样），但许多其他程序希望找到在其输入多边形汤中编码的连接性信息。当两个不同的多边形的两个顶点实际上是空间中的同一点时，可以准确地知道所有这些信息。由于可以保证BSP树输出的任何基于平面的多边形汤都是有效的，因此我们可以使用方向谓词从平面汤中恢复该顶点关联信息。给定两个有效点（a，b，c）和（x，y，z）（定义为平面的三倍），则当且仅当（a ，b，c）位于三个平面x，y和z上。


准确性

。就我们的目的（雕刻）而言，准确性仅对（a）直至目视检查和（b）为了实现鲁棒性很重要。为此，我们在转换的准确性（给定转换步骤的输入和输出之间的一致性）与输出的有效性（表示的自洽性）之间进行区分。请注意，建议的I / O路径始终确保有效性。因此，程序不会崩溃或失败。但是，I / O步骤并不总是保证100％的准确性。特别是，基于点和平面的面之间的转换计算不精确，从而使其具有舍入误差。仅在这些转换中丢失数字精度。 （使用Shewchuk的谓词所基于的Priest的技术[Pri91]可以减轻在输入和输出侧加工epsilon的损失。）此外，输入过程中舍入引起的扰动会破坏每个非三面体顶点（度k> 3） ）变成k-2几乎重合，但截然不同的顶点，可能会引入微多边形和/或类似碎片的多边形。因为我们只关心外观检查的准确性，所以我们可以在输出中运行网格简化程序以折叠分割顶点并消除退化的多边形。由于这种网格简化仅依赖于有效的连接性数据才能稳健地运行，因此不会引入新的稳健性问题。