一、p阶k步差分定义说明
n阶差分
▽
x
t
\triangledown x_t
▽
x
t
为
x
t
x_t
x
t
的1阶差分:
▽
x
t
=
x
t
−
x
t
−
1
\triangledown x_t=x_t-x_{t-1}
▽
x
t
=
x
t
−
x
t
−
1
▽
2
x
t
\triangledown^2 x_t
▽
2
x
t
为
x
t
x_t
x
t
的2阶差分:
▽
x
t
=
▽
x
t
−
▽
x
t
−
1
\triangledown x_t=\triangledown x_t-\triangledown x_{t-1}
▽
x
t
=
▽
x
t
−
▽
x
t
−
1
▽
n
x
t
\triangledown^n x_t
▽
n
x
t
为
x
t
x_t
x
t
的n阶差分:
▽
x
t
=
▽
n
−
1
x
t
−
▽
n
−
1
x
t
−
1
\triangledown x_t=\triangledown^{n-1} x_t-\triangledown^{n-1} x_{t-1}
▽
x
t
=
▽
n
−
1
x
t
−
▽
n
−
1
x
t
−
1
k步差分
▽
k
x
t
\triangledown_k x_t
▽
k
x
t
为
x
t
x_t
x
t
的1阶差分:
▽
k
x
t
=
x
t
−
x
t
−
k
\triangledown_k x_t=x_t-x_{t-k}
▽
k
x
t
=
x
t
−
x
t
−
k
二、python实现
1. n阶差分
diff_p = diff(data, n=n) #默认k=1

2. k步差分
diff_k_step = data.diff(k)
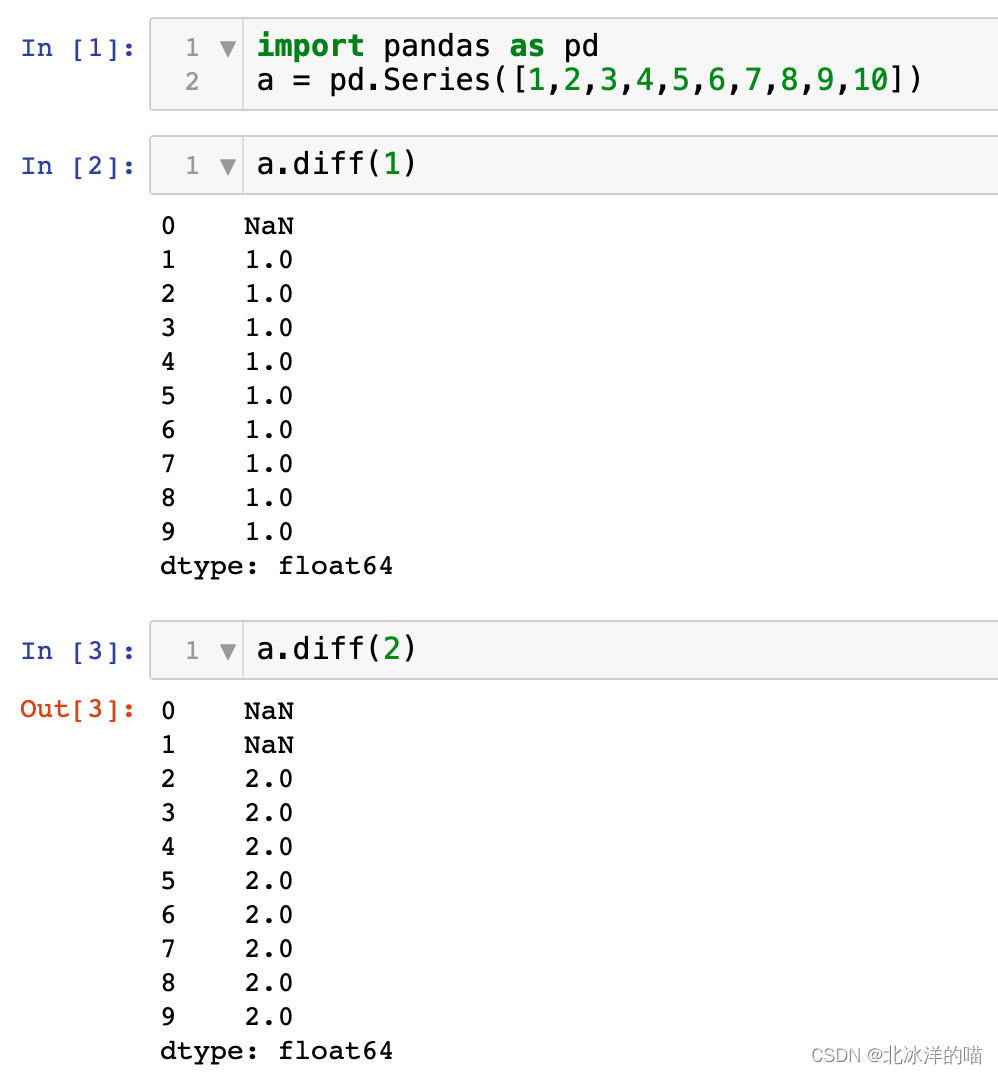
3. n阶k步差分
import numpy as np
# 定义一个长度为 10 的数组 x
x = pd.Series([1, 3, 6, 10, 15, 21, 28, 36, 45, 55])
n=2
k=3
for i in range(n):
x = x.diff(k)
y = x
print(y)