1 均值(Mean)、标准差(Standard deviation)、方差(Variance)
均值
X
‾
=
∑
i
=
1
n
X
i
n
\overline X=\frac{\sum_{i=1}^{n}X_i}{n}
X
=
n
∑
i
=
1
n
X
i
标准差
s
=
∑
i
=
1
n
(
X
i
−
X
‾
)
2
n
−
1
s=\sqrt{\frac{\sum_{i=1}^{n}(X_i-\overline X)^2}{n-1}}
s
=
n
−
1
∑
i
=
1
n
(
X
i
−
X
)
2
方差
s
=
∑
i
=
1
n
(
X
i
−
X
‾
)
2
n
−
1
s=\frac{\sum_{i=1}^{n}(X_i-\overline X)^2}{n-1}
s
=
n
−
1
∑
i
=
1
n
(
X
i
−
X
)
2
为什么要除以n-1,而不是n,但是翻阅资料,发现很多都是交代到,**如果除以n,对样本方差的估计不是无偏估计,比总体方差要小,要想是无偏估计就要调小分母,所以除以n-1。**那么问题来了,为什么不是除以n-2、n-3等等。所以在这里彻底总结一下,首先交代一下无偏估计。
2 无偏估计
以例子来说明,假如你想知道一所大学里学生的平均身高是多少,一个大学好几万人,全部统计有点不现实,但是你可以先随机挑选100个人,统计他们的身高,然后计算出他们的平均值,记为
X
‾
1
\overline X_1
X
1
。如果你只是
X
‾
1
\overline X_1
X
1
把作为整体的身高平均值,误差肯定很大,因为你再随机挑选出100个人,身高平均值很可能就跟刚才计算的不同,为了使得统计结果更加精确,你需要多抽取几次,然后分别计算出他们的平均值,分别记为
X
‾
1
,
X
‾
2
,
X
‾
3
,
.
.
.
X
‾
k
\overline X_1,\overline X_2,\overline X_3,…\overline X_k
X
1
,
X
2
,
X
3
,
.
.
.
X
k
:然后在把这些平均值,再做平均,记为:
E
(
X
‾
)
E(\overline X)
E
(
X
)
,这样的结果肯定比只计算一次更加精确,随着重复抽取的次数增多,这个期望值会越来越接近总体均值
μ
\mu
μ
,如果满足
E
(
X
‾
)
=
μ
E(\overline X)=\mu
E
(
X
)
=
μ
,这就是一个无偏估计,其中统计的样本均值也是一个随机变量,
X
‾
i
\overline X_i
X
i
就是
X
‾
\overline X
X
的一个取值。
无偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。
3 样本方差为何除以n-1?
介绍无偏估计的意义就是,我们计算的样本方差,希望它是总体方差的一个无偏估计,那么假如我们的样本方差是如下形式:
S
2
=
1
n
∑
i
=
1
n
(
x
i
−
X
‾
)
2
S^2=\frac{1}{n}\sum_{i=1}^n(x_i-\overline X)^2
S
2
=
n
1
i
=
1
∑
n
(
x
i
−
X
)
2
那么,我们根据无偏估计的定义可得:


由上式可以看出如果除以n,那么样本方差比总体方差的值偏小,那么该怎么修正,使得样本方差式总体方差的无偏估计呢?我们接着上式继续化简:
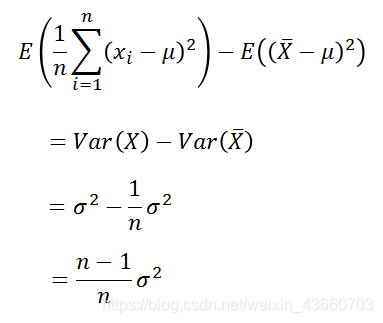
到这里得到如下式子,看到了什么?该怎修正似乎有点眉目。

如果让我们假设的样本方差
S
2
S^2
S
2
乘以
n
n
−
1
\frac{n}{n-1}
n
−
1
n
,即修正成如下形式,是不是可以得到样本方差是总体方差
σ
2
\sigma^2
σ
2
的无偏估计呢?

则:
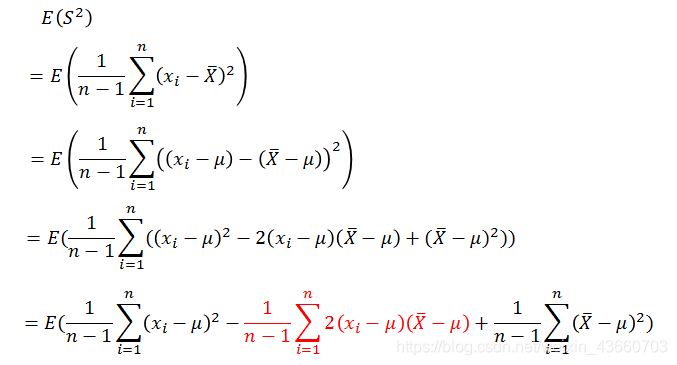
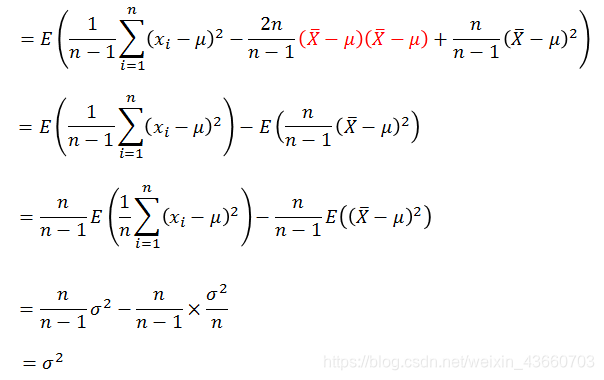
因此修正之后的样本方差的期望是总体方差
σ
2
\sigma^2
σ
2
的一个无偏估计,这就是为什么分母为何要除以n-1。
感谢大佬的指点:
参考文献