在开发中过程中,经常会遇到比较两个浮点数大小的问题。 根据业务需求,可能会有如下比较方式:
float a = 0.2323f;
float b = 0.2324343f;
if (a - b < 1e-2) {
// 若 a b之差在一个很小范围内,则可认为二者相等。
}
为什么要这么比较呢?因为一个计算机的“常识” ,即浮点数的表示不是精确的,而是近似的。
如下代码,将100个0.1相加,得到的结果并不刚好是10,而是 10.000002。
fun main() {
var sum = 0.0f
for (i in 1 .. 100) {
sum += 0.1f
}
println("sum is $sum")
}
// 这是一段用kotlin写的演示代码,运行结果如下:
sum is 10.000002
那么,浮点数为什么不能精确的表示呢?
首先,我们从十进制入手,将0.111111各位位权展开如下
| 0 | . | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|
| 0 * 10^0 | . | 1 * 10^-1 | 1 * 10^-2 | 1 * 10^-3 | 1 * 10^-4 | 1 * 10^-5 | 1 * 10^-6 |
可以看到,小数即对应位权指数为负数。拓展到二进制,也可如此表示,以两位小数为例。
| 0 | . | 0 | 1 | |
|---|---|---|---|---|
| 0 * 2^0 | . | 0 * 2^-1 | 1 * 2^-2 | 对应十进制:0.25 |
| 0 | . | 1 | 0 | |
| 0 * 2^0 | . | 1* 2^-1 | 0 * 2^-2 | 对应十进制:0.5 |
| 0 | . | 1 | 1 | |
| 0 * 2^0 | . | 1* 2^-1 | 1* 2^-2 | 对应十进制:0.75 |
可以看到,在二进制中连续的三个小数,0.01,0.10,0.11 转化成对应的十进制数后并不是连续的,中间差了很多。 如0.25到0.5,中间少了0.26,0.27,0.28 … 0.49 。
如果我们将小数在扩大两位,看看4位小数的二进制表示的范围有多大。
| 个位 | 小数点 | 第一位 | 第二位 | 第三位 | 第四位 | 对应十进制值 |
|---|---|---|---|---|---|---|
| 0 | . | 0 | 0 | 0 | 1 | 0.0625 |
| 0 | . | 0 | 0 | 1 | 0 | 0.125 |
| 0 | . | 0 | 0 | 1 | 1 | 0.1875 |
| 0 | . | 0 | 1 | 0 | 0 | 0.25 |
| 0 | . | 0 | 1 | 0 | 1 | 0.3125 |
| 0 | . | 0 | 1 | 1 | 0 | 0.375 |
| 0 | . | 0 | 1 | 1 | 1 | 0.4375 |
| 0 | . | 1 | 0 | 0 | 0 | 0.5 |
| 0 | . | 1 | 0 | 0 | 1 | 0.5625 |
| 0 | . | 1 | 0 | 1 | 0 | 0.625 |
| 0 | . | 1 | 0 | 1 | 1 | 0.6875 |
| 0 | . | 1 | 1 | 0 | 0 | 0.75 |
| 0 | . | 1 | 1 | 0 | 1 | 0.8125 |
| 0 | . | 1 | 1 | 1 | 0 | 0.875 |
| 0 | . | 1 | 1 | 1 | 1 | 0.9375 |
我们仍然看到,即使扩大位数,用二进制表示的小数也不能完全表示连续的十进制数。当位数不断扩大时,也只能表示更多的十进制浮点数,但也还是无法精确的表示对应的十进制浮点数。
故二进制表示的浮点数无法精确的转化成对应的十进制数,这是浮点数无法精确计算的根本原因。
只能通过位数更长的二进制数来无限接近十进制表示的浮点数。
在计算机中,为了更好表示浮点数,避免了上面这种直接的表示方法。 而是
采取了使用符号、尾数、基数、指数四部分来表示小数的方法
。这四部分的说明如下:

这个结构类似科学计数法。 但是在计算机中还有一些额外的规定来实现浮点数的存储。
在java中,浮点数分为单精度浮点数和双精度浮点数,它们有什么区别的呢?单精度的存储位数位32位,而双精度存储位数为64位。如何用这些位来存储浮点数的四个部分呢?
如下图分别为32位和64位浮点数的存储格式


对于符号位很好理解,只需一位即可,0表示正数,1表示负数。 和补码规则中的表示正负是一样的。
尾数部分则规定,将小数点前面的数固定为1,同时仅保留小数位的数字。 具体的推算过程过下,摘自《程序是怎样跑起来的》

注意,这里移动并不考虑符号位,因为符号位是用单独的一位来存储。 最终得到的23位即为对应的浮点数的尾数部分。
对于指数部分,采用的是excess系统表示方法,具体参考
百度百科
。 如下摘取部分定义
Excess系统是计算机中可以同时存储正数和负数的一种方法。
以32位浮点数为例,8为指数可以表示的范围为0到255,但是为了表示负数,需要将其中的一半划归负数。最大值255(1111-1111)的一半为127(0111-1111,舍弃了小数部分,可以用二进制位移的算法来考虑,即为127)
然后用0到127的这部分表示-127到0的,用128到255表示1到128。此时就避免了使用补码来表示负数了。
具体的对应关系如下表
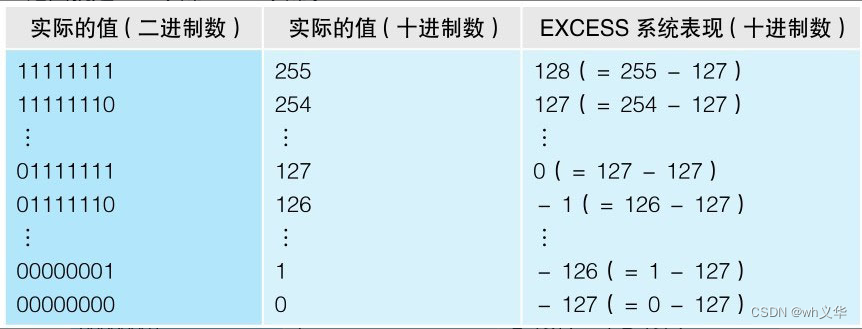
有了如上的规则,尝试使用规则将0.75换算为对应的二级制。
由于是正数,故符号位为0。
0.75用二进制表示为0.1100,为了将首位变为1,于是右移一位为1.100,然后将小数部分填充至23位,为10000000000000000000000。
由于尾数部分右移了一位,故指数应为-1。采用excess系统表示法,即为126,对应的二进制为 0111-1110.
综上,浮点数0.75在计算机中的表示为0-01111110-10000000000000000000000
采用书中的代码来校验一下,代码如下:
int main(void) {
float data;
unsigned long buff;
char s[34];
data = (float) 0.75;
memcpy(&buff, &data, 4);
for (int i = 33; i >= 0; i--) {
if (i == 1 || i == 10) {
s[i] = '-';
} else {
if (buff % 2 == 1) {
s[i] = '1';
} else {
s[i] = '0';
}
buff /= 2;
}
}
s[34] = '\0';
printf("%s\n", s);
return 0;
}
输出结果为:
0-01111110-10000000000000000000000
与推算的过程正好相符。 至此,就理解了浮点数在计算机中的存储方式。