昨晚睡觉前刷手机,看到一道傻子坐飞机的题目,是一道概率的题目.想了一下觉得还挺有意思的,写一个比较容易理解的解题方法.首先描述一下问题.
傻子坐飞机:假设有n个人(编号分别为从1,2,3…,n-1,n)要上飞机坐在n个座位上,飞机上的n个座位也有相应的编号1,2,3,…,n-1,n,假设每个人的座位选择规则为:
- 第一个人是个傻子,他上了飞机后会从n个座位中随机选择一个坐下.
- 除了第一个傻子以外,其余每个人上了飞机后,
2.1 如果他的座位没有被其他人占领,那么他一定要坐在自己的位置上.
2.2 如果他的座位已经被其他人占领了,那么他就在剩余没有被占领的座位上随机选择一个位置坐下.
那么在这样的选座位规则下,最后一个上飞机的人,他能坐在自己位置上的概率是p多少?
由于这n个人除了第一个傻子以外,其余的n-1个人是不同的且每个人都有一个相应的座位,所以他登机的顺序没有关系.那么不妨假设登机的顺序为第1号,第2号,…,第n号.我们记
p
(
n
)
p(n)
p(n)为总人数为n时的概率,为了便于理解,我们先来看简单的情况.
n=1时,显然这个人一定可以坐在自己的位置上,即
p
(
1
)
=
1
p(1)=1
p(1)=1.
n=2时,
- 如果第1个人坐在自己的位置上,那么最后一个人(也就是第2个人)也可以坐在自己的位置上;
- 如果第1个人没有坐在自己的位置(位置1)上,那么最后一个人也不能坐在自己的位置上(位置2)了.
即
p
(
2
)
=
1
2
∗
1
+
1
2
∗
0
=
1
2
p(2)=\frac{1}{2}*1+\frac{1}{2}*0=\frac{1}{2}
p(2)=21∗1+21∗0=21
n=3时,
- 如果第1个人坐在了自己的位置上,那么最后一个人也一定会坐在自己的位置上.
- 如果第1个人坐在了第2个位置上,那么剩余的2个人的座位选择相当于n=2时的情况.
- 如果第1个人坐在了第3个位置上,那么最后一个人肯定无法坐在自己的位置上.
即
p
(
2
)
=
1
3
∗
1
+
1
3
∗
p
(
2
)
+
1
3
∗
0
=
1
2
p(2)=\frac{1}{3}*1+\frac{1}{3}*p(2)+\frac{1}{3}*0=\frac{1}{2}
p(2)=31∗1+31∗p(2)+31∗0=21
相信大家已经看出了规律,很自然的推广到n个人的情况.一般的,对于n个人上飞机(n>=2),这个过程为:
- 如果第1个人坐在了自己的位置上,那么最后一个人也一定会坐在自己的位置上.对应的概率为
p
(
n
)
1
=
1
n
p(n)_1=\frac{1}{n}
p(n)1=n1
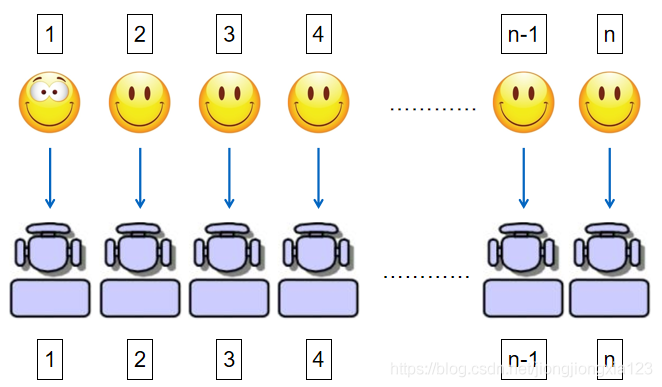
2.如果第1个人坐在了第2个位置上,那么可以将第1个人和第2个位置都删掉。
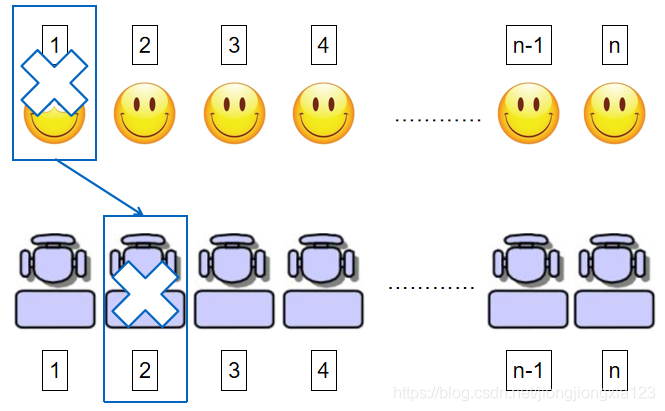
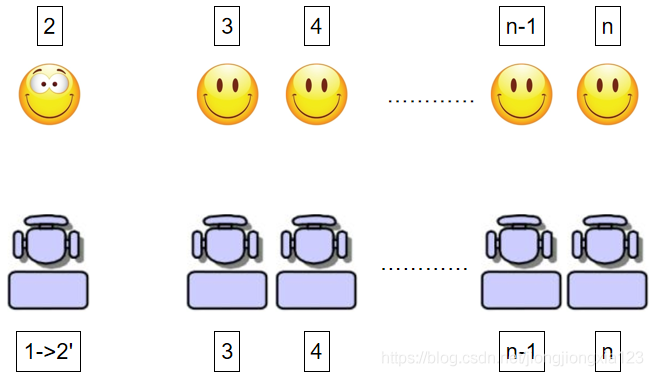
删除后,把第1个位置看做是第2个人对应的新位置,对于第2个人,由于他的座位被傻子占掉了,所以他只能从剩下的没有被占用的座位里随机选择一个,这种行为和问题定义中的傻子的行为是一样的,所以可以把第2个人看做是新的傻子.此时问题转换成了n-1个人上飞机的问题,对应的概率为p
(
n
)
2
=
1
n
∗
p
(
n
−
1
)
p(n)_2=\frac{1}{n}*p(n-1)
p(n)2=n1∗p(n−1)。
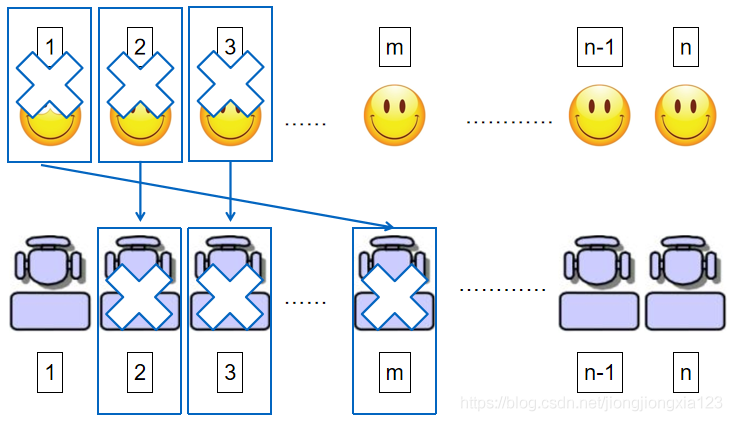
3.一般的,假设第1个人选到了第m个位置,对于第2、3、…、m-1个人,他们都可以去选择对应的第2、3、…、m-1的座位,所以这些人和相应的座位都可以被删掉。将第1个位置看做是第m个人对应的新位置,并将第m个人看做新的傻子,问题转化为m个人上飞机,对应的概率为
p
(
n
)
m
=
1
n
∗
p
(
m
)
p(n)_{m}=\frac{1}{n}*p(m)
p(n)m=n1∗p(m).
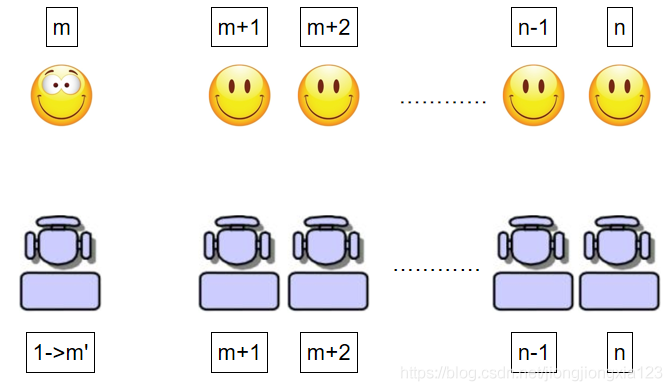
把所有情况归纳起来得到,
p
(
n
)
=
1
n
∗
1
+
1
n
∗
p
(
2
)
+
1
n
∗
p
(
3
)
+
.
.
.
+
1
n
∗
p
(
n
−
2
)
+
1
n
∗
p
(
n
−
1
)
=
1
n
(
p
(
1
)
+
p
(
2
)
+
.
.
.
+
p
(
n
−
1
)
)
p(n)=\frac{1}{n}*1+\frac{1}{n}*p(2)+\frac{1}{n}*p(3)+…+\frac{1}{n}*p(n-2)+\frac{1}{n}*p(n-1)=\frac{1}{n}(p(1)+p(2)+…+p(n-1))
p(n)=n1∗1+n1∗p(2)+n1∗p(3)+...+n1∗p(n−2)+n1∗p(n−1)=n1(p(1)+p(2)+...+p(n−1)).
即:
p
(
n
)
=
1
n
∑
i
=
1
n
−
1
p
(
i
)
p(n)=\frac{1}{n}\sum_{i=1}^{n-1}p(i)
p(n)=n1∑i=1n−1p(i)
我们得到了数列
p
(
n
)
p(n)
p(n)的递推公式,下面来计算一下
p
(
n
)
p(n)
p(n)的通项公式.稍微写两行就能得到结论了,对于
n
≥
2
n\ge2
n≥2(n>=2,因为只有这样才能写出前一项n-1对应的概率值,是不是想起了高中做数列题的边界情况,没错这个问题其实就是一道亲切的数列题),有
p
(
n
)
=
1
n
∑
i
=
1
n
−
1
p
(
i
)
p(n)=\frac{1}{n}\sum_{i=1}^{n-1}p(i)
p(n)=n1∑i=1n−1p(i)
p
(
n
−
1
)
=
1
n
−
1
∑
i
=
1
n
−
2
p
(
i
)
p(n-1)=\frac{1}{n-1}\sum_{i=1}^{n-2}p(i)
p(n−1)=n−11∑i=1n−2p(i)
将下式代入上式,得到
p
(
n
)
=
1
n
∑
i
=
1
n
−
1
p
(
i
)
=
1
n
∑
i
=
1
n
−
2
p
(
i
)
+
1
n
∗
p
(
n
−
1
)
=
1
n
∑
i
=
1
n
−
2
p
(
i
)
+
1
n
∗
1
n
−
1
∑
i
=
1
n
−
2
p
(
i
)
=
(
1
n
(
n
−
1
)
+
1
n
)
∑
i
=
1
n
−
2
p
(
i
)
p(n)=\frac{1}{n}\sum_{i=1}^{n-1}p(i)=\frac{1}{n}\sum_{i=1}^{n-2}p(i)+\frac{1}{n}*p(n-1)=\frac{1}{n}\sum_{i=1}^{n-2}p(i)+\frac{1}{n}*\frac{1}{n-1}\sum_{i=1}^{n-2}p(i)=(\frac{1}{n(n-1)}+\frac{1}{n})\sum_{i=1}^{n-2}p(i)
p(n)=n1∑i=1n−1p(i)=n1∑i=1n−2p(i)+n1∗p(n−1)=n1∑i=1n−2p(i)+n1∗n−11∑i=1n−2p(i)=(n(n−1)1+n1)∑i=1n−2p(i)
这里用一下裂项,
1
n
(
n
−
1
)
+
1
n
=
1
n
−
1
−
1
n
+
1
n
=
1
n
−
1
\frac{1}{n(n-1)}+\frac{1}{n}=\frac{1}{n-1}-\frac{1}{n}+\frac{1}{n}=\frac{1}{n-1}
n(n−1)1+n1=n−11−n1+n1=n−11,则有,
p
(
n
)
=
(
1
n
(
n
−
1
)
+
1
n
)
∑
i
=
1
n
−
2
p
(
i
)
=
1
n
−
1
∑
i
=
1
n
−
2
p
(
i
)
p(n)=(\frac{1}{n(n-1)}+\frac{1}{n})\sum_{i=1}^{n-2}p(i)=\frac{1}{n-1}\sum_{i=1}^{n-2}p(i)
p(n)=(n(n−1)1+n1)∑i=1n−2p(i)=n−11∑i=1n−2p(i)
于是可以不停的代入不停的裂项,有
p
(
n
)
=
1
n
−
1
∑
i
=
1
n
−
2
p
(
i
)
=
1
n
−
2
∑
i
=
1
n
−
3
p
(
i
)
=
.
.
.
=
1
2
p
(
1
)
=
1
2
,
n
≥
2
p(n)=\frac{1}{n-1}\sum_{i=1}^{n-2}p(i)=\frac{1}{n-2}\sum_{i=1}^{n-3}p(i)=…=\frac{1}{2}p(1)=\frac{1}{2},n\ge2
p(n)=n−11∑i=1n−2p(i)=n−21∑i=1n−3p(i)=...=21p(1)=21,n≥2
于是得到
p
(
n
)
p(n)
p(n)的通项公式为,
p
(
n
)
=
{
1
,
n
=
1
1
2
,
n
≥
2
p(n)=\left\{ \begin{aligned} 1, n=1 \\ \frac{1}{2}, n\ge2 \end{aligned} \right.
p(n)=⎩⎨⎧1,n=121,n≥2
这是一个挺有意思的题目,当只有一个人时候,概率显然为1,当人数大于1时,结果始终为1/2,和人数n没有关系.
看到这个结论让我不禁对上述求解过程有了质疑,上述的求解过程又是一种”僵硬”的方法,所谓僵硬是指完全拿递推公式硬算出来的,应该是有一种更优雅的思路,能够直接得出结果为常数.暂时还没有想出来,等我想明白的时候再来更新吧.