- 随机过程本质就是一组与时间相关的随机变量,描述系统在 一系列时刻所处的状态。因此,我们首先补充关于多维随机变量(随机向量)的内容
- 注:本文中加粗大写字母代表矩阵(如
A
,
B
,
L
\pmb{A,B,L}
A,B,LA,B,LA,B,L) 或随机向量(如X
,
Y
\pmb{X,Y}
X,YX,YX,Y);加粗小写字母代表数的向量(如a
,
b
\pmb{a,b}
a,ba,ba,b);普通大写字母代表一个随机变量(如X
,
Y
X,Y
X,Y)
1. 多维 r.v. 的期望和方差
- 记多维 r.v.s. 为
X
=
[
X
1
X
2
⋮
X
n
]
,
Y
=
[
Y
1
Y
2
⋮
Y
n
]
\pmb{X} = \begin{bmatrix}X_1\\X_2\\\vdots \\X_n \end{bmatrix}, \pmb{Y} = \begin{bmatrix}Y_1\\Y_2\\\vdots \\Y_n \end{bmatrix}
XXX=⎣⎢⎢⎢⎡X1X2⋮Xn⎦⎥⎥⎥⎤,YYY=⎣⎢⎢⎢⎡Y1Y2⋮Yn⎦⎥⎥⎥⎤期望:E
X
=
[
E
X
1
E
X
2
⋮
E
X
n
]
E\pmb{X} = \begin{bmatrix}EX_1\\EX_2\\\vdots \\EX_n \end{bmatrix}
EXXX=⎣⎢⎢⎢⎡EX1EX2⋮EXn⎦⎥⎥⎥⎤方差(矩阵):
Var
(
X
)
=
(
Cov
(
X
i
,
X
j
)
)
n
×
n
=
(
E
[
(
X
i
−
E
X
i
)
(
X
j
−
E
X
j
)
]
)
n
×
n
=
E
[
(
X
−
E
X
)
(
X
−
E
X
)
⊤
]
\begin{aligned} \text{Var}(\pmb{X}) &= \big(\text{Cov}(X_i,X_j)\big)_{n\times n} \\ &=\big(E\big[(X_i-EX_i)(X_j-EX_j)\big]\big)_{n\times n} \\ &= E\big[(\pmb{X}-E\pmb{X})(\pmb{X}-E\pmb{X})^\top \big]\end{aligned}
Var(XXX)=(Cov(Xi,Xj))n×n=(E[(Xi−EXi)(Xj−EXj)])n×n=E[(XXX−EXXX)(XXX−EXXX)⊤]协方差(矩阵):
Cov
(
X
,
Y
)
=
(
Cov
(
X
i
,
Y
j
)
)
n
×
n
=
(
E
[
(
X
i
−
E
X
i
)
(
Y
j
−
E
Y
j
)
]
)
n
×
n
=
E
[
(
X
−
E
X
)
(
Y
−
E
Y
)
⊤
]
\begin{aligned} \text{Cov}(\pmb{X},\pmb{Y}) &= (\text{Cov}(X_i,Y_j))_{n\times n} \\ &=\big(E\big[(X_i-EX_i)(Y_j-EY_j)\big]\big)_{n\times n} \\ &= E\big[(\pmb{X}-E\pmb{X})(\pmb{Y}-E\pmb{Y})^\top\big] \end{aligned}
Cov(XXX,YYY)=(Cov(Xi,Yj))n×n=(E[(Xi−EXi)(Yj−EYj)])n×n=E[(XXX−EXXX)(YYY−EYYY)⊤]
- 方差矩阵性质:
Var
(
A
X
)
=
A
Var
(
X
)
A
⊤
\text{Var}(\pmb{AX}) = \pmb{A} \text{Var}(\pmb{X})\pmb{A}^\top
Var(AXAXAX)=AAAVar(XXX)AAA⊤,证明如下
Var
(
A
X
)
=
E
[
(
A
X
−
E
A
X
)
(
A
X
−
E
A
X
)
⊤
]
=
E
[
(
A
X
−
A
E
X
)
(
A
X
−
A
E
X
)
⊤
]
=
A
E
[
(
X
−
E
X
)
(
A
(
X
−
E
X
)
⊤
)
]
=
A
E
[
(
X
−
E
X
)
(
X
−
E
X
)
⊤
A
⊤
]
=
A
E
[
(
X
−
E
X
)
(
X
−
E
X
)
⊤
]
A
⊤
=
A
Var
(
X
)
A
⊤
\begin{aligned} \text{Var}(\pmb{AX}) &= E\big[(\pmb{AX}-E\pmb{AX})(\pmb{AX}-E\pmb{AX})^\top\big]\\ &= E\big[(\pmb{AX}-\pmb{A}E\pmb{X})(\pmb{AX}-\pmb{A}E\pmb{X})^\top\big]\\ &= \pmb{A}E\big[(\pmb{X}-E\pmb{X})(\pmb{A}(\pmb{X}-E\pmb{X})^\top)\big]\\ &= \pmb{A}E\big[(\pmb{X}-E\pmb{X})(\pmb{X}-E\pmb{X})^\top\pmb{A}^\top\big]\\ &= \pmb{A}E\big[(\pmb{X}-E\pmb{X})(\pmb{X}-E\pmb{X})^\top\big]\pmb{A}^\top\\ &=\pmb{A} \text{Var}(\pmb{X})\pmb{A}^\top \end{aligned}
Var(AXAXAX)=E[(AXAXAX−EAXAXAX)(AXAXAX−EAXAXAX)⊤]=E[(AXAXAX−AAAEXXX)(AXAXAX−AAAEXXX)⊤]=AAAE[(XXX−EXXX)(AAA(XXX−EXXX)⊤)]=AAAE[(XXX−EXXX)(XXX−EXXX)⊤AAA⊤]=AAAE[(XXX−EXXX)(XXX−EXXX)⊤]AAA⊤=AAAVar(XXX)AAA⊤ 说明:随机变量的线性组合仍是随机变量,对于一组随机变量,或者 “随机向量” 而言,可以对它们进行线性组合得到一个新的 “随机向量”,并用矩阵形式表示为A
r
×
n
X
n
×
1
=
X
r
×
1
′
\pmb{A}_{r\times n}\pmb{X}_{n\times 1} = \pmb{X}’_{r\times 1}
AAAr×nXXXn×1=XXXr×1′,即上式中A
X
\pmb{AX}
AXAXAX
2. 多维 r.v. 的分布函数
- 对于多维 r.v.s.(随机向量)
X
=
[
X
1
X
2
⋮
X
n
]
\pmb{X} = \begin{bmatrix}X_1\\X_2\\\vdots \\X_n \end{bmatrix}
XXX=⎣⎢⎢⎢⎡X1X2⋮Xn⎦⎥⎥⎥⎤,其分布函数定义为
F
(
X
)
=
F
(
X
1
,
X
2
,
.
.
.
,
X
n
)
=
P
(
X
1
≤
x
1
,
X
2
≤
x
2
,
.
.
.
,
X
n
≤
x
n
)
=
P
(
X
≤
x
)
F(\pmb{X}) = F(X_1,X_2,…,X_n) = P(X_1\leq x_1,X_2 \leq x_2,…,X_n\leq x_n) = P(\pmb{X} \leq \pmb{x})
F(XXX)=F(X1,X2,...,Xn)=P(X1≤x1,X2≤x2,...,Xn≤xn)=P(XXX≤xxx) - 两道例题
- 令
X
t
=
ξ
c
o
s
t
X_t = \xi cost
Xt=ξcost,其中P
(
ξ
=
1
)
=
P
(
ξ
=
2
)
=
P
(
ξ
=
3
)
=
1
3
,
t
∈
R
P(\xi=1)=P(\xi=2)=P(\xi=3)=\frac{1}{3},t\in\mathbb{R}
P(ξ=1)=P(ξ=2)=P(ξ=3)=31,t∈R,这样就可以通过选取不同的实数t
t
t 得到任意维随机向量{
X
t
}
\{X_t\}
{Xt}。求一维分布F
(
x
;
π
4
)
,
F
(
x
;
π
2
)
F(x;\frac{\pi}{4}),F(x;\frac{\pi}{2})
F(x;4π),F(x;2π) 和二维分布F
(
x
1
,
x
2
;
0
,
π
3
)
F(x_1,x_2;0,\frac{\pi}{3})
F(x1,x2;0,3π) - 令
X
t
=
ξ
+
η
t
X_t = \xi +\eta t
Xt=ξ+ηt,其中ξ
,
η
\xi,\eta
ξ,η 为互相独立的标准正态分布,t
∈
R
t\in\mathbb{R}
t∈R,这样就可以通过选取不同的实数t
t
t 得到任意维随机向量{
X
t
}
\{X_t\}
{Xt},求一维分布和二维分布
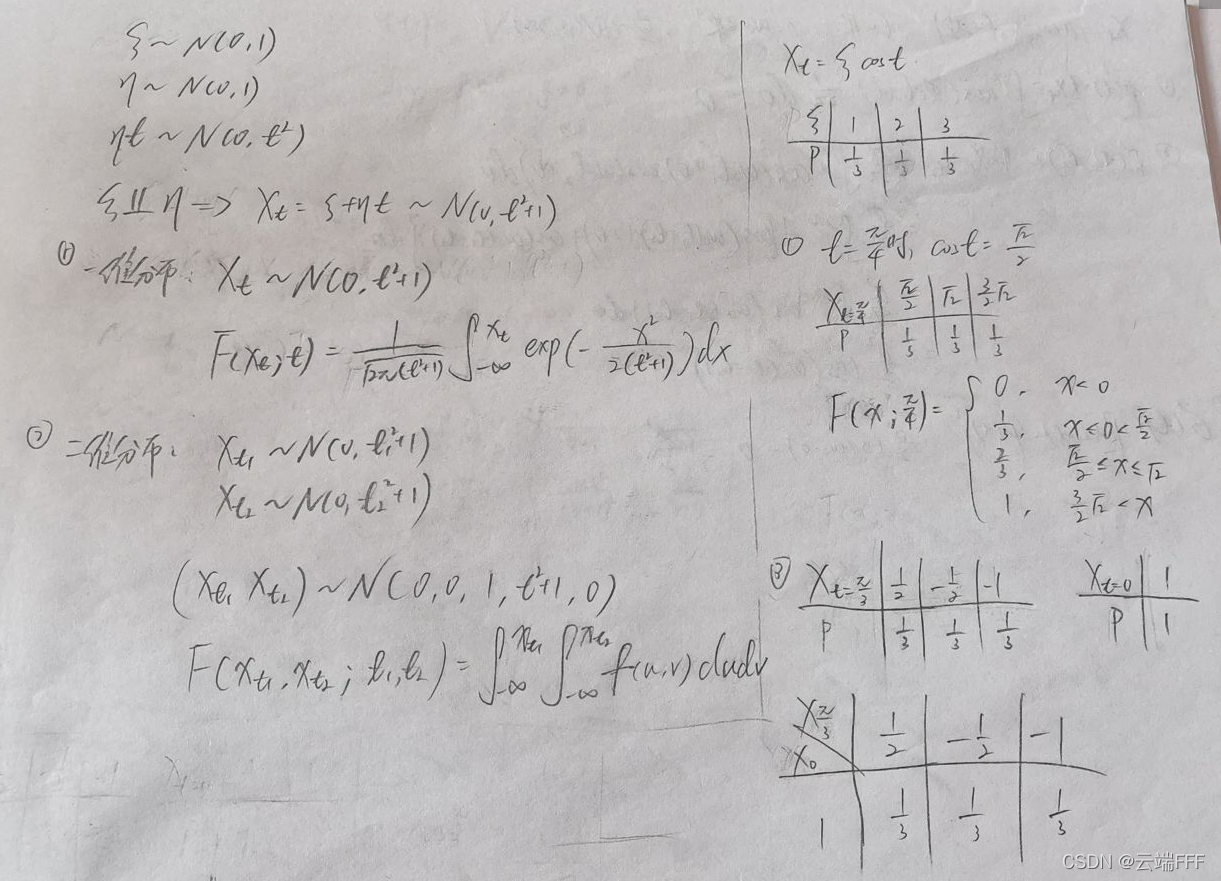
注:右边第1题答案中第3问,分布列应该是X
t
=
π
3
=
1
2
,
1
,
3
2
X_{t=\frac{\pi}{3}} = \frac{1}{2},1,\frac{3}{2}
Xt=3π=21,1,23,订正一下
- 令
3. 多维 r.v. 的函数(统计量)的概率密度
- 以二维情况为例,设二维 r.v.
X
=
(
X
1
,
X
2
)
\pmb{X}=(X_1,X_2)
XXX=(X1,X2) 的概率密度函数为
f
X
(
x
1
,
x
2
)
=
{
f
X
G
(
x
1
,
x
2
)
,
(
x
1
,
x
2
)
∈
G
⊂
R
0
,
(
x
1
,
x
2
)
∉
G
f_{\mathbf{X}}(x_1,x_2) = \left\{ \begin{aligned} &f_{\mathbf{X}}^G(x_1,x_2) &&,(x_1,x_2)\in G \subset \mathbb{R} \\ &0 &&,(x_1,x_2)\notin G\\ \end{aligned} \right.
fX(x1,x2)={fXG(x1,x2)0,(x1,x2)∈G⊂R,(x1,x2)∈/G 当有{
Y
1
=
g
1
(
X
1
,
X
2
)
Y
2
=
g
2
(
X
1
,
X
2
)
\left\{\begin{aligned}&Y_1 = g_1(X_1,X_2) \\&Y_2 = g_2(X_1,X_2) \end{aligned}\right.
{Y1=g1(X1,X2)Y2=g2(X1,X2) 时,求Y
=
(
Y
1
,
Y
2
)
\pmb{Y} = (Y_1,Y_2)
YYY=(Y1,Y2) 的概率密度函数f
Y
(
y
1
,
y
2
)
f_{\mathbf{Y}}(y_1,y_2)
fY(y1,y2) - 遵循以下过程求解
- 依题意,对于
X
1
,
X
2
X_1,X_2
X1,X2 的任意取值x
1
,
x
2
x_1,x_2
x1,x2,变换T
T
T 为
T
:
{
y
1
=
g
1
(
x
1
,
x
2
)
y
2
=
g
2
(
x
1
,
x
2
)
T:\left\{ \begin{aligned} &y_1 = g_1(x_1,x_2) \\ &y_2 = g_2(x_1,x_2) \end{aligned} \right.
T:{y1=g1(x1,x2)y2=g2(x1,x2) 利用变换T
T
T,把取值范围变换过来,即利用所有概率非0的(
x
1
,
x
2
)
(x_1,x_2)
(x1,x2) 找出所有概率非零的(
y
1
,
y
2
)
(y_1,y_2)
(y1,y2)
G
∗
=
T
(
G
)
G^* = T(G)
G∗=T(G) - 下面求
T
T
T 的反函数(即利用y
\pmb{y}
yyy 表示x
\pmb{x}
xxx),先假设有唯一的反函数
{
x
1
=
x
1
(
y
1
,
y
2
)
x
2
=
x
2
(
y
1
,
y
2
)
\left\{ \begin{aligned} &x_1 = x_1(y_1,y_2) \\ &x_2 = x_2(y_1,y_2) \end{aligned} \right.
{x1=x1(y1,y2)x2=x2(y1,y2) - 计算 Jacobi 行列式 (Jacobi 矩阵的行列式)
∣
J
∣
=
∣
∂
(
x
1
,
x
2
)
∂
(
y
1
,
y
2
)
∣
=
∣
∂
x
1
∂
y
1
∂
x
2
∂
y
1
∂
x
1
∂
y
2
∂
x
2
∂
y
2
∣
|\pmb{J}| = \begin{vmatrix} \frac{\partial(x_1,x_2)}{\partial(y_1,y_2)}\end{vmatrix} = \begin{vmatrix} \frac{\partial x_1}{\partial y_1} & \frac{\partial x_2}{\partial y_1} \\ \frac{\partial x_1}{\partial y_2} & \frac{\partial x_2}{\partial y_2} \end{vmatrix}
∣JJJ∣=∣∣∣∂(y1,y2)∂(x1,x2)∣∣∣=∣∣∣∣∣∂y1∂x1∂y2∂x1∂y1∂x2∂y2∂x2∣∣∣∣∣ 得到Y
=
{
Y
1
,
Y
2
}
\pmb{Y} = \{Y_1,Y_2\}
YYY={Y1,Y2} 的 p.d.f. 为
f
Y
(
y
1
,
y
2
)
=
{
f
X
G
(
x
1
(
y
1
,
y
2
)
,
x
2
(
y
1
,
y
2
)
)
∣
J
∣
,
(
y
1
,
y
2
)
∈
G
∗
0
,
(
y
1
,
y
2
)
∉
G
∗
f_{\mathbf{Y}}(y_1,y_2) = \left\{ \begin{aligned} &f_{\mathbf{X}}^G\big(x_1(y_1,y_2),x_2(y_1,y_2)\big) |\pmb{J}| &&,(y_1,y_2)\in G^* \\ &0 &&,(y_1,y_2)\notin G^*\\ \end{aligned} \right.
fY(y1,y2)={fXG(x1(y1,y2),x2(y1,y2))∣JJJ∣0,(y1,y2)∈G∗,(y1,y2)∈/G∗ - 若第 2 步中的反函数不唯一,则对每个反函数
x
(
i
)
\pmb{x}^{(i)}
xxx(i) 计算对应的 Jacobi 行列式∣
J
(
i
)
∣
,
i
=
1
,
2
,
.
.
.
,
n
|\pmb{J}^{(i)}|,i=1,2,…,n
∣JJJ(i)∣,i=1,2,...,n,最后得到Y
=
{
Y
1
,
Y
2
}
\pmb{Y} = \{Y_1,Y_2\}
YYY={Y1,Y2} 的 p.d.f. 为
f
Y
(
y
1
,
y
2
)
=
{
∑
i
=
1
n
f
X
G
(
x
1
(
i
)
(
y
1
,
y
2
)
,
x
2
(
i
)
(
y
1
,
y
2
)
)
∣
J
(
i
)
∣
,
(
y
1
,
y
2
)
∈
G
∗
0
,
(
y
1
,
y
2
)
∉
G
∗
f_{\mathbf{Y}}(y_1,y_2) = \left\{ \begin{aligned} &\sum_{i=1}^nf_{\mathbf{X}}^G\big(x_1^{(i)}(y_1,y_2),x_2^{(i)}(y_1,y_2)\big) |\pmb{J}^{(i)}| &&,(y_1,y_2)\in G^* \\ &0 &&,(y_1,y_2)\notin G^*\\ \end{aligned} \right.
fY(y1,y2)=⎩⎪⎪⎨⎪⎪⎧i=1∑nfXG(x1(i)(y1,y2),x2(i)(y1,y2))∣JJJ(i)∣0,(y1,y2)∈G∗,(y1,y2)∈/G∗
- 依题意,对于
- 例题:
-
设 r.v.s
{
X
,
Y
}
\{X,Y\}
{X,Y} 有
X
,
Y
∼
ϵ
(
1
)
X,Y\sim \epsilon(1)
X,Y∼ϵ(1) 且相互独立,对于如下线性变换,求
g
(
u
,
v
)
g(u,v)
g(u,v) 的 p.d.f
{
U
=
X
+
Y
V
=
X
/
Y
\left\{ \begin{aligned} &U = X+Y \\ &V = X/Y \end{aligned} \right.
{U=X+YV=X/Y 注意
X
,
Y
X,Y
X,Y 独立
⇔
F
X
,
Y
(
x
,
y
)
=
F
X
(
x
)
F
Y
(
y
)
\Leftrightarrow F_{X,Y}(x,y) = F_X(x)F_Y(y)
⇔FX,Y(x,y)=FX(x)FY(y),答案如下
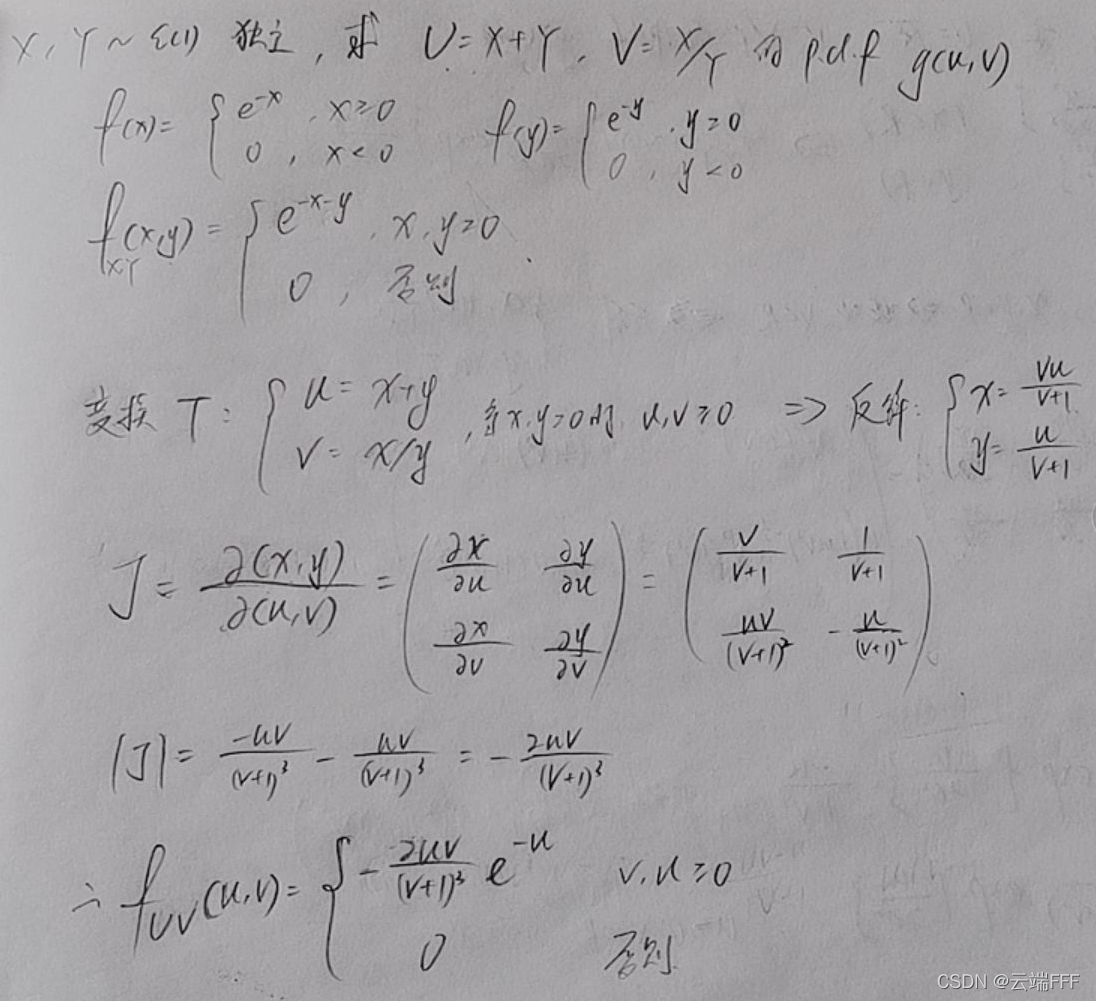
-
设 r.v.s
{
X
,
Y
}
\{X,Y\}
{X,Y} 有
X
,
Y
∼
N
(
0
,
σ
2
)
X,Y\sim N(0,\sigma^2)
X,Y∼N(0,σ2) 且相互独立,对于如下线性变换,求
g
(
u
,
v
)
g(u,v)
g(u,v) 的 p.d.f
{
U
=
X
2
+
Y
2
V
=
X
/
Y
\left\{ \begin{aligned} &U = \sqrt{X^2+Y^2} \\ &V = X/Y \end{aligned} \right.
{U=X2+Y2V=X/Y 注意
X
,
Y
X,Y
X,Y 独立
⇔
F
X
,
Y
(
x
,
y
)
=
F
X
(
x
)
F
Y
(
y
)
\Leftrightarrow F_{X,Y}(x,y) = F_X(x)F_Y(y)
⇔FX,Y(x,y)=FX(x)FY(y),答案如下
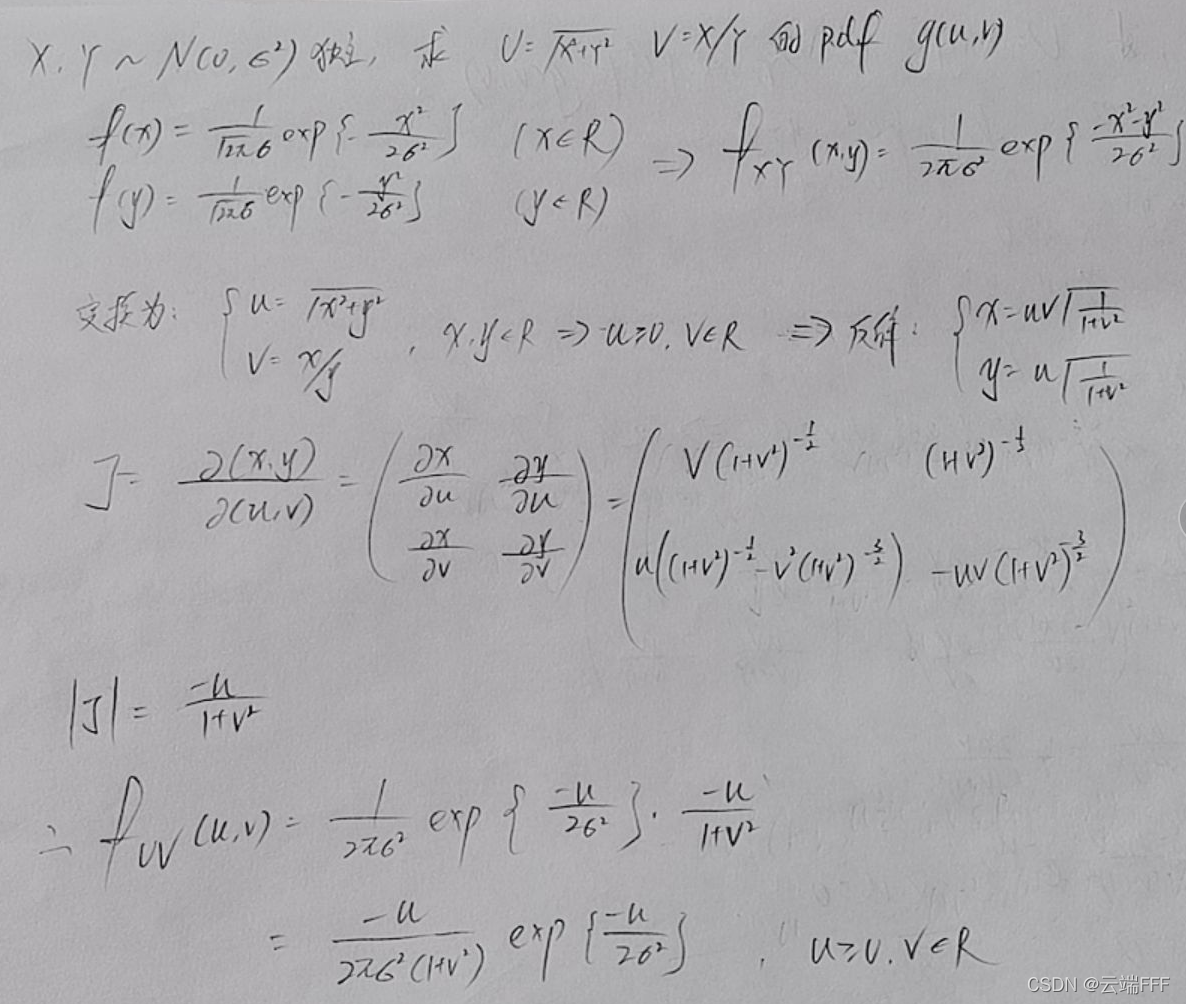
-