1,这节课的前半部分建立起KL公式,后一部分就在于建立随机过程的谱分析.
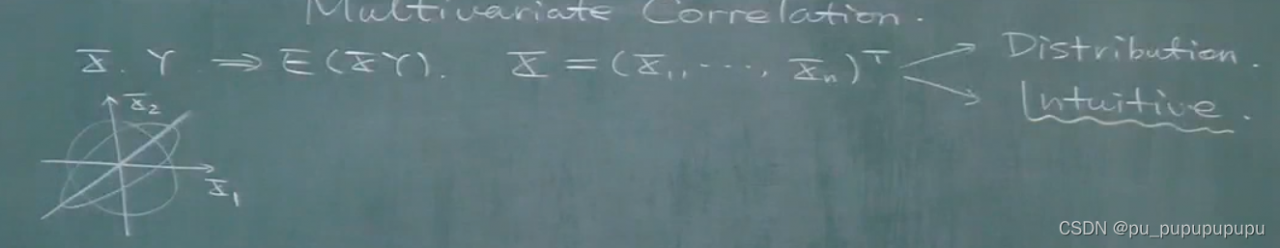
之前我妈研究的一直都是两个随机变量,现在来研究多维的随机变量,x定义为一个随机矢量,可以看成是一个随机过程截取一段.从分布和直观上把握.
对于二元随机变量,画出他们的联合分布,当联合分布退化为一条线的时候,就完全没有了随机性.但是不是一条线就有随机性了.
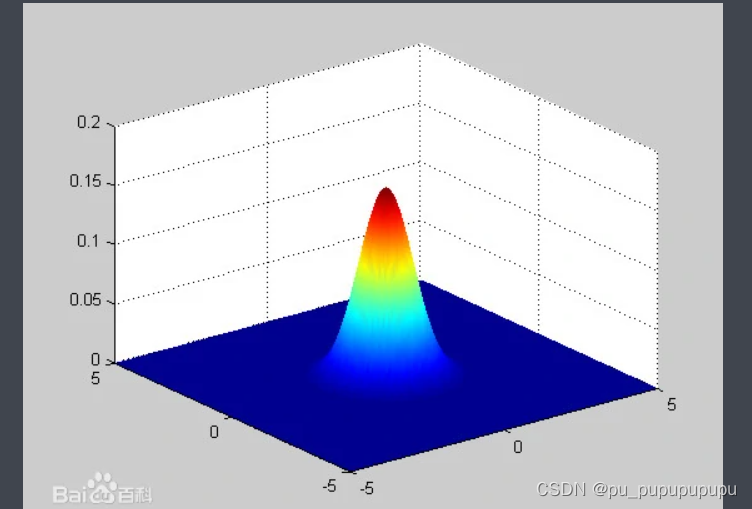
如上图为二维正态分布的图形.其中的纵轴表示的是概率密度.所以在之前的例子中都是等高线,也就是均匀分布的曲线.
但是对于多维随机矢量,我们无法想象其分布,就需要用直观的分析来取代其分析,就用之前提到的相关函数.
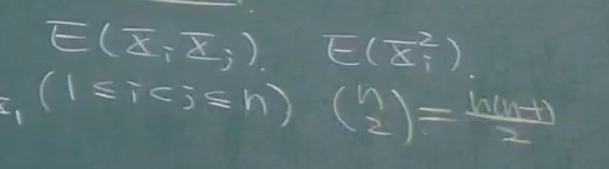
n维随机矢量,每两个随机变量之间都有一个相关值,那么一共有n×(n-1)/2个相关值,其中E(xi的平方)我们不考虑.这里注意相关值与相关函数的区别.我们可以通过相关函数取值得到任意一个相关值.
但是这些相关值并没有组织,我们还没建立起两个相关值之间的关系.
为了研究我们将其放在一个矩阵中,叫做相关矩阵

等于E(XX转置)
这个矩阵有几个特点,首先就是对称性,来自于期望的对称.
第二点,是正定的,相关阵都是正定的.(这里以宽平稳为例)
下面我们从三个不同的角度来,看这个矩阵的其他性质.
第一个角度:去相关(白化)

当这个矩阵为对角矩阵,就是任意一个随机变量都只与自身有相关性,与其他随机变量相关性都为0,这样的随机过程,我们叫做白谱.这种时候其功率谱是平的.所以我们想要找到一个矩阵A将原来的随机矢量,变成新的随机矢量y,并且其为对角矩阵.
我们要找到A矩阵.这个A将随机矢量各个分量的相关性消除了,也就是白化作用.
我们的未知数有n×n个,而结果只有n×(n-1)/2个结果(0)有效,因为另一半是对称的.
我们有如下分析
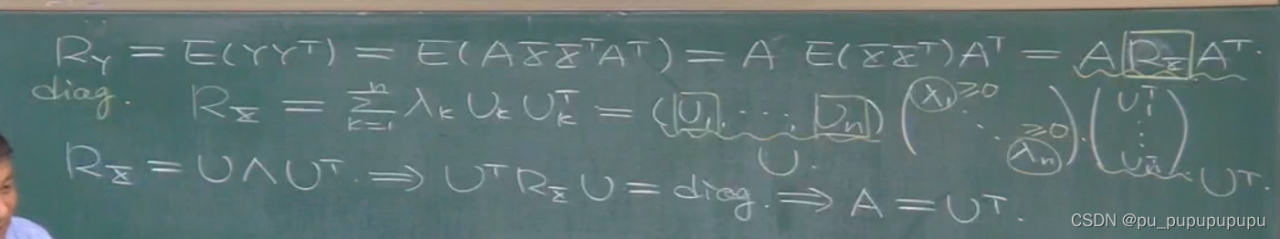
由于Rx为对称矩阵,所以可以用正交矩阵相似对角化,也就是u逆=u的转置.所以最后得到A=U的转置,u就是RX特征值的特征矩阵.注意这里A=u的转置
第二个角度:
主成分分析(pca)
在空间中找一些特征方向.
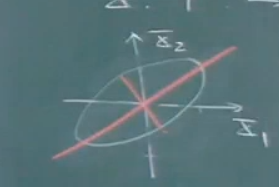
如上图,对纺锤进行简化,那么长的方向就代表信息的集中方向,而如果要简化模型,或者数据,就在短轴方向上进行抛弃,信息损失最小.
pca就是找到这些方向.(在我们手里没有上图的分布时,pca帮助确定方向.)
那么如何找到这些方向呢?
通过投影将多维的量进行降维,从而比较降维之后的结果.

或者说在长轴方向上方差最大.

投影公式如上.
在这个公式中,虽然α不知道,但是是确定量,而由于x的存在,所以投影为随机量.
知道了投影之后再来算方差.

其中E(x)为常数,所以主要还是看前面的一项.
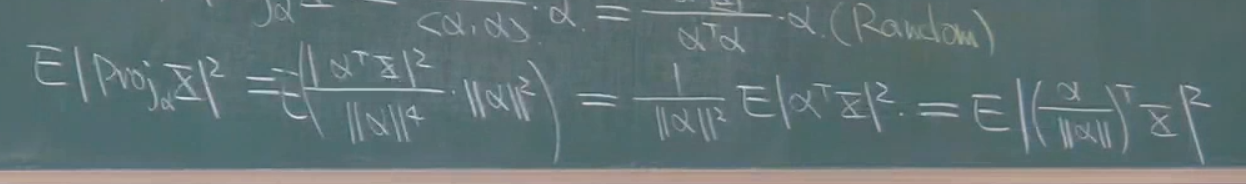
所以方差求得如上.最后一步相当于将(α的模归一化)之后转置×x的平方的期望.

所以我们要找最大值,并且具有限制条件就是α的模为1,用拉格朗日限制条件求解公式(原函数+lanmda(限制条件=0)),得到结果,这其中还有向量求导的知识,因为求导之后结果为(RX+RX转置)α,Rx为对称矩阵,所以为2RX.
所以就得到了 最大的方向,就是最大特征值对应得特征矢量方向.对应着主成分.
最短的方向,就是最小特征值所对应的特征矢量.
并且介于两者之间的特征值,也有对应的特征向量.这些特征向量在方向上相互垂直,第二大的特征值,对应方向一定垂直于最大方向,第三大的一定垂直于前两个方向构成的平面.
这里可以用主成分的思想解释特征矩阵为什么可以进行去相关化.
因为对称正定矩阵的特征向量相互正交.去相关化相当于将相关矩阵投影到各个垂直的方向.必然相互之间不相关.
pca主成分分析是最常用的降维手段.
图像压缩的基本思想.
首先一副图形之所以有信息,就在于一些像素点上产生了突变,并且一个像素点的突变是不够的,所以一个像素点发生了突变,那么在这个像素点开始的某一特定方向一定也有突变,这就产生了相关性.
图像压缩过程就是将图片看成一个排成方块的随机矢量,利用这些相关性,将图片适当缩小.
首先要做的,就是找到这个图片随机矢量的主成分,也就是去相关了,因为投影到了垂直的方向.把主成分留下,非主要成分压缩掉,这一步叫做变换编码.(有损)
对图像来说,扔掉的一般是细节.主要的轮廓会保存下来.

在实际操作过程中,可以将一张大的图片分成多个小图片来进行变换编码.并且在变换过程中,也不太使用pca方法,因为对每一个方块都要找相关矩阵的主成分.而改用DCT或DWT方法,就是离散(余弦)傅里叶变换或小波变换.
这两种变换就方便在,两种变化的基是预先做好的,与来波信号没关系.也就是前面的α,这里证明当图片维数足够大的情况下,两者是近似等价的.不需要每次都重新计算特征矢量.
变换编码之后就是运动编码,运动编码主要传递前后两帧图像的差异就好了.

所以可以大幅减少带宽.
第三步就是熵编码(无损),如RAR,zip,对应的可压缩大小也有限制.所以要先进行前面两步.
香农线:理论上编码的最高效率,图像编码还远远没有靠近.
例子:

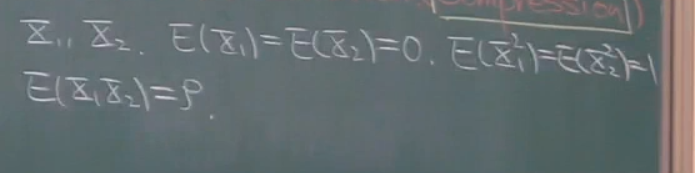
两个随机变量,均值为0,方差为1,并且相关系数不为0,那么其主成分的方向与x轴方向是否有关.
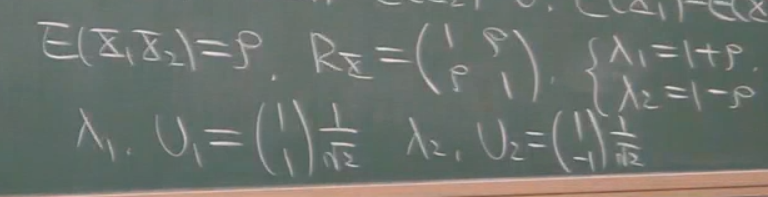
可以看出主成分方向与相关系数一点关系都没有.
那么相关系数到底决定什么?
相关系数决定的是纺锤的胖瘦.纺锤越瘦,相关系数越大,因为x1越能决定x2.
当相关系数为1,时就是线性.当相关系数为0时,退化为一个圆.这里注意之前的一个知识点,不相关不等于独立.
第二个问题,既然主成分方向与相关系数没关系,那到底和什么有关系?
两个随机变量的方差相等,那么主轴方向就是45度,要改变主轴方向就需要让两个方差不相等.也就是x轴投影与y轴投影不能相同(这里投影长短就代表方差),比值决定方向.
第三个角度:
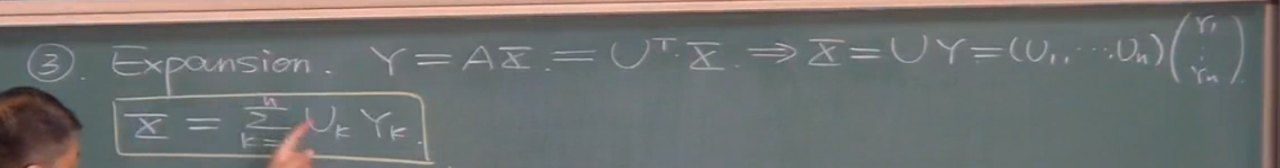
注意u的转置表示行向量组,x默认为列向量,所以这里得到一个n×1的y.
这里最终将x用U基的线性组合表示出来了,并且将x原本的两方面时间性与随机性进行了分离.在时间上从x1,到xn,并且其中每一个都是随机的.
时间上的变化分离到了Uk身上,而每一个x的随机性分离到了y身上.

并且展开的基是正交的,展开的系数在随机变量意义下也是正交的,因为是去相关的结果,所以这是一个双正交展开.
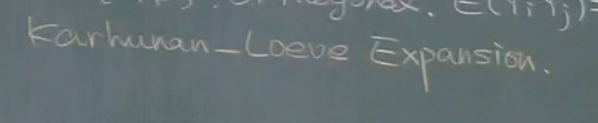
叫做如上展开(KL变换),并且这个展开并不要求x是一个宽平稳过程.
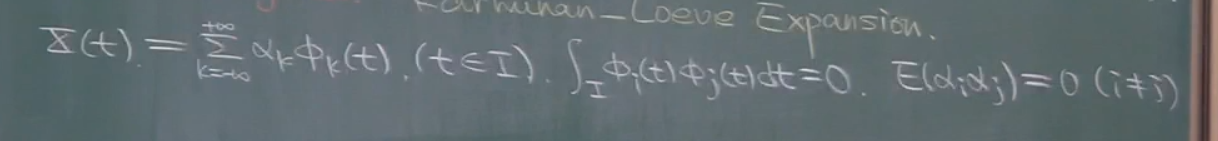
并且有连续时间的形式.之前的时间是1,2,3…n是离散的.k应该是维数.也是符合双正交展开的.
那么在连续时间中,如何求fai,特征向量的基呢?
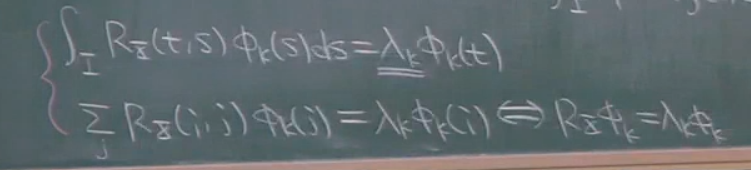
只是将原来的求和形式,变为了积分.这里要熟悉这种写法.并且只有方阵才说特征值,所以这里其实i,j是一样的.
这里的公式非常重要,我们将一个随机过程的随机性压缩在系数α中,将时间集中在了基当中.(t属于I)这里其实表示的是时间区间,也可以说是x的个数.
分界点.
那么如果这个x是宽平稳的随机过程,
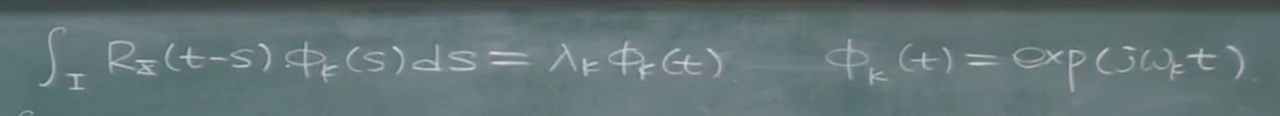
那么基就变成了复指数形式.
证明:
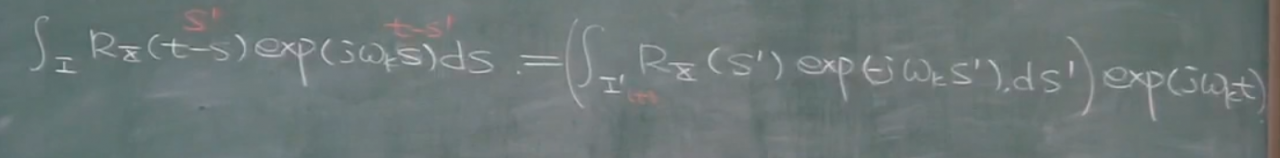
这里进行了换元t-s=s’,但是结果有一个问题就是,I’中与t是有关的,这使得我们无法积分,根据经验只要后面的函数为周期函数,那么就可以去掉t.
在随机过程的谱分析中,我们将确定性信号的傅里叶变换转换到随机信号的傅里叶变化时,发现的问题是,保证不了绝对可积.那时候我们用功率谱代替了一般的频谱.
其实还有一种方法,
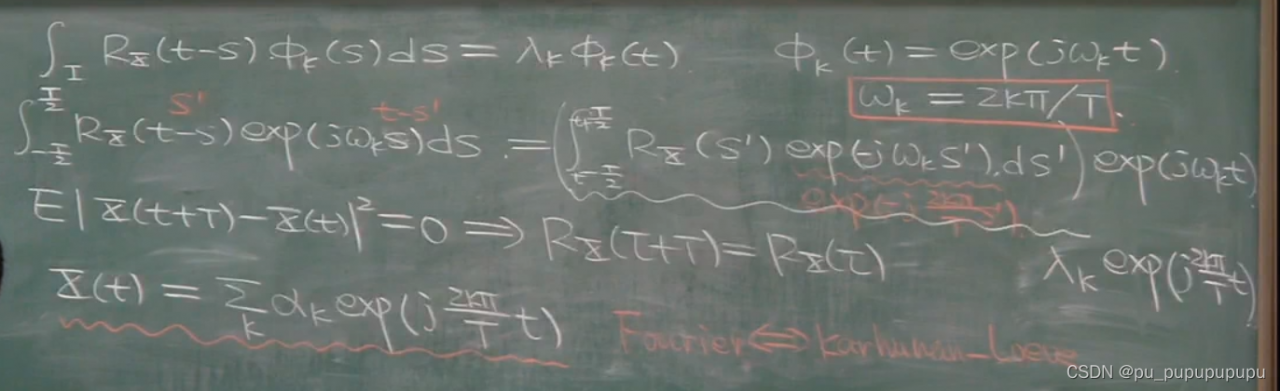
我们假定这个随机过程具有周期性T,并且是宽平稳随机过程,那么就可以说自相关函数是周期的.
并且假定是在一个周期中积分那么Rx(s’)exp(-jws’)就是周期的,前面说自相关函数是以T为周期,并且wk=2kpai/T也是周期的,所以乘起来是周期的,所以就与t没有关系了.
至此证明了周期宽平稳随机过程的特征矢量为e指数形式.
并且根据KL分解,为双正交的两部分,发现这就是傅里叶级数展开.傅里叶级数展开的复指数,就是相互正交的一组基.
并且我们还知道αk也是正交的,这里当然是针对随机函数来说,因为这里的正交是期望形式的正交.
之后我们令T趋于无穷大,这时候出现的问题就是αk是不太可能是收敛的
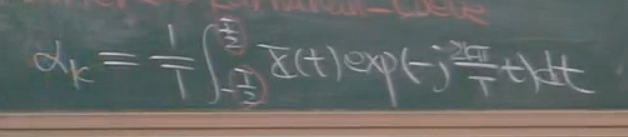
之前我们转向了自相关函数与功率谱,现在我们使用第二种方法.
我们换一种积分形式

一般的积分为dx,现在改为dg(x),那么积分就变成了
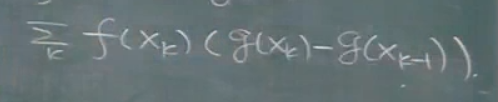
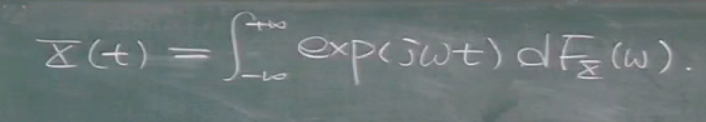
那么我们把x(t)写成如上形式,将有问题的X(w)放在d后面,不写出来就可以了,就认为是没有问题.这里应该是找到X(w)的原函数.这个就是谱表示方法.来处理随机过程的谱.
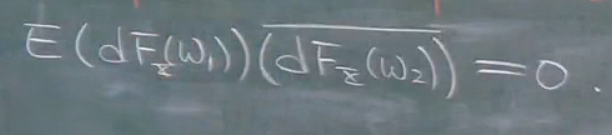
那么我们之前知道αk是正交的,所以我们新的表示方法就也是正交的.因为本质上相同.

那么在不同频点上做相关,就是正交增量过程,而在同一频点做相关,就是与功率谱密度有关.
下面证明,在同一频点的情况:
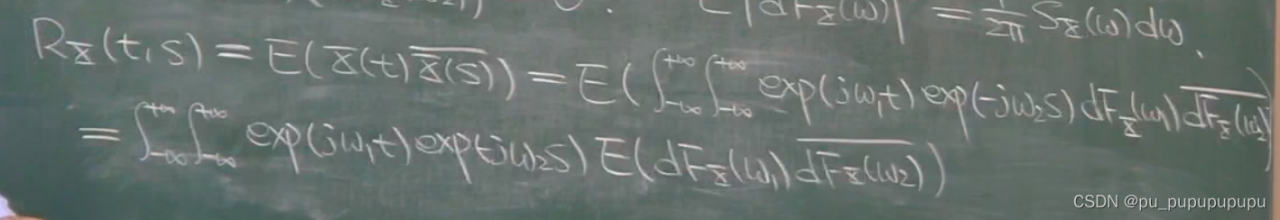
首先搞清楚随机性是在dF上面,因为这一部分就是前面的αk.
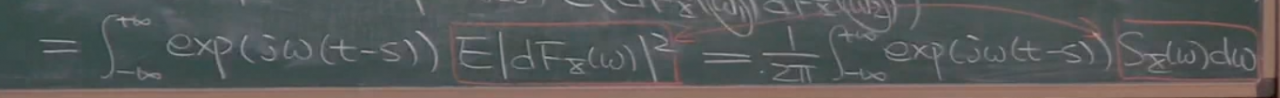
由于在同一频点上做积分,所以w1=w2,并且x(t)为宽平稳过程,所以可以写出其与功率谱密度的关系,就是最后一个式子,这样就会发现dF与功率谱密度是对应关系.
至此我们建立起了宽平稳随机信号的谱表示.而不再用功率谱代替了.并且回顾到我们的最开始问题,随机函数也就可以做傅里叶变换了.
那么对于一个随机过程过线性系统.我们进行分析
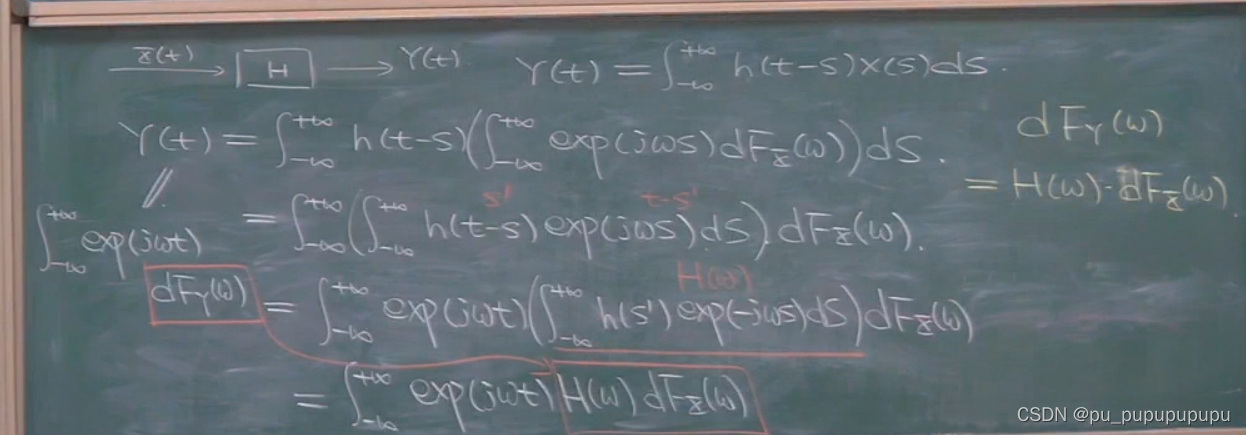
首先就是时域卷积,其次进行代换,我们通过换元操作,最后我们得到随机过程的谱就是dF与确定性信号的谱直接相关,都是乘以H(w),不同在于确定性信号的谱为X(w)而随机信号的谱不能d出来,写成dF的形式.
在上一节我们曾提到,过一个线性时不变系统,后频域等于其功率谱×H(w)模的平方,这里我们得到了另一种谱表示思路.
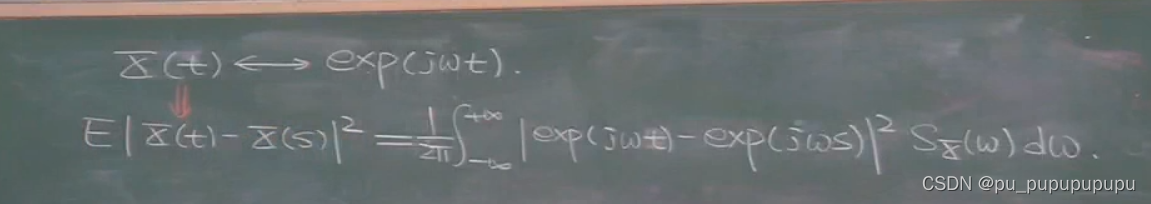
这里我们会发现宽平稳随机过程x(t),与复指数存在对应关系.
并且x(t)表示为均方距离,复指数表示为复指数的距离公式,这里没有解释公式从何而来.
这使得宽平稳随机过程x(t),居然可以与一个确定性的量,某种意义上画等号,叫做等距同构.在随机过程两个点的距离与复指数对应两个点之间的距离相同.
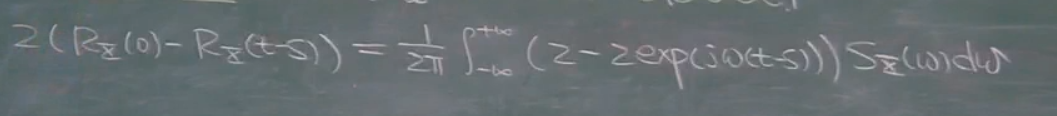
只需要将公式展开,结合功率谱与自相关函数转化公式,就可以证明.
随机变量是一个函数,但是在每一次实验中又是确定的.
![]()
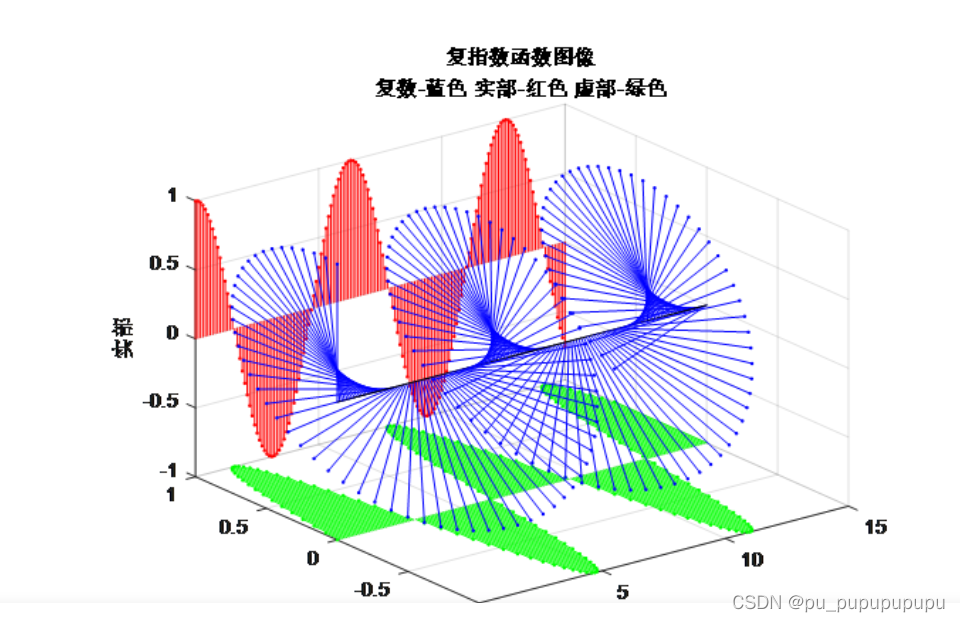
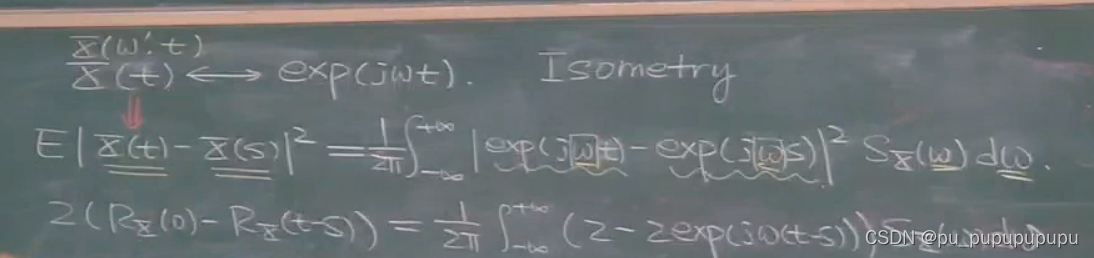
所以我们就可以把一个宽平稳随机过程看成是复指数函数.所以我们说宽平稳过程就需要震荡的,因为复指数函数不会有明显的趋势.
这里的衰减也只是初始量造成的.
所以我们之前的宽平稳过程,cos,电报信号,都是震荡的.
使得本来对我们神秘有很大不确定性的宽平稳随机过程,可以在一定程度上用确定的函数简单表示.