博客

之一：

【MATLAB】逐步搜索法、二分法、比例求根法、牛顿法、弦截法求方程的根

本文为《数值计算方法》的作业之二

之三：

1、欧拉法、2阶R-K法、4阶R-K法

x=1时解析解：

ans =

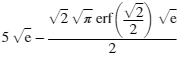
x=1时解析解约值:

ans = 6.8329

x=1,步长=0.1时欧拉解：

ans = 6.4053

x=1,步长=0.05时欧拉解：

ans = 6.6113

x=1,步长=0.01时欧拉解：

ans = 6.7872

x=1,2阶R-K法解：

ans = 6.8328

x=1,4阶R-K法解：

ans = 6.8329

% 分别使用欧拉法、2阶R-K法、4阶R-K法求解
% 步长分别选为0.1，0.05，0.01，并计算x=1时的函数值。对比你的 数值解与解析解
clear
% 解析解
syms y(x)
eqn = diff(y,x) == x * y - 1;
cond = y(0) == 5;
f_analysis = dsolve(eqn,cond);
disp("x=1时解析解：")
subs(f_analysis,1) % 符号变量赋值
disp("x=1时解析解约值:")
eval(subs(f_analysis,1))% 执行文本中的 MATLAB 表达式


% 欧拉法
h = 0.1;
[~,f_Euler] = Euler(0, 5, @(x,y)x*y-1, h, 1);
disp("x=1,步长=0.1时欧拉解：")
f_Euler(end)
h = 0.05;
[~,f_Euler] = Euler(0, 5, @(x,y)x*y-1, h, 1);
disp("x=1,步长=0.05时欧拉解：")
f_Euler(end)
h = 0.01;
[~,f_Euler] = Euler(0, 5, @(x,y)x*y-1, h, 1);
disp("x=1,步长=0.01时欧拉解：")
f_Euler(end)


% ode23    解非刚性微分方程，低精度，使用Runge-Kutta法的二三阶算法。
[~,y_RK2] = ode23(@(x,y) x * y - 1, [0 1], 5);
disp("x=1,2阶R-K法解：")
y_RK2(end)

% ode45    解非刚性微分方程，中等精度，使用Runge-Kutta法的四五阶算法。
[x,y_RK4] = ode45(@(x,y) x * y - 1, [0 1], 5);
disp("x=1,4阶R-K法解：")
y_RK4(end)


function [x, y] = Euler(x0, y0, f, h, x_right)
l = length(x0:h:x_right);
x = zeros(l,1);
y = zeros(l,1);
x(1) = x0;
y(1) = y0;
    for i = 1:(l-1)
        x(i + 1) = x(i) + h;
        y(i + 1) = y(i) + h * f(x(i),y(i));
    end
end

欧拉法与改进的欧拉法（预测-校准系统）

参考来源：《数值计算方法》第二版 高等教育出版社 2010第13次印刷（ISBN 978-7-04-012800-0） P97~101

clear

f = @(x,y) 1 ./(1+x^2) - 2.*y.^2
% 欧拉法h = 0.1;[x,f_Euler] = Euler(0, 0, @(x,y)f(x,y), h, 1);disp("x=1,步长=0.1时欧拉解：")f_Euler'
plot(x,f_Euler)
hold on
% 改进的欧拉法h = 0.1;[x,f_Euler] = Euler2(0, 0, @(x,y)f(x,y), h, 1);disp("x=1,步长=0.1时改进欧拉解：")f_Euler'
plot(x,f_Euler)hold off

function [x, y] = Euler(x0, y0, f, h, x_right)% 欧拉格式l = length(x0:h:x_right);x = zeros(l,1);y = zeros(l,1);x(1) = x0;y(1) = y0;    for i = 1:(l-1)        x(i + 1) = x(i) + h;        y(i + 1) = y(i) + h * f(x(i),y(i));    endend
function [x, y] = Euler2(x0, y0, f, h, x_right)% 改进的欧拉格式 预测-校准系统l = length(x0:h:x_right);x = zeros(l,1);y = zeros(l,1);x(1) = x0;y(1) = y0;    for i = 1:(l-1)        x(i + 1) = x(i) + h;        y_ = y(i) + h * f(x(i),y(i));% 预报        y(i + 1) = y(i) + h./2 .* (f(x(i),y(i)) + f(x(i),y_));% 矫正    endend

2、使用预测-校正法（M-S法、A-M法）

• M-S法结果：

ans = 1.8156e+16

• A-M法结果：

ans = 5.2682e+15

• 代码：

此部分代码部分参考

https://zhuanlan.zhihu.com/p/114288291

sys = MilneSimpson()
sys(end,2)
sys = AdamsMoulton()
sys(end,2)


function sys=MilneSimpson()

% MilneSimpson线性多步法求解常微分方程

    clear,clc,close all
 
    x1=0;
    x2=5;
    h=0.1;
    N=abs(x2-x1)/h; 
    y=zeros(N+1,1);
    x=zeros(N+1,1);
    y(1)=5;
    [~,y_RK4] = ode45(@(x,y) fx(x,y), [x1 x1+h], y(1));
    y(2)=y_RK4(end);
    [~,y_RK4] = ode45(@(x,y) fx(x,y), [x1 x1+2*h], y(1));
    y(3)=y_RK4(end);
    [~,y_RK4] = ode45(@(x,y) fx(x,y), [x1 x1+3*h], y(1));
    y(4)=y_RK4(end);
    
    
    x(1)=x1;
    for i=1: N
        x(i+1)=x1+i*h;
        if(i>=4)
            y(i+1)=y(i-3)+4*h/3*(2*fx(x(i),y(i))-fx(x(i-1),y(i-1))+2*fx(x(i-2),y(i-2)));
        end
        
    end
    sys(:,1)=x;
    sys(:,2)=y;
    
    draw(x,y)
end



function sys=AdamsMoulton()

% Adams-Moulton线性多步法求解常微分方程

    clear,clc,close all
 
    x1=0;
    x2=5;
    h=0.1;
    N=abs(x2-x1)/h; 
    y=zeros(N+1,1);
    x=zeros(N+1,1);
    y(1)=5;
    [~,y_RK4] = ode45(@(x,y) fx(x,y), [x1 x1+h], y(1));
    y(2)=y_RK4(end);
    [~,y_RK4] = ode45(@(x,y) fx(x,y), [x1 x1+2*h], y(1));
    y(3)=y_RK4(end);
    [~,y_RK4] = ode45(@(x,y) fx(x,y), [x1 x1+3*h], y(1));
    y(4)=y_RK4(end);
    
    
    x(1)=x1;
    for i=1: N
        x(i+1)=x1+i*h;
        if(i>=4)
            y(i+1)=y(i)+ h/24*(55*fx( x(i),y(i) )-59*fx( x(i-1) ,y(i-1)) +37*fx( x(i-2) ,y(i-2)) -9*fx( x(i-3) ,y(i-3)));
        end
    end
    sys(:,1)=x;
    sys(:,2)=y;
    
    draw(x,y)
end

function sys=fx(x, y)
    sys=x.^2.*y-x;
end

function draw(x,y)
    plot(x, y, '.-' )
    xlabel('X')
    ylabel('Y')
end

3、有限差分法

边值为y

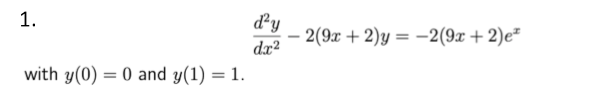
% 有限差分法finite difference method
clear
% 1 边值为y
% y'' + P(x)y' + Q(x)y = R(x)
P = @(x)(0);
Q = @(x)(-2*(9*x+2));
R = @(x)(-2*(9*x+2) * exp(x));
n = 100;
x_0 = 0;
x_n = 1;
y_x_0 = 0;
y_x_n = 1;
h = (x_n-x_0)/n;
x = x_0+h:h:x_n;

%Ax = B
A = zeros(n-1,n-1);
B = zeros(n-1,1);
for i = 1:(n-1)
    B(i) = h .^ 2 * R(x(i));
    if(i == 1)
        B(1) = B(1) - (1-h/2*P(x(i)))*y_x_0;
        A(1,1:2) = [h.^2*Q(x(i))-2 , (1+h/2*P(x(i)))];
    elseif(i == n-1)
        B(i) = B(i) - (1+h/2*P(x(i)))*y_x_n;
        A(i,end-1:end) = [(1-h/2*P(x(i))) , h.^2*Q(x(i))-2];
    else
        A(i,i-1:i-1+2) = [(1-h/2*P(x(i))) , h.^2*Q(x(i))-2 , (1+h/2*P(x(i)))];
    end
end

y = [y_x_0;A\B;y_x_n];
xx = [x_0,x]';
plot(xx,y,'.-')

边值为y’

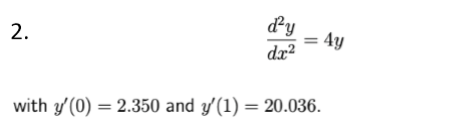
% 2 边值为y'
clear
% y'' + P(x)y' + Q(x)y = R(x)
P = @(x)(0);
Q = @(x)(-4);
R = @(x)(0);
n = 100;
x_0 = 0;
x_n = 1;
dy_x_0 = 2.350;
dy_x_n = 20.036;
h = (x_n-x_0)/n;
x = x_0-h:h:x_n+h;

%Ax = B 
A = zeros(n+3,n+3);
B = zeros(n+3,1);
for i = 1:(n+3)
    if(i == 1)
        B(1) = dy_x_0 * 2 * h;
        A(1,1:3) = [-1 0 1];
    elseif(i == n+3)
        B(i) = dy_x_n * 2 * h;
        A(i,end-2:end) = [-1 0 1];
    else
        B(i) = h .^ 2 * R(x(i));
        A(i,i-1:i-1+2) = [(1-h/2*P(x(i))) , h.^2*Q(x(i))-2 , (1+h/2*P(x(i)))];
    end
end

y = A\B;
xx = x';
plot(xx,y,'.-')