文章目录
1.二元分类(Binary classification)
二元分类问题,即训练样本的标签
y
∈
y\in
y
∈
{0,1},一般情况下:
- 0,表示负类(Negative class)
- 1,表示正类(Positive class)
1.1 逻辑回归的假设函数(Hypothesis function)
注意,逻辑回归模型虽然带着“回归”二字,但它是一个
分类
算法。
1.1.1 假设函数的推导
-
hθ
(
x
)
=
g
(
θ
T
x
)
h_θ(x)=g(θ^Tx)
h
θ
(
x
)
=
g
(
θ
T
x
)
-
g(
z
)
=
1
1
+
e
−
z
g(z) = \frac{1}{1+e^{-z}}
g
(
z
)
=
1
+
e
−
z
1
从而有:
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
h_θ(x) = \frac{1}{1+e^{-θ^Tx}}
h
θ
(
x
)
=
1
+
e
−
θ
T
x
1
注:
- g(z)被称为Sigmoid函数或者逻辑函数(Logistic function)
-
g(z)的图像如下

1.1.2 对假设函数输出的解释
h
θ
(
x
)
h_θ(x)
h
θ
(
x
)
= estimated probability that y = 1 on input x,即对于给定的输入向量x,根据选择的参数θ,计算输出变量y=1的估值概率(estimated probability),即
h
θ
(
x
)
h_θ(x)
h
θ
(
x
)
=P(y=1|x;θ)。
又因为在二元分类问题中
y
∈
y\in
y
∈
{0,1},有P(y=0|x;θ) + P(y=1|x;θ) = 1,进而:
P
(
y
=
0
∣
x
;
θ
)
=
1
−
P
(
y
=
1
∣
x
;
θ
)
P(y=0|x;θ) = 1 – P(y=1|x;θ)
P
(
y
=
0
∣
x
;
θ
)
=
1
−
P
(
y
=
1
∣
x
;
θ
)
1.1.3 决策边界(Decision boundary)
在逻辑回归中,我们预测:
{
y
=
1
,
当
h
θ
(
x
)
≥
0.5
y
=
0
,
当
h
θ
(
x
)
<
0.5
\begin{cases} y = 1,当h_θ(x)\ge0.5 \\ y = 0,当h_θ(x)<0.5 \end{cases}
{
y
=
1
,
当
h
θ
(
x
)
≥
0
.
5
y
=
0
,
当
h
θ
(
x
)
<
0
.
5
又因为
h
θ
(
x
)
=
g
(
θ
T
x
)
h_θ(x)=g(θ^Tx)
h
θ
(
x
)
=
g
(
θ
T
x
)
,结合Sigmoid函数的图像可知上述式子等价于
{
y
=
1
,
当
θ
T
x
≥
0
y
=
0
,
当
θ
T
x
<
0
\begin{cases} y = 1,当θ^Tx\ge0 \\ y = 0,当θ^Tx<0 \end{cases}
{
y
=
1
,
当
θ
T
x
≥
0
y
=
0
,
当
θ
T
x
<
0
下面举例来解释决策边界的概念:
-
例1:现在假设我们有一个模型:
hθ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
)
h_θ(x)=g(θ_0+θ_1x_1+θ_2x_2)
h
θ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
)
,且参数向量
θ=
[
−
3
1
1
]
θ=\begin{bmatrix} -3 \\ 1 \\ 1\end{bmatrix}
θ
=
⎣
⎡
−
3
1
1
⎦
⎤
则当
hθ
(
x
)
≥
0.5
h_θ(x)\ge0.5
h
θ
(
x
)
≥
0
.
5
,即
θT
x
≥
0
θ^Tx\ge0
θ
T
x
≥
0
,即
−3
+
x
1
+
x
2
≥
0
-3+x_1+x_2 \ge 0
−
3
+
x
1
+
x
2
≥
0
时,模型将预测y=1。
我们可以绘制直线
x
1
+
x
2
=
3
x_1+x_2=3
x
1
+
x
2
=
3
,这条线便是我们模型的分界线,称为
决策边界
,将预测为1的区域和预测为0的区域分隔开,如下图中红色的线即为我们这个例子的决策边界。

-
例2:非线性决策边界。
hθ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
+
θ
4
x
2
2
)
h_θ(x) = g(θ_0+θ_1x_1+θ_2x_2+θ_3x_1^2+θ_4x_2^2)
h
θ
(
x
)
=
g
(
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
+
θ
4
x
2
2
)
,且
θ=
[
−
1
0
0
1
1
]
θ=\begin{bmatrix} -1 \\ 0 \\ 0 \\ 1 \\ 1\end{bmatrix}
θ
=
⎣
⎢
⎢
⎢
⎢
⎡
−
1
0
0
1
1
⎦
⎥
⎥
⎥
⎥
⎤
(顺便提一下,这个模型是在前面提过的可以在特征中添加额外的高阶多项式,来使模型更好拟合数据。)
则当
hθ
(
x
)
≥
0.5
h_θ(x)\ge0.5
h
θ
(
x
)
≥
0
.
5
,即
θT
x
≥
0
θ^Tx\ge0
θ
T
x
≥
0
,即
−1
+
x
1
2
+
x
2
2
≥
0
-1+x_1^2+x_2^2 \ge 0
−
1
+
x
1
2
+
x
2
2
≥
0
时,模型将预测y=1。
同样地,我们可以绘制
x
1
2
+
x
2
2
=
1
x_1^2+x_2^2 = 1
x
1
2
+
x
2
2
=
1
,这条线便是我们模型的分界线,称为
决策边界
,将预测为1的区域和预测为0的区域分隔开,如下图中粉红色的线即为我们这个例子的决策边界。

注:
决策边界是假设函数的一个属性,由
h
θ
(
x
)
h_θ(x)
h
θ
(
x
)
与参数θ确定(即
θ
T
x
θ^Tx
θ
T
x
确定),并不会因数据集而改变;但是因为我们要使用数据集来拟合参数θ,故数据集会决定参数θ的取值;也就是说我们一旦有了确定的参数θ,决策边界就确定了。
1.2 逻辑回归的代价函数(Cost function)
1.2.1 回顾线性回归的代价函数
J
(
θ
)
=
1
m
∑
i
=
1
m
1
2
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(θ)=\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(h_θ(x^{(i)})-y^{(i)})^2
J
(
θ
)
=
m
1
∑
i
=
1
m
2
1
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
,为了方便理解,将此代价函数改写成如下形式:
{
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
1
2
(
(
h
θ
(
x
)
−
y
)
2
\begin{cases} J(θ)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_θ(x^{(i)}),y^{(i)})\\ Cost(h_θ(x),y) = \frac{1}{2}((h_θ(x)-y)^2 \end{cases}
{
J
(
θ
)
=
m
1
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
2
1
(
(
h
θ
(
x
)
−
y
)
2
如果在逻辑回归中继续使用线性回归的代价函数,
{
J
(
θ
)
h
θ
(
x
)
=
g
(
θ
T
x
)
=
1
1
+
e
−
θ
T
x
\begin{cases} J(θ)\\ h_θ(x)=g(θ^Tx)= \frac{1}{1+e^{-θ^Tx}} \end{cases}
{
J
(
θ
)
h
θ
(
x
)
=
g
(
θ
T
x
)
=
1
+
e
−
θ
T
x
1
,那么J(θ)就
变成了一个非凸函数(non-convex function),因此需要重新定义逻辑回归的代价函数。
1.2.2 基于单训练样本的逻辑回归代价函数
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
,
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
,
y
=
0
Cost(h_θ(x),y)=\begin{cases} \qquad-log(h_θ(x)),y=1 \\ \ -log(1-h_θ(x)),y=0 \end{cases}
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
,
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
,
y
=
0
,这样J(θ)就是一个凸函数。
下面我们根据图像来看一下我们的代价函数:
h
θ
(
x
)
h_θ(x)
h
θ
(
x
)
与
C
o
s
t
(
h
θ
(
x
)
,
y
)
Cost(h_θ(x),y)
C
o
s
t
(
h
θ
(
x
)
,
y
)
之间的关系如下图所示,横轴表示
h
θ
(
x
)
h_θ(x)
h
θ
(
x
)
,纵轴表示
C
o
s
t
(
h
θ
(
x
)
,
y
)
Cost(h_θ(x),y)
C
o
s
t
(
h
θ
(
x
)
,
y
)

y=1时,
{
若
h
θ
(
x
)
=
1
,
即
P
(
y
=
1
∣
x
;
θ
)
=
1
,
则
C
o
s
t
=
0
若
h
θ
(
x
)
→
0
,
即
P
(
y
=
1
∣
x
;
θ
)
→
0
,
则
C
o
s
t
→
∞
\begin{cases} 若h_θ(x)=1,\ 即P(y=1|x;θ)=1,\ 则Cost=0\\ 若h_θ(x)\to0,即P(y=1|x;θ)\to0,则Cost\to∞ \end{cases}
{
若
h
θ
(
x
)
=
1
,
即
P
(
y
=
1
∣
x
;
θ
)
=
1
,
则
C
o
s
t
=
0
若
h
θ
(
x
)
→
0
,
即
P
(
y
=
1
∣
x
;
θ
)
→
0
,
则
C
o
s
t
→
∞
y=0时,
{
若
h
θ
(
x
)
→
1
,
即
P
(
y
=
1
∣
x
;
θ
)
→
1
,
则
C
o
s
t
→
∞
若
h
θ
(
x
)
=
0
,
即
P
(
y
=
1
∣
x
;
θ
)
=
0
,
则
C
o
s
t
=
0
\begin{cases} 若h_θ(x)\to1,即P(y=1|x;θ)\to1,则Cost\to∞\\ 若h_θ(x)=0,\ 即P(y=1|x;θ)=0,\ 则Cost=0 \end{cases}
{
若
h
θ
(
x
)
→
1
,
即
P
(
y
=
1
∣
x
;
θ
)
→
1
,
则
C
o
s
t
→
∞
若
h
θ
(
x
)
=
0
,
即
P
(
y
=
1
∣
x
;
θ
)
=
0
,
则
C
o
s
t
=
0
1.2.3 逻辑回归代价函数的一般形式
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
J(θ)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_θ(x^{(i)}),y^{(i)})
J
(
θ
)
=
m
1
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
,
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
,
y
=
0
Cost(h_θ(x),y)=\begin{cases} \qquad-log(h_θ(x)),y=1 \\ \ -log(1-h_θ(x)),y=0 \end{cases}
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
,
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
,
y
=
0
,又因为在二元分类问题中y
∈
\in
∈
{0,1}(总是),
因此
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
l
o
g
(
1
−
h
θ
(
x
)
)
Cost(h_θ(x),y) = -ylog(h_θ(x))-(1-y)log(1-h_θ(x))
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
l
o
g
(
1
−
h
θ
(
x
)
)
,从而最终的代价函数的形式为:
J
(
θ
)
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
J(θ) = -\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_θ(x^{(i)}))+(1-y^{(i)})log(1-h_θ(x^{(i)}))]
J
(
θ
)
=
−
m
1
i
=
1
∑
m
[
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
1.3 批量梯度下降法(Batch Gradient Descent)
1.3.1 梯度下降法更新公式
Repeat until convergence{
θ
j
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
θ_j = θ_j – α\frac{\partial}{\partialθ_j}J(θ)(for \ j = 0,1,2,…,n+1)
θ
j
=
θ
j
−
α
∂
θ
j
∂
J
(
θ
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
}(同时更新所有
θ
j
θ_j
θ
j
)
将J(θ)带入上述更新公式中求出偏导数项,有:
Repeat until convergence{
θ
j
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
(
θ
)
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
θ_j = θ_j – α\frac{1}{m}\sum_{i=1}^{m}(h(θ)(x^{(i)})-y^{(i)})x_j^{(i)}(for \ j = 0,1,2,…,n+1)
θ
j
=
θ
j
−
α
m
1
i
=
1
∑
m
(
h
(
θ
)
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
}(同时更新所有
θ
j
θ_j
θ
j
)
其中,
θ
=
[
θ
0
θ
1
θ
2
⋮
θ
n
]
θ= \begin{bmatrix} θ_0 \\ θ_1 \\ θ_2 \\ \vdots \\ θ_n \end{bmatrix}
θ
=
⎣
⎢
⎢
⎢
⎢
⎢
⎡
θ
0
θ
1
θ
2
⋮
θ
n
⎦
⎥
⎥
⎥
⎥
⎥
⎤
注:
这里的更新公式与之前线性回归的更新公式表面上“看起来”完全一样,但是要注意
h
θ
(
x
)
h_θ(x)
h
θ
(
x
)
是不同的,
{
线
性
回
归
模
型
:
h
θ
(
x
)
=
θ
T
x
逻
辑
回
归
模
型
:
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
\begin{cases} 线性回归模型:h_θ(x)=θ^Tx\\ 逻辑回归模型:h_θ(x)=\frac{1}{1+e^{-θ^Tx}} \end{cases}
{
线
性
回
归
模
型
:
h
θ
(
x
)
=
θ
T
x
逻
辑
回
归
模
型
:
h
θ
(
x
)
=
1
+
e
−
θ
T
x
1
1.3.2 确保梯度下降法正常工作
如在线性回归模型中所讲,画出J(θ)关于迭代次数变化的函数图像,来看梯度下降法是否正常工作。
线性回归中提到的特征缩放,如果你的特征范围差距很大的话,那么应用特征缩放的方法,同样也可以让逻辑回归中,梯度下降收敛更快。
1.3.3 梯度下降法的向量形式
课上没有讲,自己暂时没有推导出来,先放在这里。
1.4 优化算法(Optimization algorithm)
使用优化算法时,那么我们需要做的是编写代码,当输入参数 θ 时,它们会计算出两样东西:
- J(θ)
-
∂∂
θ
j
J
(
θ
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
\frac{\partial}{\partial θ_j}J(θ)(for \ j = 0,1,2,…,n+1)
∂
θ
j
∂
J
(
θ
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
然后以梯度下降法为例,完成上述编码之后,就可以用梯度下降法的更新公式来更新参数θ,直至算法收敛:
Repeat until convergence{
θ
j
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
θ_j = θ_j – α\frac{\partial}{\partialθ_j}J(θ)(for \ j = 0,1,2,…,n+1)
θ
j
=
θ
j
−
α
∂
θ
j
∂
J
(
θ
)
(
f
o
r
j
=
0
,
1
,
2
,
.
.
.
,
n
+
1
)
}(同时更新所有
θ
j
θ_j
θ
j
)
优化算法,除了有梯度下降法之外,还有其他更
高级
的优化算法:
- Conjugate descent
- BFGS
- L-BFGS
对于这三种更高级的优化算法,它们的优缺点:
优点:
{
不
需
手
动
选
择
学
习
率
α
通
常
比
梯
度
下
降
法
收
敛
得
更
快
\begin{cases} 不需手动选择学习率α \\ 通常比梯度下降法收敛得更快 \end{cases}
{
不
需
手
动
选
择
学
习
率
α
通
常
比
梯
度
下
降
法
收
敛
得
更
快
缺点:比梯度下降法更加复杂一些。
对于以上三种高级优化算法,你并不需要去手写自己的优化算法,也不需要看懂源码,只需要会使用相应的库来实现即可。
2.多元分类(Multi-class classification)
多元分类又称为多类别分类(类别多于两个,即
≥
3
\ge3
≥
3
),即
y
∈
y\in
y
∈
{1,2,3…}(从0或者1开始都无所谓)。
通过“一对多”(one-vs-all)分类方法,就可以将逻辑回归分类器用在多类别分类问题上了。
“一对多”(或者说“一对余”)
分类方法的原理(举例子来讲解):
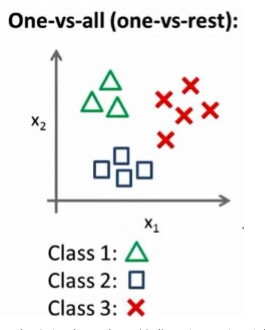
现在我们有一个训练集,好比上图表示的有三个类别,我们用三角形表示 y=1,方框表示 y=2,叉叉表示 y=3。我们下面要做的就是使用一个训练集,将其分成三个二元分类问题。
我们先从用三角形代表的类别 1 开始,实际上我们可以创建一个,新的”伪”训练集,类型 2 和类型 3 定为负类,类型 1 设定为正类,我们创建一个新的训练集,如下图所示的那样,我们要拟合出一个合适的分类器。
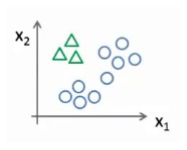
这里的三角形是正样本,而圆形代表负样本。可以这样想,设置三角形的值为 1,圆形的值为 0,下面我们来训练一个标准的逻辑回归分类器,这样我们就得到一个正边界。
为了能实现这样的转变,我们将多个类中的一个类标记为正向类(y=1),然后将其他所有类都标记为负向类,这个模型记作
h
θ
(
1
)
(
x
)
h^{(1)}_θ(x)
h
θ
(
1
)
(
x
)
。接着,类似地第我们选择另一个类标记为正向类(y=2),再将其它类都标记为负向类,将这个模型记作
h
θ
(
2
)
(
x
)
h^{(2)}_θ(x)
h
θ
(
2
)
(
x
)
,依此类推。
最后我们得到一系列的模型简记为:
h
θ
(
i
)
(
x
)
=
P
(
y
=
i
∣
x
;
θ
)
h^{(i)}_θ(x)=P(y=i|x;θ)
h
θ
(
i
)
(
x
)
=
P
(
y
=
i
∣
x
;
θ
)
,其中i=(1,2,3,…,k),k为类别数。

最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量。
总之,我们现在要做的就是训练这个逻辑回归分类器:
h
θ
(
i
)
(
x
)
h^{(i)}_θ(x)
h
θ
(
i
)
(
x
)
,其中 i 对应每一个可能的 y=i,最后,为了做出预测,我们给出输入一个新的 x 值,用这个做预测。我们要做的就是在我们三个分类器里面输入 x,然后我们选择一个让
h
θ
(
i
)
(
x
)
h^{(i)}_θ(x)
h
θ
(
i
)
(
x
)
最大的 i,即
m
a
x
i
h
θ
(
i
)
(
x
)
max_ih^{(i)}_θ(x)
m
a
x
i
h
θ
(
i
)
(
x
)
。
小结:
“一对多”分类方法就是:为每个类别i都训练一个逻辑回归分类器
h
θ
(
i
)
(
x
)
h^{(i)}_θ(x)
h
θ
(
i
)
(
x
)
,来预测y=i的概率;对一个给定的新的输入x,取
m
a
x
i
h
θ
(
i
)
(
x
)
max_ih^{(i)}_θ(x)
m
a
x
i
h
θ
(
i
)
(
x
)
作为新输入x的类别。