0 笔记说明
参考书籍为:

本篇博客是关于书中第八章的内容,下面开始即为正文。
1 书本内容
1.1 广义逆矩阵
1、
rank(A)≤rank(A
–
)
:因为rank(A)=rank(AA
–
A)≤rank(AA
–
)≤rank(A
–
)。
2、
减号逆的性质
:设A∈C
m×n
,λ∈R则:
(1) (A
T
)
–
=(A
–
)
T
,(A
H
)
–
=(A
–
)
H
;
(2) 若m=n,且rank(A)=n时,有A
–
=A
-1
,且此时A
–
唯一;
(3) (λA)
–
=λ
+
A
–
,其中λ∈R,λ
+
为:
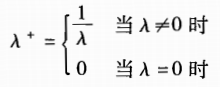
(4) 设S∈C
m×m
,rank(S)=m,T∈C
n×n
,rank(T)=n,且B=SAT,则(SAT)
–
=T
-1
A
–
S
-1
。
1.2 伪逆矩阵
1、
伪逆矩阵A
+
唯一
:证明:设X、Y都是A的伪逆矩阵,即X,Y都满足Penrose方程的四个等式,所以X=XAX=XAYAX=X(AY)
H
(АХ)
H
=X(AXAY)
H
=X(AY)
H
=XAY=XAYAY=(XA)
H
(YA)
H
Y=(YAXA)
H
Y=(YA)
H
Y=YAY=Y,证毕。
2、
加号逆的性质
:设A∈C
m×n
,λ∈R则:
(1) (A
T
)
+
=(A
+
)
T
,(A
H
)
+
=(A
+
)
H
;
(2) 若m=n,且rank(A)=n时,有A
+
=A
-1
;
(3) (λA)
+
=λ
+
A
+
,其中λ∈R,λ
+
为:
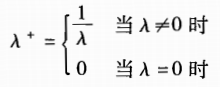
(4) 设S∈C
m×m
,rank(S)=m,T∈C
n×n
,rank(T)=n,且B=SAT,则(SAT)
+
=T
-1
A
+
S
-1
;
(5) (A
+
)
+
=A;
(6) (AA
H
)
+
=(A
H
)
+
A
+
=(A
+
)
H
A
+
,(A
H
A)
+
=A
+
(A
H
)
+
=A
+
(A
+
)
H
;
(7) A
+
=A
H
(AA
H
)
+
=(A
H
A)
+
A
H
。证明过程:A
+
=A
+
AA
+
=(A
+
A)
H
A
+
=A
H
(A
+
)
H
A
+
=A
H
(AA
H
)
+
,A
+
=A
+
AA
+
=A
+
(AA
+
)
H
=A
+
(A
+
)
H
A
H
=(A
H
A)
+
A
H
,证毕。
3、
对角矩阵的加号逆
:若A=diag(λ
1
,λ
2
,…,λ
n
),则A
+
=diag(μ
1
,μ
2
,…,μ
n
),其中μ
i
为:① λ
i
≠0时,μ
i
=λ
i
-1
;② λ
i
=0时,μ
i
=0。
1.3 广义逆与线性方程组
1、
相容方程组的最小模解
:相容方程组在一般情况下解是不唯一的,在这些解中,方程组的最小模解(或称最小范数解)在实际应用中是十分有用的。称相容方程组Ax=b的所有解x中模(2-范数)最小的解是Ax=b的最小模解,其中x的2-范数是||x||=sqrt(x
H
x)。设B是A∈C
m×n
的一个广义逆矩阵,则下列两个命题是等价的:
(1) 对于任给b∈R(A),则x=Bb一定是Ax=b的最小模解;
(2) (BA)
H
=BA。
2 听课笔记
2.1 广义逆矩阵
1、
矩阵的逆
:若A∈C
n×n
,且A为可逆矩阵,则:
① AA
-1
A=A;
② A
-1
AA
-1
=A
-1
;
③ (AA
-1
)
H
=AA
-1
;
④ (A
-1
A)
H
=A
-1
A。
2、
Penrose方程
:若A∈C
m×n
,以下矩阵方程称为Penrose方程:
① AXA=A;
② XAX=X;
③ (AX)
H
=AX;
④ (XA)
H
=XA。
满足Penrose方程中一个或多个的X∈C
n×m
称为A的一种广义逆矩阵,其中满足①的广义逆矩阵称为减号逆,记为A
–
,满足①②③④的广义逆矩阵称为加号逆,记为A
+
。教材上称减号逆A
–
为广义逆,称加号逆A
+
为伪逆。
3、
减号逆存在定理
:A∈C
m×n
,则减号逆A
–
一定存在,且不唯一。证明过程如下:

4、
减号逆的求解
:A∈C
m×n
,则:

举个栗子:矩阵A为:
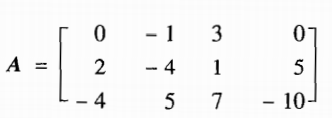
而:

故矩阵P、Q为:
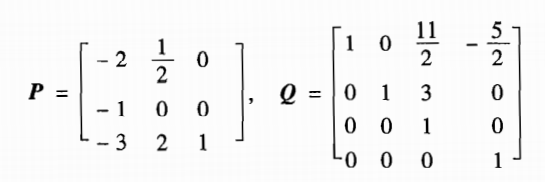
则:
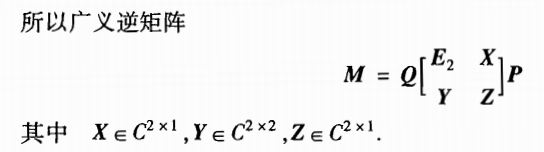
5、
矩阵的左逆与右逆
:设A∈C
m×n
:
(1)若存在矩阵B∈C
n×m
,使得BA=Ⅰ
n
,则称B是A的左逆,记A
L
-1
=B,称A左可逆;
(2)若存在矩阵B∈C
n×m
,使得AB=Ⅰ
m
,则称B是A的右逆,记A
R
-1
=B,称A右可逆;
(3)若A是满秩方阵,则A
-1
=A
L
-1
=A
R
-1
。
2.2 伪逆矩阵
1、
列满秩矩阵存在左逆
:设A∈C
m×n
,rank(A)=n,即A是列满秩矩阵,则A存在左逆,A
L
-1
=(A
H
A)
-1
A
H
。证明过程如下:

2、
行满秩矩阵存在右逆
:设A∈C
m×n
,rank(A)=m,即A是行满秩矩阵,则A存在右逆,A
R
-1
=A
H
(AA
H
)
-1
。证明过程如下:
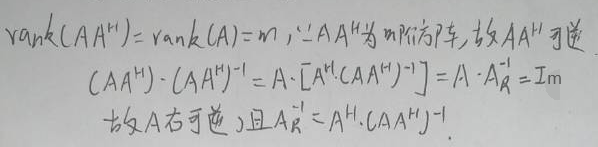
3、
加号逆存在定理
:设A∈C
m×n
,A=BC是A的一个满秩分解,其中B为列满秩矩阵,则B存在左逆,且B
L
-1
=(B
H
B)
-1
B
H
,C为行满秩矩阵,则C存在右逆,且C
R
-1
=C
H
(CC
H
)
-1
,则X=C
R
-1
·B
L
-1
=C
H
(CC
H
)
-1
(B
H
B)
-1
B
H
是A的加号逆A
+
,也称为伪逆矩阵。
2.3 广义逆与线性方程组
1、
相容非齐次线性方程组解的结构
:A∈C
m×n
,若Ax=b有解,则通解为x=A
–
b+(Ⅰ
n
-A
–
A)·t,其中Ⅰ
n
是n阶单位阵,t∈C
n
。显然Ax=b的通解等于Ax=0的通解加上Ax=b的一个特解。而x=A
–
b为Ax=b的一个特解,x=(Ⅰ
n
-A
–
A)·t为Ax=0的通解,代入验证确实是这样。
2、
非齐次线性方程组的相容性
:A∈C
m×n
,Ax=b有解⇔b=AA
–
b。证明过程如下:

3、
最小二乘解的通解
:A∈C
m×n
,b∈C
m
,则Ax=b的最小二乘解的通解为x=A
+
b+(Ⅰ
n
-A
+
A)·t,其中Ⅰ
n
是n阶单位阵,t∈C
n
。
END