判断一个数P是否为素数的一般方法:
方法1
:k从2开始,到n-1为止,判断P是否可以整除k
改进1
:k到sqrt(P)为止
改进2
:k从3开始且只考虑奇数
时间复杂度
:O(P)
一个更快的算法:Miller-Rabin算法
实现思路
:在2到P-1的范围内,随机选择一个数a,若a正好不满足
,就输出P不是质数;否则重复m次,若每次的a都满足上述公式,就输出P是质数。
时间复杂度分析
:m是一个不大的数,比如10;关键是计算
耗时。
利用到的定理和思想:
1.费马定理
:如果P是质数,一定有
因此,如果输出判断为不是质数,结果一定是对的。
反之则不一定成立,所以会出现不是质数却被判断为质数的情况。
2.定理:
如果P不是质数,则没有一个a或者至少在[2,P-1]中一半数的a,使得
不成立。
3.错误概率:
每次错误的概率不大于1/2,所以判定m次,错误概率不大于
。所以m越大的话错误概率就越小,最后是一个可接受的值,甚至可以忽略。
属于Monte-Carlo算法,牺牲了一定的正确率但是换来了时间上的高效。
python代码实现
import random
# 快速求幂取模
def quickPowMod(a,n,m):
re = 1
base = a % m
while(n>0):
tem = n&1
if (tem):
re = (re*base) % m
base = (base*base) % m
n >>= 1
return re
def Miler_Rabin(P):
# 循环次数m
m = 10
flag = 0
for i in range(0, m):
# a是2-P-1的随机数
a = random.randint(2, P-1)
# 直接求幂取余
# tem = pow(a, P-1)
# tem2 = tem % P
# 快速求幂取余
tem2 = quickPowMod(a,P-1,P)
if tem2 != 1:
flag = 1
break
if flag == 0:
print("{0} is prime".format(P))
elif flag == 1:
print("{0} is not prime".format(P))
else:
print("error")
if __name__ == '__main__':
while(1):
P = int(input("请输入一个数字:"))
Miler_Rabin(P)
数据测试(添加了两个测试函数)
import random
import time
# 快速求幂取模
def quickPowMod(a,n,m):
re = 1
base = a % m
while(n>0):
tem = n&1
if (tem):
re = (re*base) % m
base = (base*base) % m
n >>= 1
return re
def Miler_Rabin(P):
# 循环次数m
m = 10
flag = 0
for i in range(0, m):
# a是2-P-1的随机数
a = random.randint(2, P-1)
# 直接求幂取余
# tem = pow(a, P-1)
# tem2 = tem % P
# 快速求幂取余
tem2 = quickPowMod(a,P-1,P)
if tem2 != 1:
flag = 1
break
if flag == 0:
print("{0} is prime".format(P))
elif flag == 1:
print("{0} is not prime".format(P))
else:
print("error")
# 对素数进行判定,同时还能验证算法正确率
# prime,prime2中都是素数
def test1():
prime = [9998581,9999071,9999163,9999167,9999217,9999221,9999397,9999713,9999929,9999991]
prime2 = [111111111111229,111111111111233,111111111111389,111111111111443,111111111111527,519111111111683,719111111111683,919111111111553,919111111111679,919111111111681]
sumTime = 0
maxTime = 0
for P in prime2:
start = time.time()
Miler_Rabin(P)
end = time.time()
timeUse = end-start
if maxTime < timeUse:
maxTime = timeUse
sumTime = sumTime+(timeUse)
print("平均用时{0}s".format(sumTime/len(prime)))
print("最坏用时{0}s".format(maxTime))
# 对随机数进行判断
def test2():
sumTime = 0
maxTime = 0
for i in range(0,100):
P = random.randint(100000000000000000000000000000,999999999999999999999999999999)
start = time.time()
Miler_Rabin(P)
end = time.time()
timeUse = end-start
if maxTime < timeUse:
maxTime = timeUse
sumTime = sumTime+(timeUse)
print("平均用时{0}s".format(sumTime/100))
print("最坏用时{0}s".format(maxTime))
if __name__ == '__main__':
test1()
test2()
实验结果:
对10个9位素数判断的平均用时和最坏用时如下:
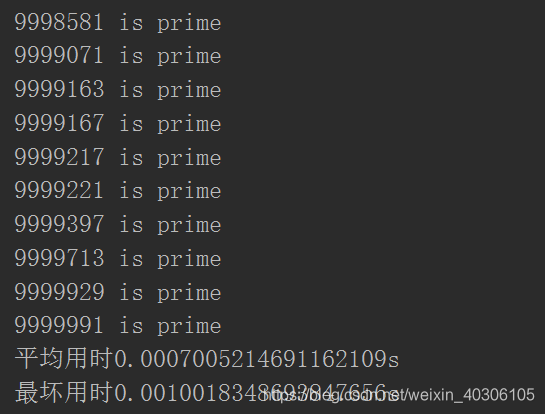
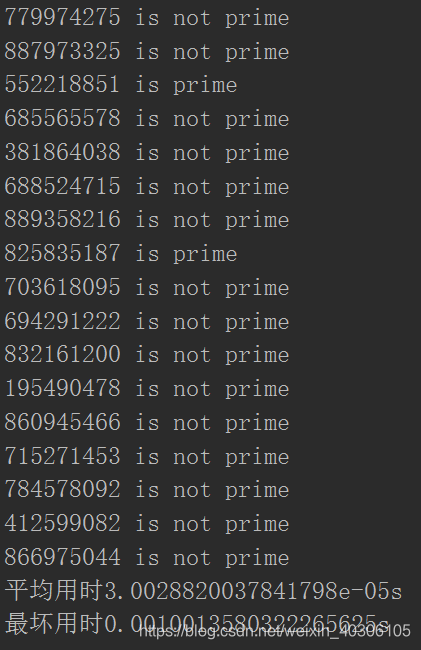
对100个随机的9位数进行素数判断,耗时情况如下:
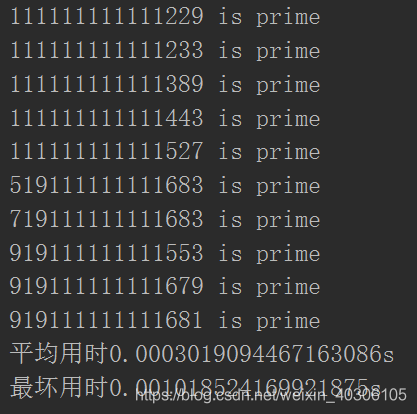
对10个12位素数的判断平均用时和最坏用时如下:
对100个随机的12位数进行素数判断,耗时情况如下:
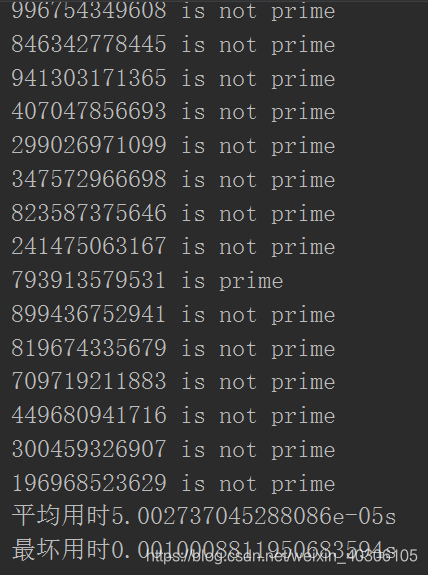
对100个随机的30位数进行素数判断,耗时情况如下:
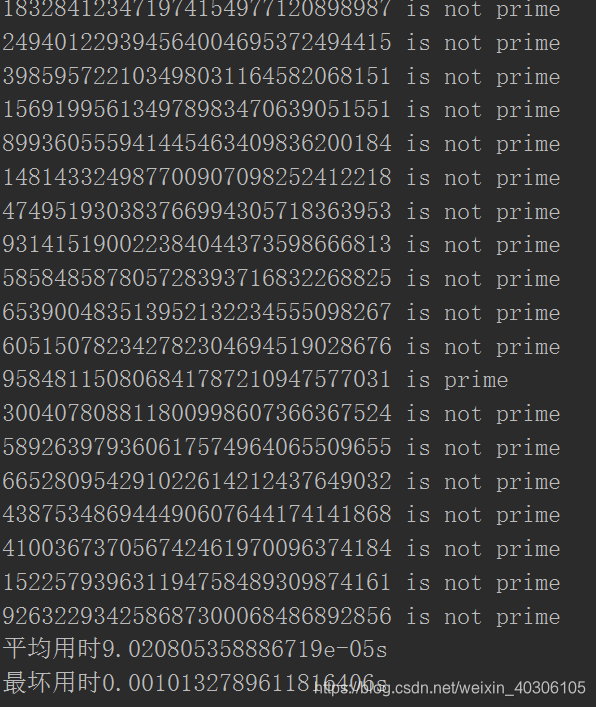
结论
使用Miller-Rabin算法来判断素数的正确率非常高,这一点也可以通过提高判断次数m来做到。通过对实验数据的分析,可以看到对9、12、30位的数进行判断,最坏用时都是相近的(被判断的数中有素数),这是因为使用了快速求幂取余的方法,判断素数的过程都是m轮计算量相近的求幂取余运算。