这节课的内容主要讲速度的正向运动学(也就是位置的一阶导数,所以叫一阶运动学)和静力学,这也是本书首次出现动力学相关的内容(刚体运动那节提到的力旋量算是一个概念的介绍)。
个人结合平时的工程项目看,觉得这节课的内容是一个内容和难度上的一个跨越,因此适合反复的去研读这节课的内容。
引入:平面机器人速度运动学与静力学
平面机器人速度运动学
课程从平面2R机器人引入,机器人的正向运动学是根据一个前向运动学函数,输入关节角度θ,通过FK函数f,得到末端位置x。那么f对时间求导,就是先对θ求导,再由θ对时间t求导(就是关节角速度),所以链式法则的结果就是,
关节速度左乘雅可比矩阵,得到末端速度
。因此
雅克比矩阵本质就是FK函数对关节角求导。
雅可比矩阵的第i列表示,当到达某位形时,i轴的关节角速度为1,其他关节速度为0时候的末端速度。
假设只有两个关节,关节的速度有正负之分,假设它在横纵坐标的分布下来是一个矩形,其实雅可比矩阵左乘它,就是就是对它进行了一个线性变换,那么得到了一个反映为末端速度的平行四边形。
同样如果限制所有关节速度的模长为1,那么就不再是矩形了,而是一个圆。这个圆经过线性变换得到反映为末端速度的椭圆,就是所谓的
可操作度椭球
。假如关节完全向右侧打直了,那么可操作度椭球就变成了一条竖线,它就到了
奇异位形
。
奇异位形表现为雅可比矩阵变成奇异阵(即秩不是满秩)。椭球的长短半径可以看出它是接近奇异位形还是远离奇异位形。
平面机器人静力学:
什么叫静力学呢?这个后面其实有讲到:
关节处的功率消耗= 用于机器人运动的功率消耗 + 末端执行器功率消耗
既然是静力学,意思就是关节速度目前其实是0,那么就没有用于机器人运动的功率消耗。。所以关节的功率消耗就等于末端执行器的功率消耗。
有一些书中直接提到的概念,我个人认为需要提前解释:
虚功原理:
对于一个静态平衡的系统,所有外力作用,经过
虚位移
,所作的
虚功
,总和为0。
虚功:
位移与做功无关的其他因素引起,此时力作的功为虚功,那么这段经过的位移叫
虚位移。
(我已经不记得这块的内容是不是多年前的初中讲过了,虽然表面上说的很复杂,其实一句话即可表明:比如在一个绝对光滑的平面,有一个小物块在匀速滑动,那么它的位移就是和做功无关的其他因素引起的,这就是虚位移。这时你突然从上方施加了一个垂直向下的压力,那么没有摩擦力,所以不能对小物块减速,小物块仍然滑动,那么你上方施加的这个力,其实就是作的虚功。)
力矩:
力矩定义很简单,力乘以力臂即为力矩。
ps:但是力矩这个概念,说实话最开始我是比较陌生的,因此刚开始做机械臂的时候,随口问出这个问题,什么是力矩?结果感觉领导似乎非常鄙视我,说这是中学知识点,问我高考怎么考上大学的?还开玩笑让HR去查我的学信网文凭。
我当时觉得非常丢人,但是想来想去我真的不记得这个概念。但是我自认自己高中的时候又不是学渣,所以我特意查了一下(强行挽尊),人教版高中物理有两本必修,选修课本有1-1,1-2,2开头的有三本,2-1到2-3,3开头的有5本,3-1到3-5。普通高中开头的都是3开头的选修课,而实际上力矩的概念出现在高中物理选修2-2课本中,2开头的是职高的课本。。我上的又不是职高,那我怎么能知道呢?后来本科学了电子信息,研究生干了计算机,更是不接触力学的东西了。不过,不知道毕竟不是什么光彩的事情,人要知耻,赶紧补上就是了。
(今天回头看,这个问题作为一个机器人工程师,问的真是很愚蠢,也很感谢当时的领导,卡内基梅隆的唐博士没有直接开掉我,给了我一点学习的时间,hh)
力矩的范围比较宽泛,一切力乘以力臂的结果都可以称为力矩。而与此同时还有
扭矩
和
转矩。
转矩是使得物体发生转动的一种特殊的力矩,一个物体在转矩的作用下,可能会产生扭转变形,因此在大多数领域其实扭矩和转矩不严格区分。那么在对于转动副关节,也不区分力矩、扭矩和转矩的概念。
关节功率:关节力矩乘以关节角速度称之为关节功率。单位也和功率相同
。
末端功率为末端力乘以末端速度,关节功率为关节力矩乘以关节角速度,这二者相等,因此可以继续推下去,把上面得到的末端速度等于雅可比矩阵乘以关节角速度代入,得到结论是:
关节力矩 = 雅可比矩阵
的
转置
乘以
末端力。
力椭球:反映机器人生成不同方向力的难以程度。它和可操作度椭球的关系是主轴方向相同,但是长度相反。那么当奇异位形的时候,可操作度椭球变成了一条直线,力椭球变成了和它正交的一条无限长的直线。
比如向下拉着一桶水,胳膊完全竖直,那么这时候就是奇异位形,因为丢失了朝下的自由度。但是这时能提供的力是最大的,关节直接承力,肌肉不再承力,理论上讲你能承受无限大的重量(当然力太大,你的关节会被拉坏)
到现在为止,事实上速度运动学和静力学的概念就讲完了,后续的内容只不过就是把它从平面2R机器人,挪到了3维空间中。
机器人雅可比
前面已经说过:
雅可比矩阵的第i列表示,在到达某位形时,当i轴的关节角速度为1,其他关节速度为0时候的末端速度。
那么在空间机器人中,其实第i列,表示的是:在到达某位形时,当i轴关节角速度
而其他关节速度为0时的运动旋量
。
空间雅可比
直接整理为:
雅可比矩阵的计算方式:
和FK
【现代机器人学】学习笔记三:前向运动学(Forward Kinematics)_zkk9527的博客-CSDN博客
中类似, 先把机器人
依次从1轴开始
,摆到某个位形(
在FK中是0位,这里则不是零位
),然后根据坐标系的朝向写出下一个轴(第i轴)的w,然后把轴上一点q也写出来,使用
写出v,或者直接根据移动副写出v,令w为0。这样就写出来就是雅可比中的i列。
1.对于第一轴,和FK中算螺旋轴旋量的方法一样。
2.对于当前的w和q,要考虑进去前面的旋转和平移,可以写成变量的形式。
过程可以再跟着书上的例题走一遍,这里不赘述。
那么具体该怎么才能得到这个雅可比矩阵呢?参考书中的公式:

我们只要跟着这个公式,就可以得到雅可比矩阵。代码实现则可以参考:
物体雅可比
这里的做法则是和FK那节的也很像,
其实可以理解为把末端当成了固定系,
先从最后一个轴依次开始转,依次按照末端坐标系写w和v,仿照空间雅可比的部分,一个一个摆到对应位形,写出雅可比矩阵的列。最后得到的雅可比就是物体雅可比。同样,一般形式的雅可比也要写成变量的形式,因为各个轴的角度不固定。
具体的实现过程同理:

我们只要跟着这个公式,就可以得到雅可比矩阵。代码实现则可以参考:
空间雅可比与物体雅可比的几何解释
这节的内容,书上叨叨叨啰啰嗦嗦写了一堆,一眼看过去,特么的看的人头都大了。
我用很简单的话总结一下:
比如:
,这玩意是描述了个啥呢?
其实就是先保持
和
的姿态,其他关节角度为0,假设这个姿态是s”系,然后看3关节相对于这个s”系的旋量,然后再用伴随矩阵映射回最开始的S系。
如果你看懂了我的这句话,读懂这一篇的内容相信就是非常容易了。
空间雅可比与物体雅可比的关系
一个公式解释:
和旋量的转换一样,因为雅可比矩阵的每一列本质上就是旋量。
解析雅可比与几何雅可比
旋量的就是几何雅可比,因为关节角速度左乘了雅可比得到的是一个旋量。
而机器人领域并不是所有人都用旋量,不用旋量也一样可以搞机器人,那么末端真实的,在space系下线速度和角速度如何呢?
回忆一下,旋量前三维是角速度,后三维是线速度,但是这个
线速度实际上是末端做运动时,假设有个无限大的刚体,这个刚体“刚好过space系原点的那个位置处”的线速度
。参见
【现代机器人学】学习笔记二:刚体运动_zkk9527的博客-CSDN博客
那么比如我司,末端减速怎么做的呢?我看了一下代码,用的就是关节角度左乘雅可比,得到的就是末端在space系下的速度,即前三维是xyz在space系下的线速度,rpy是space系下的角速度(这种表示更为直观),然后把这个速度每个控制周期做一个衰减,结合时间积分,加到末端笛卡尔系下面,这样保持末端的平稳减速。
所以这种
广义速度坐标,
需要的雅可比,就是解析雅可比。
转换关系我列出来(
纯粹是因为我记不住,等着以后现用现查
):
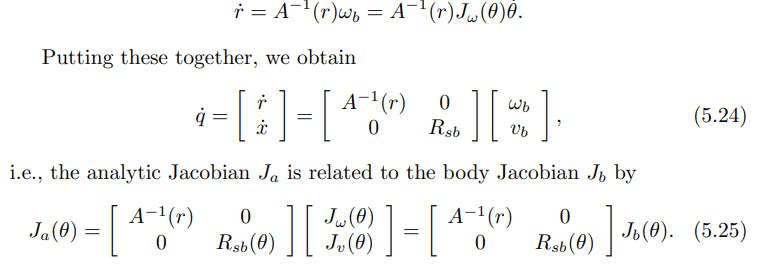
其中,
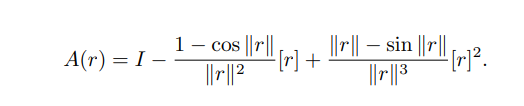
![]()
则为我们熟知的旋转部分的轴角表示法。
ps:发现有些好笑的一点,搞技术的人是有点固执的,宁可承认有人用的是这种解析雅可比,也绝不愿意违背自己一向的原则。我们可以发现,这个
里面,仍然是旋转在前,平移在后。。实际上使用解析雅可比的人,已经是先强调位置,后强调朝向了。
逆向速度运动学
逆向意味着根据末端算关节,这是下一节课的内容:
【现代机器人学】学习笔记五:逆运动学(Inverse kinematics)
这节提到的内容:
关节数:n=6且满秩,则雅可比矩阵可逆,则容易根据关节角速度求出末端速度。
但是n不是6,或者机器人奇异的时候,雅可比矩阵不可逆。n<6则机器人不能实现任意的末端速度,n>6为
冗余
机器人,n-6个自由度不能反映到机器人末端。剧透:n=6,机器人逆解的数量为有限个,而n>6,机器人逆解为无穷多个,因此可以做避障之类的用途。
一下就想起了几个概念:
欠驱动
系统是指系统的
独立控制变量个数
小于
系统自由度个数
的一类非线性系统
过驱动
系统是一类控制输入数多于输出数的系统。(其实就是上面 “小于”换成 “大于”,换种说法)相同的则叫
完全驱动。
开链机器人的静力学
开链机器人又叫串联机器人,就是指这个运动链中没有环路。
这个前面其实已经讲过了:
末端功率为末端力乘以末端速度,关节功率为关节力矩乘以关节角速度,这二者相等,因此可以继续推下去,把上面得到的末端速度等于雅可比矩阵乘以关节角速度代入,得到结论是:
关节力矩 =
雅可比矩阵的
转置
乘以
末端力。
那么拿到空间机器人静力学这里,就是:
关节力矩与关节角速度相乘,等于力旋量与旋量相乘。力旋量参见
【现代机器人学】学习笔记二:刚体运动_zkk9527的博客-CSDN博客
那么把旋量等于雅可比乘以关节角速度带入,得到:
这里力旋量
可以是body系也可以是space系的,只不过要和前面的雅可比对应(物体雅可比或空间雅可比)
注意,这里的
雅可比是转置的形式!
力旋量在body和space系下的变换,也是遵循“下标内反外转置”,参见笔记二节。不要记混了。这里可以这样辅助理解;反映末端力的难易程度的力椭球和反映末端速度的可操作度椭球刚好是相反的状态,容易做速度的,就不容易做力,所以使用雅可比矩阵的时候要记得用转置的形式。
n如果小于6,那么在6-n的力旋量空间也不会产生力,例如门把手只有一个旋转关节,那么它只能产生一个与门把手圆周运动相切的力,同时抵制其他五维力旋量空间的任意力旋量。
奇异性分析
这节的内容至关重要,学完可以说是受益匪浅,
建议记死记牢,平时一定是会用到的。
运动学奇异的发生与坐标系的选择无关。
以下五种情况必然会发生运动学奇异:
2个旋转关节共轴
共轴则雅可比矩阵两个列相同,当然不会满秩了。
3个旋转关节轴线平行
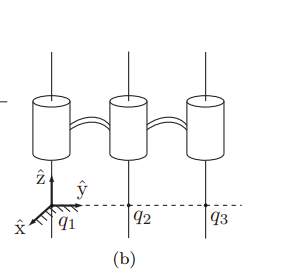
这样雅可比矩阵中3个w都相同,v是-w叉乘q,q在同一个线上,同一个w叉乘同一个方向的q必然得到一个方向相同的向量v,所以这三列必然线性相关。
4个旋转关节轴线共点
这个就太好想象了,假如共点在基坐标系原点,那么q可以取0,这样雅可比矩阵的四个列,全是只有3维w的螺旋轴旋量,那么4列只有三个数,当然会有一列是其他三列的线性表示了,所以这种情况也必然是奇异。
4个旋转关节轴线共面
这个比较隐蔽,但我司的机器人现在刚好就容易出现这个问题。恕我不能把图放上来,因为目前机器人还在研发阶段。
假如关节轴都在xy平面,那么w就没有z这方向的值了,只有两个数。
那么v,-wxq,这个q在轴上,肯定没有z值,这样得到的v必然也只有第三维。
所以雅可比矩阵的四个列,每个列的形式都一样,但是都只有三个未知数,必然奇异。
6个旋转关节轴线与一条线相交
假如都和基坐标系的z轴相交,那么每个q都可以取(0,0,qz),这样v=-wxq,v的第三维必然是0,所以雅可比矩阵最后一行全是0,这个雅可比矩阵一看就不满秩,当然奇异。
可操作度
可操作度椭球
这一章的内容也是啰啰嗦嗦一堆,其实实际上没说什么重要内容。
大意就是,我们根据可操作度椭球的概念(所有关节速度的模长为1),使用雅可比的逆左乘末端速度q,一番骚操作:
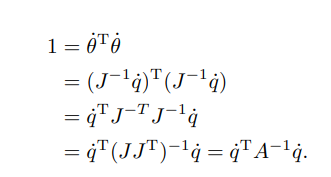
得到一个
,当雅可比J是满秩的,A就是对称正定阵。
正定矩阵:
方阵并且所有顺序主子式大于0
对称正定阵:所有特征值均为正。
有一个性质:若Q为正定阵,对于任意
,

回到书中 :
把线速度和角速度分开,因为量纲不同。
椭球的主轴方向为特征向量,主轴半径长为
根号下特征值。
有如下几种方式判断可操作度椭球的好坏:
1.A的最大特征值和最小特征值比例开根号,接近1则
各向同性
,意味着机器人沿哪个方向的速度都一样容易。奇异位则接近无穷大,因为最小特征值几乎没有了,可操作度椭球变成一条线了。
2.直接最大特征值比最小特征值,也是和1比。这个叫
条件数,用于衡量矩阵与向量相乘以后的敏感度程度。
这个好像是研究生数值分析课程的内容,意味着,如果向量有一点点误差偏差,经过矩阵相乘后,和真实值的偏差大小。这个内容当时肯定是学了,可惜当时学了白学,不知道有什么用,都还给老师了。毕业多年时隔今日才知道,真是唏嘘不已。回头等我有时间把数值分析好好总结一下。
3.计算可操作度椭球的体积。方法是算矩阵的行列式开根号,也可以用所有特征值相乘开根号。
这种情况是越大越好,因为奇异位可能特征值为0,直接这里就变成0了。
力椭球
和可操作度椭球类似,不过力的部分,也是和速度部分是反的。
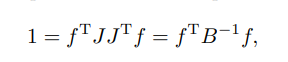
因此多了一个矩阵B,
的特征向量是A的特征向量,但是特征值值是A特征值的逆,即倒数。这也解释了为什么力椭球和可操作度椭球方向一致,但是主轴长度相反。
总结:
是可操作度椭球的,
是力椭球的。
增加可操作度椭球的体积,会同时减小力椭球体积。
下节再见!