博客

二叉树的三种遍历方式代码实现

二叉树遍历方式：先序、中序、后续遍历以及层次遍历，这里主要描述前面三种方式

先序遍历

遍历过程：

1. 访问根节点
2. 先序遍历左子树
3. 先序遍历右子树

例如：下图的遍历结果为

ABDFECGHI

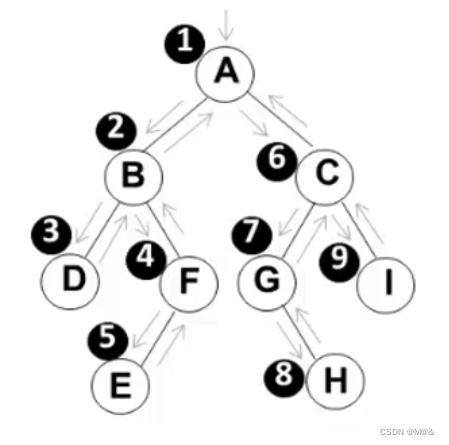
编码实现

1.利用函数递归实现

void PreOrderTraversal(BinTree BT){
      if(BT){
        printf("%5d",T->Data);//输出节点
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
      }
}

2.非递归函数实现，例如堆栈

void PreOrderTraversal(BinTree BT)
{
    BinTree T=BT;
    Stack S = CreatStack( Maxsize );//创建并初始化对战S
    while( T || !IsEmpty(S) ){
        while(T){ //一直向左并将沿途的节点压入堆栈
            Push(S,T);
            printf("%5d",T->Data);//输出节点
            T = T->Left;
        }
        if(!IsEmpty(S)){
            T = Pop(S);//弹出堆栈
            T = T->Right;//向弹出节点转向其有节点做一样操作
        }
    }
}

中序遍历

遍历过程：

1. 中序遍历左子树
2. 访问根节点
3. 中序遍历右子树

例如：下图的遍历结果是

DBEFAGHCI

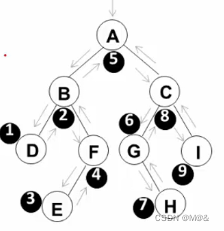
编码实现

1.利用函数递归实现

void InOrderTraversal(BinTree BT){
      if(BT){
        InOrderTraversal(BT->Left);
        printf("%5d",T->Data);//输出节点
        InOrderTraversal(BT->Right);
      }
}

2.非递归函数实现，例如堆栈

void InOrderTraversal(BinTree BT)
{
    BinTree T=BT;
    Stack S = CreatStack( Maxsize );//创建并初始化对战S
    while( T || !IsEmpty(S) ){
        while(T){ //一直向左并将沿途的节点压入堆栈
            Push(S,T);
            T = T->Left;
        }
        if(!IsEmpty(S)){
            T = Pop(S);//弹出堆栈
            printf("%5d",T->Data);//输出节点
            T = T->Right;//向弹出节点转向其有节点做一样操作
        }
    }
}

后序遍历

遍历过程：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根节点

例如：下图的遍历结果是

DEFBHGICA

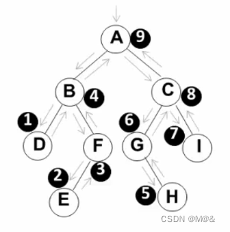
编码实现

1.利用函数递归实现

void PostOrderTraversal(BinTree BT){
      if(BT){
        PostOrderTraversal(BT->Left);
        PostOrderTraversal(BT->Right);
        printf("%5d",T->Data);//输出节点
      }
}

2.非递归函数实现，例如堆栈

此处引用其他博主的方法：

https://blog.csdn.net/Dreamluna/article/details/82780130