对于RSA非对称加密方式的理解
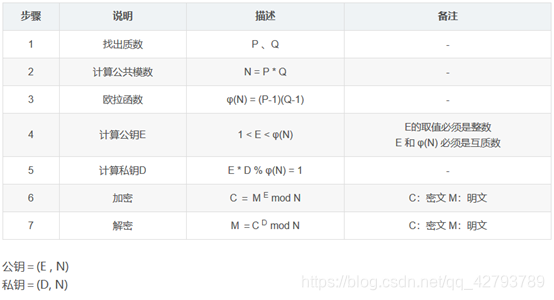
RSA加密原理:
通过非对称的公钥私钥体系,可以实现发送方A用私钥(E,N)对明文M1加密,得到密文C1,所有拥有发送方A公钥的人都可以解读密文C1。
而接收方B可以在不知道发送方A私钥的情况下,使用发送方公钥(D,N)对密文C1解密,得到明文M1。
上述过程通常用于数字签名过程(即A同时对B发送明文M1与密文C1),用于向接收方B证实发送方A的身份。
但是,当接收方B回复发送方A消息时,使用A的公钥对明文M2加密,得到密文C2,并发送给A,只有拥有私钥的A可以解读消息,从而实现通信加密。
此加密方式的最大好处为:
1.发送方和接收方使用两套不同的秘钥,加强了对密码的保护性。
2.尽管发送方A的公钥(D,N)是公开的,但是由于N很大,难以分解得到P、Q,因而无法由N得到私钥(E,N),而E从理论上无法由D推出,保障了RSA算法安全性。
数字签名的重要性:
和其它加密过程一样,对RSA来说分配公钥的过程是非常重要的。分配公钥的过程必须能够抵挡中间人攻击。假设Eve交给Bob一个公钥,并使Bob相信这是Alice的公钥,并且她可以截下Alice和Bob之间的信息传递,那么她可以将她自己的公钥传给Bob,Bob以为这是Alice的公钥。Eve可以将所有Bob传递给Alice的消息截下来,将这个消息用她自己的密钥解密,读这个消息,然后将这个消息再用Alice的公钥加密后传给Alice。理论上Alice和Bob都不会发现Eve在偷听他们的消息。今天人们一般用数字认证来防止这样的攻击。
RSA算法的破解途径:
1.数算法的不可知性:
此外寻找质数的算法不能给攻击者任何信息,这些质数P、Q是怎样找到的,尤其产生随机数的软件必须非常好。要求是随机和不可预测。这两个要求并不相同。一个随机过程可能可以产生一个不相关的数的系列,但假如有人能够预测出(或部分地预测出)这个系列的话,那么它就已经不可靠了。比如有一些非常好的随机数算法,但它们都已经被发表,因此它们不能被使用,因为假如一个攻击者可以猜出p和q一半的位的话,那么他们就已经可以轻而易举地推算出另一半。必须保证产生质数P、Q的随机数算法的机密性。
2.大数分解
RSA算法基于大数N无法被轻易分解得到两个质数,一旦N可以被轻易分解,RSA算法安全性无法得到保障。
1999年,RSA-155 (512 bits)被成功分解,花了五个月时间(约8000 MIPS年)和224 CPU hours在一台有3.2G中央内存的Cray C916计算机上完成。
2009年12月12日,编号为RSA-768(768 bits, 232 digits)数也被成功分解。这一事件威胁了现通行的1024-bit密钥的安全性,普遍认为用户应尽快升级到2048-bit或以上。
3.秀尔算法
量子计算里的秀尔算法能使穷举的效率大大的提高。由于RSA算法是基于大数分解(无法抵抗穷举攻击),因此在未来量子计算能对RSA算法构成较大的威胁。一个拥有N量子比特的量子计算机,每次可进行2^N次运算,理论上讲,密钥为1024位长的RSA算法,用一台512量子比特位的量子计算机在1秒内即可破解。