第一章 行列式
1.1 克拉默法则
举例:
对于三元线性方程组
{
a
11
x
1
+
a
12
x
2
+
a
13
x
3
=
b
1
a
21
x
1
+
a
22
x
2
+
a
23
x
3
=
b
2
a
31
x
1
+
a
32
x
2
+
a
33
x
3
=
b
3
(1)
\begin{cases} a_{11}x_{1}+a_{12}x_2+a_{13}x_3=b_1\\ a_{21}x_1+a_{22}x_2+a_{23}x_3=b_2\\ a_{31}x_1+a_{32}x_2+a_{33}x_3=b_3 \end{cases} \tag{1}
⎩
⎨
⎧
a
11
x
1
+
a
12
x
2
+
a
13
x
3
=
b
1
a
21
x
1
+
a
22
x
2
+
a
23
x
3
=
b
2
a
31
x
1
+
a
32
x
2
+
a
33
x
3
=
b
3
(
1
)
其中,
x
j
(
j
=
1
,
2
,
3
)
x_j(j=1,2,3)
x
j
(
j
=
1
,
2
,
3
)
表示未知量,
a
i
j
(
i
=
1
,
2
,
3
;
j
=
1
,
2
,
3
)
a_{ij}(i=1,2,3;j=1,2,3)
a
ij
(
i
=
1
,
2
,
3
;
j
=
1
,
2
,
3
)
表示未知量的系数,
b
i
(
i
=
1
,
2
,
3
)
b_i(i=1,2,3)
b
i
(
i
=
1
,
2
,
3
)
表示常数项。若采用代入消元法从式(1)中消去
x
2
,
x
3
x_2,x_3
x
2
,
x
3
,可以得到
x
1
x_1
x
1
,计算过程跟二元线性方程组类似。
(
a
11
a
22
a
33
+
a
11
a
23
a
31
+
a
13
a
21
a
32
−
a
11
a
23
a
32
−
a
12
a
21
a
33
−
a
13
a
22
a
31
)
x
1
=
b
1
a
22
a
33
+
b
2
a
13
a
32
+
b
3
a
12
a
23
−
b
1
a
23
a
32
−
b
2
a
12
a
33
−
b
3
a
13
a
22
(2)
(a_{11}a_{22}a_{33}+a_{11}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31})x_1\\ =b_1a_{22}a_{33}+b_2a_{13}a_{32}+b_3a_{12}a_{23}-b_1a_{23}a_{32}-b_2a_{12}a_{33}-b_3a_{13}a_{22} \tag{2}
(
a
11
a
22
a
33
+
a
11
a
23
a
31
+
a
13
a
21
a
32
−
a
11
a
23
a
32
−
a
12
a
21
a
33
−
a
13
a
22
a
31
)
x
1
=
b
1
a
22
a
33
+
b
2
a
13
a
32
+
b
3
a
12
a
23
−
b
1
a
23
a
32
−
b
2
a
12
a
33
−
b
3
a
13
a
22
(
2
)
同理可以得出仅含有
x
2
,
x
3
x_2,x_3
x
2
,
x
3
的等式,可自行写出。
若把式子(2)中的
x
1
x_1
x
1
的系数用D表示,即:
D
=
∣
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
∣
=
a
11
a
22
a
33
+
a
11
a
23
a
31
+
a
13
a
21
a
32
−
a
11
a
23
a
32
−
a
12
a
21
a
33
−
a
13
a
22
a
31
(3)
D=\left|\begin {array}{c} a_{11} &a_{12} &a_{13} \\ a_{21} &a_{22} &a_{23} \\ a_{31} &a_{32} &a_{33} \\ \end{array}\tag{3}\right|=a_{11}a_{22}a_{33}+a_{11}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}-a_{13}a_{22}a_{31}
D
=
a
11
a
21
a
31
a
12
a
22
a
32
a
13
a
23
a
33
=
a
11
a
22
a
33
+
a
11
a
23
a
31
+
a
13
a
21
a
32
−
a
11
a
23
a
32
−
a
12
a
21
a
33
−
a
13
a
22
a
31
(
3
)

则称式(3)中的D为三元线性方程组(1)的系数行列式,根据三阶行列式的定义,有:
D
=
∣
b
1
a
12
a
13
b
2
a
22
a
23
b
3
a
32
a
33
∣
=
b
1
a
22
a
33
+
a
12
a
23
b
3
+
a
13
b
2
a
32
−
b
1
a
23
a
32
−
a
12
b
2
a
33
−
a
13
a
22
b
3
(4)
D=\left|\begin {array}{c} b_1&a_{12} &a_{13} \\ b_2 &a_{22} &a_{23} \\ b_3 &a_{32} &a_{33} \\ \end{array}\tag{4}\right|=b_1a_{22}a_{33}+a_{12}a_{23}b_3+a_{13}b_2a_{32}-b_1a_{23}a_{32}-a_{12}b_2a_{33}-a_{13}a_{22}b_3
D
=
b
1
b
2
b
3
a
12
a
22
a
32
a
13
a
23
a
33
=
b
1
a
22
a
33
+
a
12
a
23
b
3
+
a
13
b
2
a
32
−
b
1
a
23
a
32
−
a
12
b
2
a
33
−
a
13
a
22
b
3
(
4
)
同理,可得:
D
2
=
∣
a
11
b
1
a
13
a
21
b
2
a
23
a
31
b
3
a
33
∣
,
D
3
=
∣
a
11
a
12
b
1
a
21
a
22
b
2
a
31
a
32
b
3
∣
D_2=\left|\begin{array}{c} a_{11}&b_1&a_{13}\\ a_{21}&b_2&a_{23}\\ a_{31}&b_3&a_{33} \end{array}\right| ,\ D_3=\left|\begin{array}{c} a_{11}&a_{12}&b_1\\ a_{21}&a_{22}&b_2\\ a_{31}&a_{32}&b_3 \end{array}\right|
D
2
=
a
11
a
21
a
31
b
1
b
2
b
3
a
13
a
23
a
33
,
D
3
=
a
11
a
21
a
31
a
12
a
22
a
32
b
1
b
2
b
3
若系数行列式
D
≠
0
,
D\neq0,
D
=
0
,
则三元线性方程组(1)的唯一解为:
x
1
=
D
1
D
,
x
2
=
D
2
D
,
x
3
=
D
3
D
x_1=\frac{D_1}{D}, x_2=\frac{D_2}{D},x_3=\frac{D_3}{D}
x
1
=
D
D
1
,
x
2
=
D
D
2
,
x
3
=
D
D
3
这里的
D
1
,
D
2
,
D
3
D_1,D_2,D_3
D
1
,
D
2
,
D
3
分别是D中的第一、二、三列元素换成
b
1
,
b
2
,
b
3
b_1,b_2,b_3
b
1
,
b
2
,
b
3
而得到的。
上述用三阶行列式解三元线性方程组的方法就称为三元线性方程组的
克拉默法则
。
1.2 n阶行列式
1.3 特殊行列式
(1)上三角行列式
主对角线左下方元素全为零的行列式称为
上三角行列式
。上三角行列式的值等于主对角线元素的乘积。
∣
a
11
a
12
…
a
1
n
0
a
22
…
a
2
n
⋮
⋮
⋮
0
0
…
a
n
n
∣
=
a
11
a
22
…
a
n
n
\left|\begin{array}{c} a_{11}&a_{12}&\dots&a_{1n}\\ 0&a_{22}&\dots&a_{2n}\\ \vdots&\vdots& &\vdots\\ 0&0&\dots&a_{nn} \end{array}\right|=a_{11}a_{22}\dots a_{nn}
a
11
0
⋮
0
a
12
a
22
⋮
0
…
…
…
a
1
n
a
2
n
⋮
a
nn
=
a
11
a
22
…
a
nn
(2)下三角行列式
主对角右上方元素全为零的行列式称为
下三角行列式
。下三角行列式的值也和上三角的一样,为主对角线元素的乘积。
∣
a
11
0
…
0
a
21
a
22
…
0
⋮
⋮
⋮
a
n
1
a
n
2
…
a
n
n
∣
=
a
11
a
22
…
a
n
n
\left|\begin{array}{c} a_{11}&0&\dots&0\\ a_{21}&a_{22}&\dots&0\\ \vdots&\vdots& &\vdots\\ a_{n1}&a_{n2}&\dots&a_{nn} \end{array}\right|=a_{11}a_{22}\dots a_{nn}
a
11
a
21
⋮
a
n
1
0
a
22
⋮
a
n
2
…
…
…
0
0
⋮
a
nn
=
a
11
a
22
…
a
nn
(3)对角行列式
主对角元素以外元素全为零的行列式称为
对角行列式
。对角行列式既是上三角行列式,又是下三角行列式,其值等于主对角线元素的成绩。
∣
a
11
0
…
0
0
a
22
…
0
⋮
⋮
⋮
0
0
…
a
n
n
∣
=
a
11
a
22
…
a
n
n
\left|\begin{array}{c} a_{11}&0&\dots&0\\ 0&a_{22}&\dots&0\\ \vdots&\vdots& &\vdots\\ 0&0&\dots&a_{nn} \end{array}\right|=a_{11}a_{22}\dots a_{nn}
a
11
0
⋮
0
0
a
22
⋮
0
…
…
…
0
0
⋮
a
nn
=
a
11
a
22
…
a
nn
1.4 行列式的性质和推论
性质1:行列式与它的转置行列式相等,即
D
=
D
T
D=D^{T}
D
=
D
T
。

性质2:交换行列式的任意两行(列),行列式仅仅改变符号,即正的变负的,负的变正的。
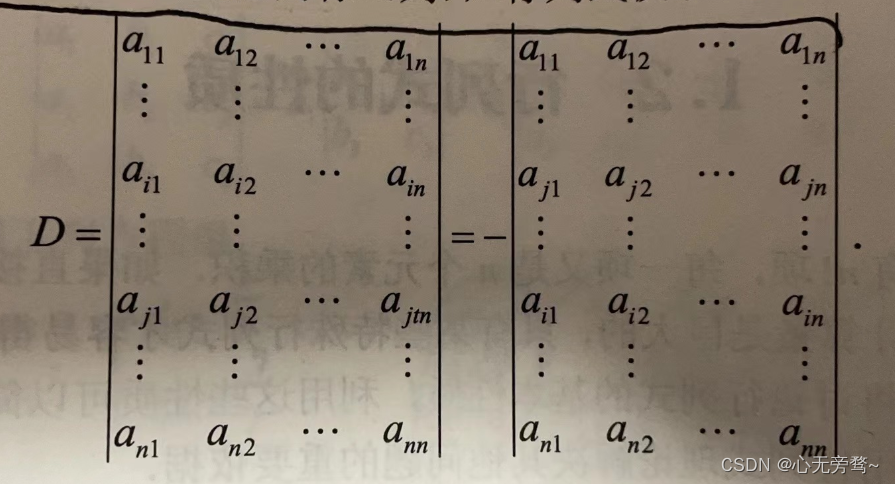
推论3:如果行列式中有两行(列)对应元素相同,则此行列式的值为0。
证明:由性质2可知,
D
=
−
D
D=-D
D
=
−
D
,则
2
D
=
0
2D=0
2
D
=
0
,故
D
=
0
D=0
D
=
0
。
性质3:如果将行列式D的某一行(列)的所有元素同乘以数k,其结果等于用数k乘以此行列式D。
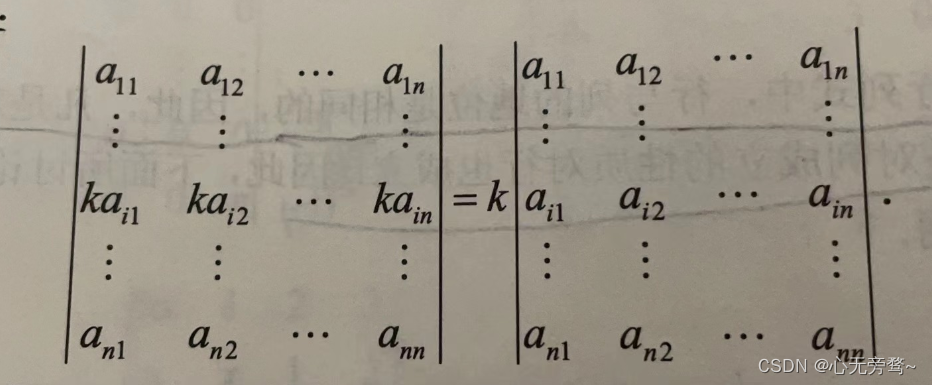
推论4:如果行列式D中的某一行(列)的所有元素都有公因子k,则可以把k提到行列式的外面。
推论5:如果行列式中有两行(列)元素对应成比例,则此行列式的值等于0。

性质4:若行列式D中的某一行(列)的元素都是两数之和,例如,第
i
i
i
行的元素是两数之和。

则D等于下列两个行列式之和:

性质5:把行列式某一行(列)的各元素都乘以同一常数k,然后加到另一行(列)的对应元素上去,行列式的值不变。

1.5 余子式和代数余子式
在n阶行列式
D
=
d
e
t
(
a
i
j
)
D=det(a_{ij})
D
=
d
e
t
(
a
ij
)
中,划去元素
a
i
j
a_{ij}
a
ij
所在的第
i
i
i
行和第
j
j
j
列后,余下的元素按照原来的位置构成
n
−
1
n-1
n
−
1
阶行列式,称为
D
D
D
中元素
a
i
j
a_{ij}
a
ij
的
余子式
,记为
M
i
j
M_{ij}
M
ij
。
a
i
j
a_{ij}
a
ij
的余子式
M
i
j
M_{ij}
M
ij
前添加符号
(
−
1
)
i
+
j
(-1)^{i+j}
(
−
1
)
i
+
j
,称为元素
a
i
j
a_{ij}
a
ij
的
代数余子式
,记作
A
i
j
A_{ij}
A
ij
,即:
A
i
j
=
(
−
1
)
i
+
j
M
i
j
A_{ij}=(-1)^{i+j}M_{ij}
A
ij
=
(
−
1
)
i
+
j
M
ij
按照余子式、代数余子式的定义,三阶行列式的展开式可以改写为:
D
=
∣
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
∣
=
a
11
∣
a
22
a
23
a
32
a
33
∣
−
a
12
∣
a
21
a
23
a
31
a
33
∣
+
a
13
∣
a
21
a
22
a
31
a
32
∣
=
a
11
M
11
−
a
12
M
12
+
a
13
M
13
=
(
−
1
)
1
+
1
a
11
A
11
−
(
−
1
)
1
+
2
a
12
A
12
+
(
−
1
)
1
+
3
a
13
A
13
D=\left|\begin{array}{c} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33} \end{array}\right|=a_{11}\left|\begin{array}{c}a_{22}&a_{23}\\ a_{32}&a_{33}\end{array}\right|-a_{12}\left|\begin{array}{c}a_{21}&a_{23}\\ a_{31}&a_{33}\end{array}\right|+a_{13}\left|\begin{array}{c}a_{21}&a_{22}\\ a_{31}&a_{32}\end{array}\right|\\ =a_{11}M_{11}-a_{12}M_{12}+a_{13}M_{13}=(-1)^{1+1}a_{11}A_{11}-(-1)^{1+2}a_{12}A_{12}+(-1)^{1+3}a_{13}A_{13}
D
=
a
11
a
21
a
31
a
12
a
22
a
32
a
13
a
23
a
33
=
a
11
a
22
a
32
a
23
a
33
−
a
12
a
21
a
31
a
23
a
33
+
a
13
a
21
a
31
a
22
a
32
=
a
11
M
11
−
a
12
M
12
+
a
13
M
13
=
(
−
1
)
1
+
1
a
11
A
11
−
(
−
1
)
1
+
2
a
12
A
12
+
(
−
1
)
1
+
3
a
13
A
13
定理:n阶行列式
D
=
d
e
t
(
a
i
j
)
D=det(a_{ij})
D
=
d
e
t
(
a
ij
)
等于它的任意一行(列)的各元素与其对应的
代数余子式的乘积之和**,即:**
D
=
a
i
1
A
i
1
+
a
i
2
A
i
2
+
⋯
+
a
i
n
A
i
n
(
i
=
1
,
2
,
…
,
n
)
D=a_{i1}A_{i1}+a_{i2}A_{i2}+\dots+a_{in}A_{in}(i=1,2,\dots,n)
D
=
a
i
1
A
i
1
+
a
i
2
A
i
2
+
⋯
+
a
in
A
in
(
i
=
1
,
2
,
…
,
n
)
推论6:行列式某一行(列)的元素与另一行(列)对应元素的代数余子式的乘积之和等于0,即:


1.6 范德蒙德行列式

