一. 基础知识
在优化的过程中,只有凸函数局部最优解是全局最优解,因而能够通过梯度下降法找到全局最优解。
二阶可微函数为凸函数的充要条件为
Hessian
矩阵半正定。
均方差损失函数(
MSE
),用于线性回归中。
由于
sigmoid
等非线性激活函数的存在,使得均方差损失函数在
logistic
回归和
neural network
中,不是凸函数,不能通过梯度下降的方法找到局部最优解,进而得到全局最优解。
交叉熵损失函数,是极大似然估计的直接产物。
在分类问题中,作为
logistic
回归和
neural network
的的损失函数。
在
logistic
回归中是权重w的凸函数,在
neural network
中不是凸函数。
信息量,一个事件所能提供信息的多少。
信息量的大小跟事情
不确定性的变化
有关。
1>不确定性的变化与什么有关?
=>与事情的可能结果的数量有关,与概率有关。
2>如何衡量不确定性的变化的大小?
=>
一个事件的信息量就是这个事件发生的概率的负对数
。
I
(
x
j
)
=
−
ln
p
(
x
j
)
I(x_{j}) = – \ln_{}{p(x_{j})}
I
(
x
j
)
=
−
ln
p
(
x
j
)
可以看出当
p
(
x
i
)
=
1
p(x_{i})=1
p
(
x
i
)
=
1
时,即事件的不确定完全消失时,熵为零。
一个不太可能发生的事件发生了,要比一个非常可能发生的事件,提供更多的信息。
信息熵,代表随机变量或整个系统的不确定性。
对整个概率分布进行量化,是跟所有可能性有关系的。每个可能事件的发生都有个概率,信息熵就是平均而言发生一个事件可以得到的信息量的大小。
数学上,
信息熵是信息量的期望
。
H
(
X
)
=
E
(
I
(
x
i
)
)
=
−
∑
i
=
1
n
p
i
log
p
i
H(X)=E(I(x_{i}))=-\sum_{i=1}^{n}p_{i} \log_{}{p_{i}}
H
(
X
)
=
E
(
I
(
x
i
))
=
−
∑
i
=
1
n
p
i
lo
g
p
i
,其中X为所有可能的事件,
p
i
p_{i}
p
i
为事件
x
i
x_{i}
x
i
发生的概率。
加权熵,通多权重来体现各个事件的重要程度。
H
w
(
X
)
=
−
∑
i
=
1
n
w
i
p
i
log
p
i
H_{w}(X)=-\sum_{i=1}^{n} w_{i} p_{i} \log_{}{p_{i}}
H
w
(
X
)
=
−
∑
i
=
1
n
w
i
p
i
lo
g
p
i
交叉熵,用来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
H
(
p
,
q
)
=
−
∑
j
=
1
n
p
(
x
j
)
ln
q
(
x
j
)
H(p, q)=-\sum_{j=1}^{n} p(x_{j})\ln_{}{q(x_{j})}
H
(
p
,
q
)
=
−
∑
j
=
1
n
p
(
x
j
)
ln
q
(
x
j
)
交叉熵越低,由算法所产生的策略越接近最优策略。
当
p
k
=
q
k
p_{k}=q_{k}
p
k
=
q
k
,交叉熵=信息熵,得到最低的交叉熵。即表明了使用真实分布所计算出来对的信息熵。
相对熵,用来衡量两个取值为正的函数或概率分布之间的差异。
相对熵=交叉熵(某个策略)- 信息熵(根据真实分布计算的)
D
K
L
=
∑
j
=
1
n
p
j
ln
p
j
q
j
=
∑
j
=
1
n
p
j
ln
p
j
−
∑
j
=
1
n
p
j
ln
q
j
=
−
H
(
p
(
x
)
)
+
H
(
p
,
q
)
D_{KL} = \sum_{j=1}^{n} p_{j}\ln_{}{\frac{p_{j}}{q_{j}}} = \sum_{j=1}^{n}p_{j}\ln_{}{p_{j}} – \sum_{j=1}^{n}p_{j}\ln_{}{q_{j}} = -H(p(x))+H(p,q)
D
K
L
=
∑
j
=
1
n
p
j
ln
q
j
p
j
=
∑
j
=
1
n
p
j
ln
p
j
−
∑
j
=
1
n
p
j
ln
q
j
=
−
H
(
p
(
x
))
+
H
(
p
,
q
)
二、回归问题
计算预测值与实际值之间的误差来衡量模型的优劣。
最常用的是
MSE
:
M
S
E
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
MSE = \frac{1}{n} \sum_{i=1}^{n} (y_{i} – \hat{y}_{i})^{2}
MSE
=
n
1
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
缺点:在异常点位置会施以较大的惩罚,所以若存在较多的异常点(或重尾数据),此时
MAE
效果更好。
不过,
MAE
在
y
i
−
y
^
i
=
0
y_{i} – \hat{y}_{i}=0
y
i
−
y
^
i
=
0
处不连续可导,所以不容易优化。
Huber
综合二者,是一种使用鲁棒性回归的损失函数,相比较
MSE
,对异常值不敏感。
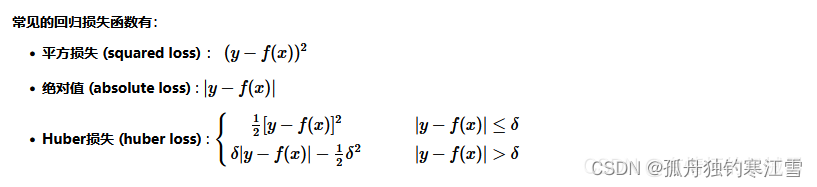
二. 分类问题
回归损失:nn.L1Loss() 计算实际值与预测值之间的绝对差之和的平均值
nn.MSELoss() 计算实际值和预测值之间的平方差的平均值
nn.SmoothL1Loss() 以上二者的结合
分类损失
nn.NLLLoss() 负对数似然损失 nn.NLLLoss()+nn.LogSoftmax() = nn.CrossEntropyLoss()
nn.CrossEntropyLoss() 交叉熵损失函数
import torch
import torch.nn as nn
preds = torch.tensor([[1.5,2.5,3.0]]) # 模仿经过模型之后的输出结果
target = torch.tensor([1]) # 真实标签
cross_entropy_loss = torch.nn.CrossEntropyLoss()
log_softmax = torch.nn.LogSoftmax(dim=1)
nllloss = torch.nn.NLLLoss()
cs_loss = cross_entropy_loss(preds,target)
nls_loss = nllloss(log_softmax(preds),target)
print(f’交叉熵损失函数为:{cs_loss}\n先经过log_softmax再经过nll损失函数为:{nls_loss}’)
