#十进制数转换为二进制数
十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1、十进制整数转换为二进制整数
十进制整数转换为二进制整数采用”除2取余,逆序排列”法。具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为零时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
【例1 】 把 十进制173 转换为二进制数。
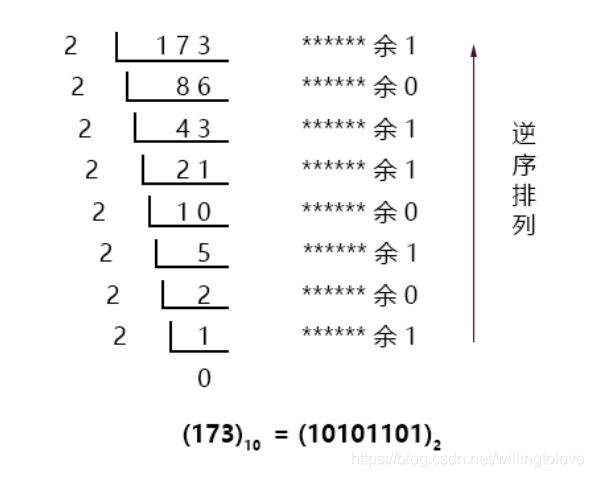
2、十进制小数转换为二进制小数
十进制小数转换成二进制小数采用”乘2取整,顺序排列”法。具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数 部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
【例2】把十进制小数 0.8125转换为二进制小数。

【例3】将十进制数173.8125转为二进制数。
把整数部分和小数部分合并得:
(173.8125)
10
=(10101101.1101)
2
#浮点类型数据的存储
无论是单精度还是双精度在存储中都分为三个部分:
符号位(Sign) : 0代表正,1代表为负
指数位(Exponent):用于存储科学计数法中的指数数据,并且采用移位存储
尾数部分(Mantissa):尾数部分
其中单精度float类型数据的存储方式如下图所示:
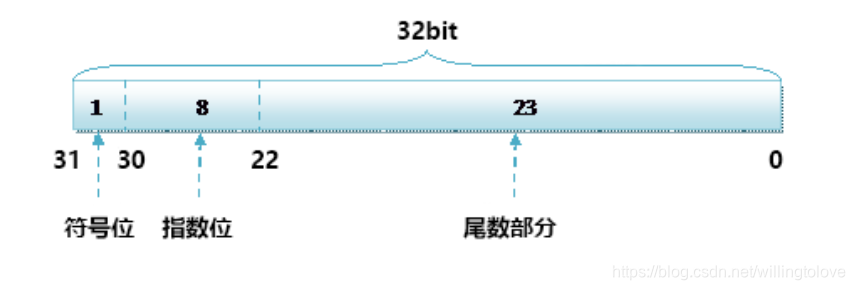
而双精度double的存储方式为:
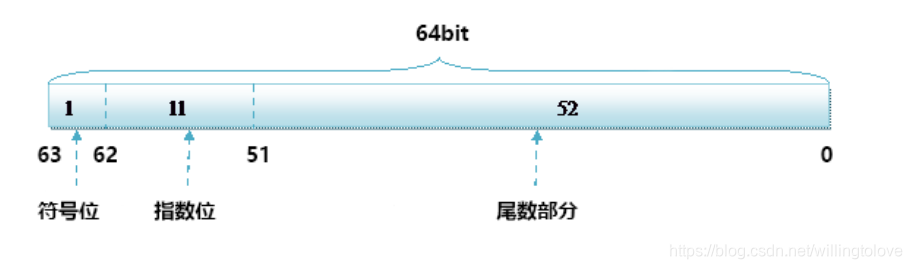
比如8.25用十进制的科学计数法表示为:8.2510º,而120.5可以表示为:1.20510²。而计算机根本不认识十进制的数据,他只认识0,1。所以在计算机存储中,首先要将上面的数更改为二进制的科学计数法表示。8.25用二进制表示可表示为1000.01。120.5用二进制表示为:1111000.1。
用二进制的科学计数法表示1000. 01可表示为1. 00001×2^3, 而1110110. 1则可表示为1. 1101101×2^6, 任何一个数的科学计数法都可表示为1. xxx×2^n;因此尾数部分就可表示为xxx,反正第一位都是1嘛,干嘛还要表示呀! ?故可将小数点前面的1省略,故23bit的尾数部分,可以表达的精度却变成了24bit,道理就是在这里;那24bit能精确到小数点后的几位呢?我们知道,9的二进制
表示为1001,所以4bit能精确十进制中的1位小数点,24bit 就能使float能精确到小数点后6位;另算上可以估读最后一位,故有效位数为7位。
而对于指数部分,因为指数可正可负,8位的指数位能表示的指数范围就应该为-127至128了,所以指数部分的存储采用移位存储,存储的数据为原数据加127,下面就看看8.25和120.5在内存中真正的存储方式。
首先看下8.25,用二进制的科学计数法表示为: 1. 00001×2^3。按照上面的存储方式,符号位为0,表示为正:指数位为3+127=130 (二进制值10000010);尾数部分为00001,故8.25的存储方式如下图所示:
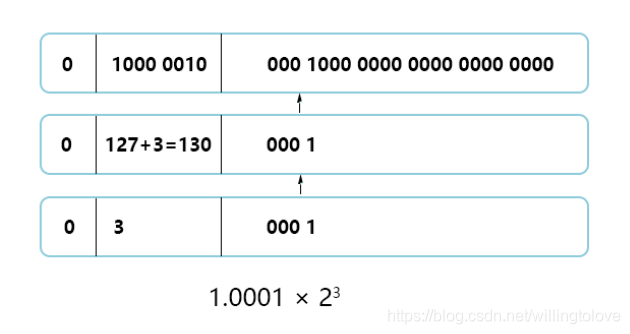
而单精度浮点数120.5的存储方式如下图所示:

#其他总结
1、关于浮点数的精度与范围:
- .浮点数表示的主要目标是: 用尽量短的字长,实现尽可能大的表数范围和尽可能高的表数精度。
- 尾数的位数越多,有效精度越高;
- 阶码的位数越多,范围越大。
- 设计时,如果字长一定,则需要在精度和范围之间作一权衡。
2、关于浮点数的分布:与整数的均匀分布相比,浮点数有以下特点
- 越靠近零点处,数的分布越密,能够表示的精度越高,
- 越远离零点处,数的分布越稀疏,能够表示的范围越大。
#参考