硬币收集问题描述如下:在nxm格木板上放一些硬币,在左上方的机器人要收集尽可能多的硬币到右下方,机器人可以向右或向下移动。计算出机器人一共能收集到的最多数量的硬币,并求出其运动轨迹?
算法分析:
令F(i,j)为机器人移动到(i,j)时收集到的最大硬币数
F(i,j)=max{F(i-1,j),F(i,j-1)}+cij ,1<=i<=n,1<=j<=m
//要不是从上移动过来,要不是从左移动到达当前位置,取较大值!
F(0,j)=0, 1<=j<=m; F(i,0)=0, 1<=i<=n,
//在棋盘外设置第0行第零列,并归零。
若(i,j)格中有硬币,则cij为1,否则为0
以下举一个实例分析:
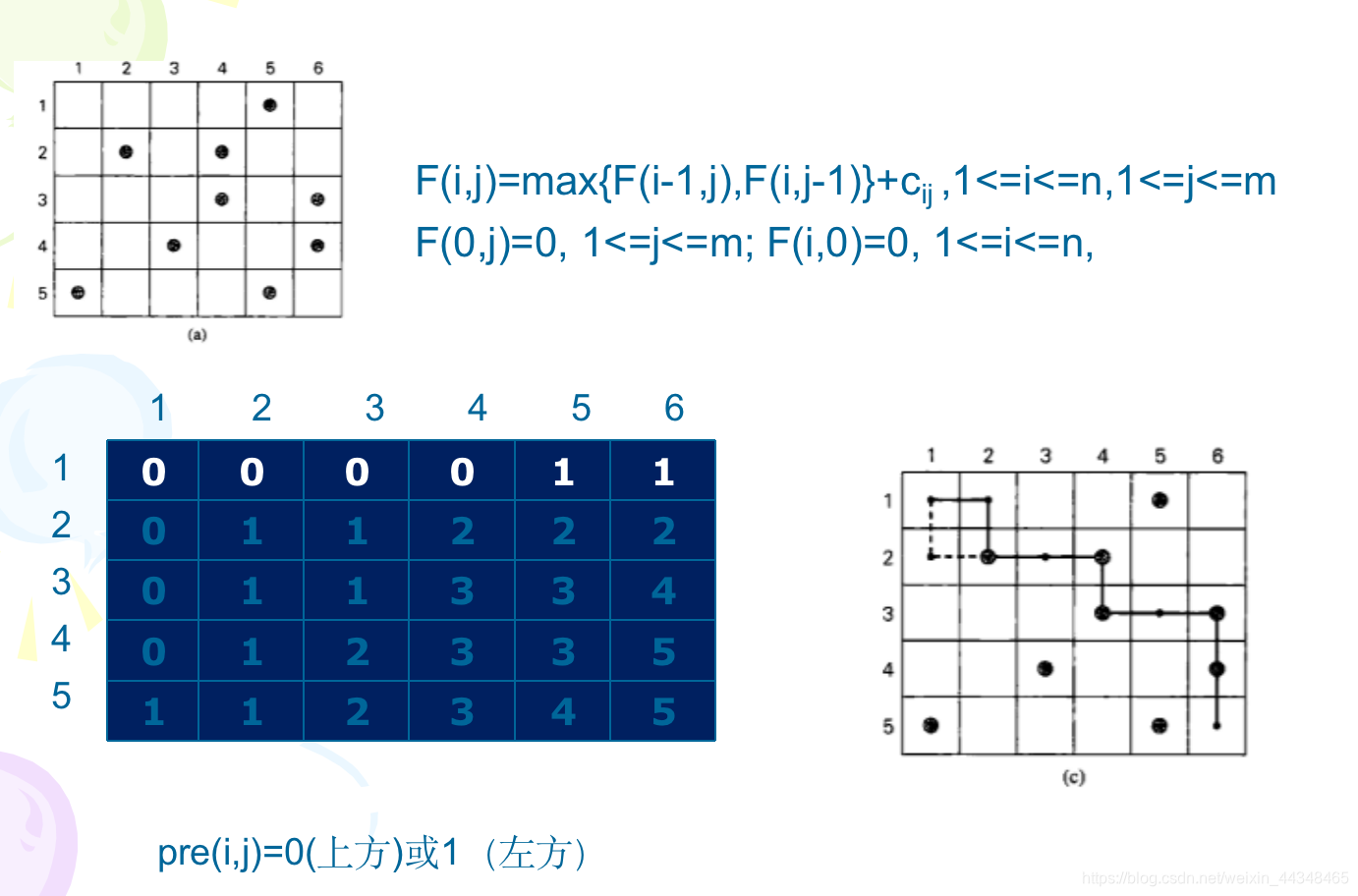
计算最多硬币数关键代码:
void FindMax()
{
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
F[i][j]=Max(F[i-1][j],F[i][j-1])+arr[i][j];
}
}
printf("\n最多搜集 %d 个硬币。\n",F[m][n]);
}
完整代码实现:
#include <iostream>
#define MAX 10
int m,n; //方格的行和列
int arr[MAX][MAX]; //储存原始方格元素
int F[MAX][MAX]; //保存收集到的最大硬币数
int H[MAX][MAX];//进行回溯操作时,保存路线坐标
void HuiSu(); //函数声明
void FindMax();
int Max(int a,int b);
int main()
{
printf("请输入方格的行数和列数:(空格隔开)\n"); //行列中数组的下标0都不用
scanf("%d%d",&m,&n);
for(int i=0;i<=m;i++) //第0列全部置0
{arr[i][0]=0;}
for(int j=0;j<=n;j++)//第0行全部置0
{arr[0][j]=0;}
for(int i=1;i<=m;i++)
{
printf("请输入第%d行的%d个数:(只能出现0或1)\n",i,n);
for(int j=1;j<=n;j++)
{
scanf("%d",&arr[i][j]);
}
}
printf("创建的%d行%d列的木板如下:\n ",m,n);
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
printf("%d ",arr[i][j]);
}
printf("\n ");
}
FindMax();
printf("收集的路线为:\n");
HuiSu();
return 0;
}
int Max(int a,int b) //求较大值函数
{
return a>=b? a:b;
}
void FindMax()
{
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
F[i][j]=Max(F[i-1][j],F[i][j-1])+arr[i][j];
}
}
printf("\n最多搜集 %d 个硬币。\n",F[m][n]);
}
void HuiSu()//回溯,查找到达当前位置,是从左边还是上面来的。
{
int a=m;
int b=n;
H[1][1]=1; //起点和终点都为必经过的点
H[m][n]=1; //
while(a>=1&&b>=1)
{
if(F[a-1][b]>=F[a][b-1])
{
H[a-1][b]=1;
a--; //横坐标减一,说明从左过来的
}
else
{
H[a][b-1]=1;
b--; //纵坐标减一,说明从上过来的
}
}
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
if(H[i][j]==1)
{
if(i==m&&j==n)
printf("(%d,%d)\n",m,n);
else
printf("(%d,%d)-->",i,j);
}
}
}
运行效果如下:
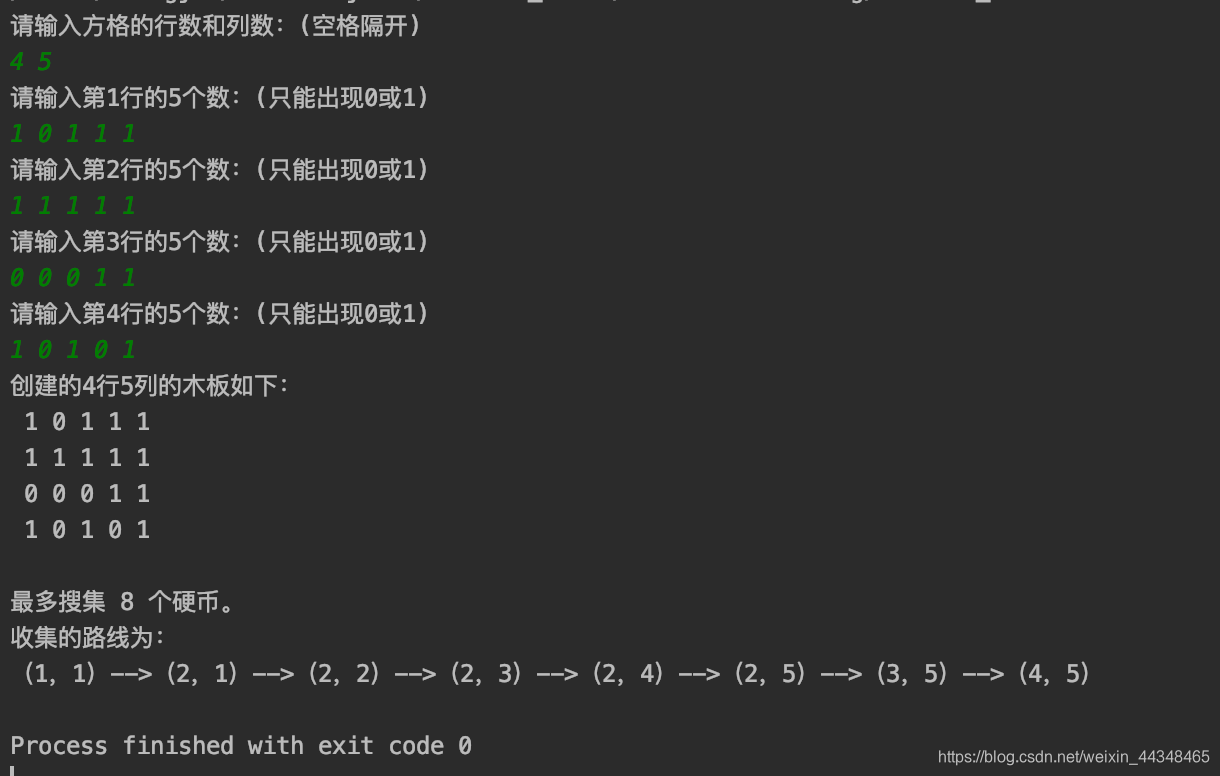
bingo!这个题就搞定了。
版权声明:本文为weixin_44348465原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。