一:LeetCode977.有序数组的平方
1:题目描述(
977.有序数组的平方
)
给你一个按
非递减顺序
排序的整数数组
nums
,返回
每个数字的平方
组成的新数组,要求也按
非递减顺序
排序。

2:解题思路
解法一:暴力解法:
先遍历数组,对元素进行平方,再对数组进行排序
class Solution:
def sortedSquares(self, nums):
# 暴力解法:先进行平方,再进行排序
for i in range(len(nums)):
nums[i] = nums[i] * nums[i]
nums.sort()
return nums
解法二:使用双指针
定义两个指针,分别指向数组的一头一尾;
定义一个新的数组,长度与原始数组保持一致,元素的初始值均置为0;
然后对比两个指针所指向值的平方后的大小,将较大平方值,从后往前替换掉新数组的值。
代码展示:
class Solution:
def sortedSquares(self, nums):
# 双指针解法
# 定义两个指针,分别指向数组的一头一尾,在定义一个新数组,比较两个指针对应的值,将较大的值从新数组的后面往前进行替换
n = len(nums)
res = [0] * n
left, right, size = 0, n-1, n-1 # size代表数组res当前指向的位置
while left <= right:
if nums[left]*nums[left] >= nums[right]*nums[right]:
res[size] = nums[left]*nums[left]
left += 1
size -= 1
else:
res[size] = nums[right]*nums[right]
right -= 1
size -= 1
return res
二、LeetCode209.长度最小的子数组
1:题目描述(
209.长度最小的子数组
)
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。

2:解题思路
首先定义一个无穷大的数res_len,一个求和的变量Sum以及子数组的起始位置index;
遍历数组,将当前遍历的值与Sum进行求和,
判断求和后的结果是否大于等于目标值target,满足条件,获取满足条件的子数组长度,然后求res_len和满足条件的子数组的长度的最小值,找到满足条件的子数组后,我们需要将子数组起始位置的值从Sum中减去,并将子数组的起始位置index向右移动一位,进行循环判断是否满足条件,不满足条件了,继续遍历数组,直到数组遍历结束。
代码展示:
class Solution:
def minSubArrayLen(self, target, nums):
# 初始化满足条件的长度,初始化为最大值
res = float("inf")
# 初始化满足条件的元素之和,初始化为0
Sum = 0
# 初始化起始位置,初始化为第一个元素的下标
index = 0
# 遍历数组
for i in range(len(nums)):
# 求和,与当前遍历的值
Sum += nums[i]
# 判断当前元素之和,是否大于等于目标值target
while Sum>= target:
# 当前元素之和大于等于目标值,更新res的值,取当前res和当前遍历到的元素下标与index之间的长度中的最小值
res = min(res, i-index+1)
# 减去起始位置的元素
Sum -= nums[index]
# 向右移动起始位置
index += 1
return 0 if res==float("inf") else res
三、LeetCode59.螺旋矩阵II
1:题目描述(
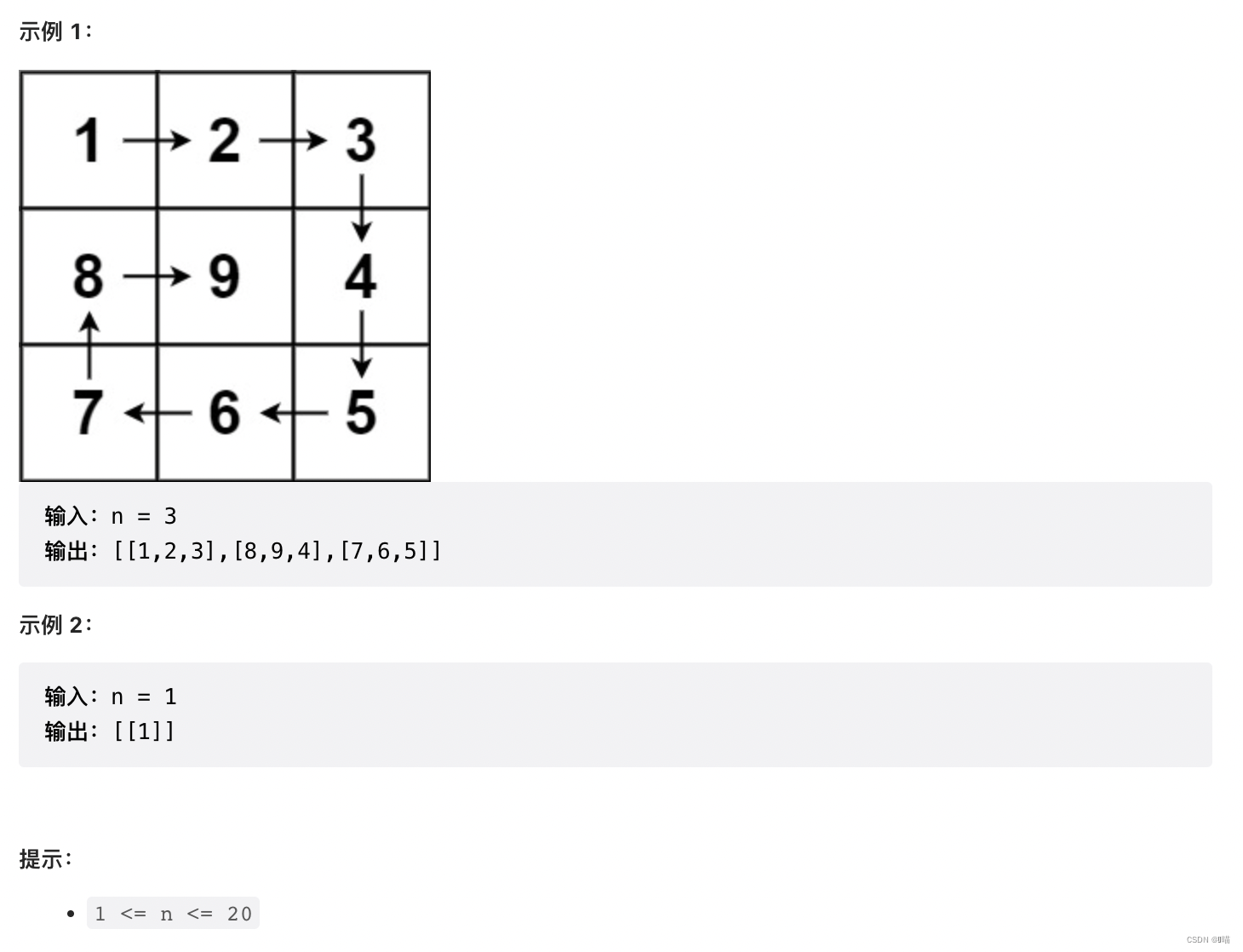
59.螺旋矩阵II
)
给你一个正整数
n
,生成一个包含
1
到
n2
所有元素,且元素按顺时针顺序螺旋排列的
n x n
正方形矩阵
matrix
。
2:解题思路
先偷个懒,明天补上。
今日总结:
首先来说第一题:977.有序数组的平方,受昨天27.移除元素的影响,一直在考虑要在同一个数组中实现,不增加额外的数组空间,导致想了半天怎么也没想通;
第二题呢:思路一下子就出来了,但是在代码实现上还是有点小问题;
第三题,完全就是没思路了,还是瞄了一眼以前写的代码,才想起来。
整体感觉就是以前写了的,也理解了的,但是自己现在再写,就是一脸懵逼,无从下手的状态,不知道是不是没理解透彻,然后自己认为自己理解透彻了。因为工作的原因,今天暂时先到这儿了,明天把该补的在补上。