一、质数
1.判断一个数n是不是质数,只需从2开始一直遍历到根号n即可,因为如果n能被一个小于根号n的数整除,那么必定存在一个大于根号n的数。
筛质数:
1.暴力做法:从2遍历到n,不管遍历到的是质数还是合数,都把他的倍数筛掉(Onlogn)。
2.埃式筛法:仅用遍历到的质数把后面的所有合数筛掉(Onloglogn)
3.线性筛:用最小质因子去筛合数(质数从小到大遍历,筛掉i
primej,若i%primej = 0说明当前质数是i也是i
primej的最小质因子,若j再+1,则当前质数不是i*primej的最小质因子了,为了避免重复筛所以要退出循环)。循环遍历中,每筛掉一个数只用了一次,因此复杂度是On的。
二、约数
1.求约数的方法和求质数类似,比求质数多了一步判断i是否等于n/i,若不等说明在大于根号n的地方还有一个约数n/i,要把其一起加入约数序列。
2.求约数的个数:N=ans=d=pα11∗pα22∗⋯∗pαkk(α1+1)(α2+1)…(αk+1)因为任何一个约数d可以表示成pβ11∗pβ22∗⋯∗pβkk,0≤βi≤αi每一项的βi如果不同,那么约数d就不相同(算数基本定理,每个数的因式分解是唯一的)所以n的约数就跟βi的选法是一一对应的β1一共有0∼α1种选法β2一共有0∼α2种选法…βk一共有0∼αk种选法乘法原理,一共有ans个约数。约数可以表示为所有质因子的不同次幂的乘积,将每一项的质因子提取出来,统计数量加和乘起来即可。
3.约数之和:由上述可知N的所有约数之和等于 (p10+p11+…+p1c1)∗…∗(pk0+pk1+…+pkck)。而求pb+pb−1+…+1可用while (b – ) t = t * a + 1来完成。
4.最大公约数:辗转相除法(欧几里得算法)
int gcd(int a, int b){
return b ? gcd(b,a%b):a;
}
a%b可看成a – k
b,因此若d是a和b的公约数,则d也是a%b,b的公约数,而若d是b,a%b 的公约数
则 d|a-k
b+k*b = d|a,故d也是a和b的公约数。因此(a,b)的公约数集合和(b,a%b)的公约数集合相同 所以他们的最大公约数也相同 ,而辗转相除法会将两个数慢慢减小,当两个数不存在公约数(b=0时),则返回a(一个数和0的最大公约数是它本身)。
三、欧拉函数
1.对于正整数nn,欧拉函数是小于或等于nn的正整数中与nn互质的数的数目,记作φ(n).φ(1)=1
根据容斥原理,将N中所有质因子的倍数去掉,加上任意两个质因子的乘积的倍数,减去任意三个质因子的乘积的倍数…就是ϕ(N) = N×p1−1p1×p2−1p2×…×pm−1pm 展开
2.求n的质因子可用线性筛优化。
四、快速幂
又叫反复平方法,类似位运算的思想,将原来On的计算优化到Ologn。
求a的b次方,可将b拆分为2的0次方、2的1次方、2的2次方…2的log2b次方,每次取出b的二进制的最后一位数字,乘以a,后将b右移一位,将a平方。
快速幂可用于求逆元:
乘法逆元的定义
若整数 b,m 互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(modm),则称 x 为 b 的模 m 乘法逆元,记为 b
−1
(modm)。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。由费马小定理可知,当m为质数时
b ^m – 1^ ≡ 1 (mod m)拆一个b出来可得 b * b ^m – 2^ ≡ 1 (mod m),所以b
m−2
即为 b 的乘法逆元。
五、扩展欧几里得算法
裴蜀定理:对任意一对a ,b 一定存在x,y使得ax+by = gcd(a,b)
且是x和y能凑出来的最小的正整数。(a是gcd的倍数,b也是gcd的倍数,因此ax+by一定也是gcd的倍数,因此最小是gcd)
用扩展欧几里得算法求x和y:
当 b=0时 ax+by=a故而 x=1,y=0
当 b≠0 时
因为
gcd(a,b)=gcd(b,a%b)
而
bx′+(a%b)y′=gcd(b,a%b)
bx′+(a−⌊a/b⌋∗b)y′=gcd(b,a%b)
ay′+b(x′−⌊a/b⌋∗y′)=gcd(b,a%b)=gcd(a,b)
故而
x=y′,y=x′−⌊a/b⌋∗y′(y-=a/b * x)
因此可以采取递归算法 先求出下一层的x′和y′ 再利用上述公式回代即可。
扩展欧几里得算法就是在求最大公约数的过程中,把a和b的系数x和y求出。
应用: 求解一次同余方程 ax≡b(modm)
则等价于求
ax=m∗(−y)+b
ax+my=b
有解条件为 gcd(a,m)|b,然后用扩展欧几里得求解即可
特别的 当 b=1且 a与m互质时 则所求的x即为a的逆元
六、中国剩余定理
中国剩余定理:在模数两两互质的情况下,一元线性同余方程组的解为
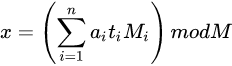
若不保证模数两两互质的一元线性同余方程组应如何求解?
对于每两个式子(我们考虑将其合并):
x≡m1(% a1)x≡m1(% a1)
x≡m2(% a2)x≡m2(% a2)
则有:
x=k1∗a1+m1x=k1∗a1+m1
x=k2∗a2+m2x=k2∗a2+m2
进一步:
k1∗a1+m1=k2∗a2+m2k1∗a1+m1=k2∗a2+m2
移项:
k1∗a1−k2∗a2=m2−m1k1∗a1−k2∗a2=m2−m1
也就是:
① k1∗a1+k2∗(−a2)=m2−m1
我们已知a1,m1,a2,m2可以用扩展欧几里得算法算出一个k′1,k′2使得:
k′1∗a1+k′2∗(−a2)=gcd(a1,−a2) 方程有解的条件是m2-m1可以被gcd(a1,-a2)整除。
我们设d=gcd(a1,−a2),y=(m2−m1)d
承接上文,我们只需让k1,k2分别扩大y倍,则可以找到一个k1,k2满足①式:
k1=k′1∗y,k2=k′2∗y
3. 找到最小正整数解
我们知道一个性质:
②k1=k1+k∗a2d
k2=k2+k∗a1d
k为任意整数,这时新的k1,k2仍满足①式。
要找一个最小的非负整数解,我们只需要让
k1=k1% abs(a2d)
k2=k2% abs(a1d)
即可找到当前最小的k1,k2的解。
由②式带入
新的x为:
x=(k1+k∗a2d)∗a1+m1
=k1∗a1+m1+k∗a2∗a1/d
=k1∗a1+m1+k∗lcm(a1,a2)(最小公倍数)
此时,将k设为k,lcm(a1,a2)设为a,k1∗a1+m1设为m,即完成了将两个线性同余方程合并为一个。以此类推,最后将所有方程合并(若有解),可得到x=ka+m,符合条件的解即m%a。
七、高斯消元
思想就是线代的利用初等行变换将矩阵变为行最简形求解。
枚举每一列c,
找到当前列绝对值最大的一行
用初等行变换 把这一行换到最上面(未确定阶梯型的行,并不是第一行)
用初等行变换 将该行的第一个数变成 1 (其余所有的数字依次跟着变化)
用初等行变换 将下面所有行的当前列的值变成 0(此时矩阵变为行阶梯形)
后从有系数的最后一行(若r<n,且一行无系数但b不为0,说明方程组无解)开始,用每行的第一列非零元素将上方的元素清零(具体操作就是上方行数小的b-=同列但行数小的元素*该行的b)
最后输出每一行的b,即为方程组的解。
求解异或线性方程组:异或操作可看成是不进位的加法,异或线性方程组可看成系数为0或1,解也为0或1的线性方程组。
八、求组合数
组合数即Cba,方法如下:
1.利用公式 Cba=Cb−1a−1+Cba−1:从a中任意挑b个数,对任意数而言可分且仅能为两种情况:①挑中了这个数,即在a-1个中挑了b-1个数,Cb-1a-1。②没挑中这个数,即在a-1个中挑了b个数,Cba−1。
时间复杂度为O(n²)边界情况:任意j为0时,Cji= 1。
2.当询问特别多而a和b的值不是很大时,可用快速幂和费马小定理求Cba,
即Cba=a!/(b!*(a-b)!),将分母用逆元表示,则公式转化为a!*infact(b!)*infact(a-b!)
则可用快速幂和费马定理求出其中的阶乘及逆元。
时间复杂度为O(a∗log(mod))
3.卢卡斯定理O(logpNplogp)
4.高精度乘法+筛质数
5.满足条件的01序列:求满足任意前缀序列中 0 的个数都不少于 1 的个数的序列。可看成从0,0走到n,n的序列中不超过对角线的序列。同时任意超过对角线的序列最后的终点都走到了n-1,n+1,因此合法的序列=C(n,2n)-C(n-1,2n)。即卡特兰数
九、容斥原理
求多个集合的并集(…至少有一个…)可以用容斥原理:
⋃
m
i=1 Si=S1+S2+…+Sm−(S1⋂S2+S1⋂S3+…+Sm−1⋂Sm)+(S1⋂S2⋂S3+…+Sm−2⋂Sm−1⋂Sm)+…+(−1)m−1(⋂i=1mS)
而求n中被一个质数整除的个数,可以直接用n/p得到,不用遍历整个n。
十、博弈论
公平组合游戏:
1.由两名玩家交替行动
2.在游戏进行的任意时刻,可以执行的合法行动与轮到哪位玩家无关
3.不能行动的玩家判负
游戏中的实际上每个点只有两种状态可能:必胜状态和必败状态,每次操作只能从必胜状态转到必败状态或从必败转到必胜或从必败到必败,无法一次操作从必胜状态转到必胜状态。因此在双方都理智的情况下先手存在必败或必胜状态。
如拿石子,最后不能走的状态是异或和为0,而每一步异或和为0的状态都无法通过拿走一定数量的石子把状态再变成0(0异或任何非零数都是非0),而石子数量是逐渐减少的,也就是说一定会走到终点,因此利用异或解决nim游戏是一个有效方法。
1.nim游戏: 算出所有石子堆的异或和x,若为0则先手必败,若非0则先手必胜(从非0转到0的方法:其实就是再异或一个x,因此要从大于x的石子堆a中拿走a−a⊕x 个石子,这样就还剩下a⊕x,最后的异或和即为0。
2.台阶nim游戏:由于偶数级台阶的石子不直接影响胜负关系(需至少进行偶数次操作才能到地面,所以若改变偶数级台阶的石子数量,下一个人只需要进行相同操作就可以保证胜负状态不变),因此台阶nim游戏实际上就是奇数台阶的nim游戏,奇数台阶异或和为0则先手必败,否则必胜(后手改变奇数台阶石子时,按照nim游戏操作即可,改变偶数台阶石子时先手只需复制后手的操作将石子拿到下一级台阶即可)
3.集合nim:sg函数:一个点的sg值是他去掉所能到的所有点的sg值中最小的自然数(能走到0的则不是0,不能走到0的一定是0,因此同样也是0和非0之间转换),终点的sg值是0。
利用sg函数可以把多个有向无环图当做经典nim游戏,通过图之间sg值的异或来判断先手是否必胜(SG函数的值表示的是能够走到所有小于且不等于该值的点,类似于拿石子,因此可当成nim游戏,终点是所有图都走到不能走的节点,即为全0)。当nim游戏中可操作的石子数属于一个集合时,就可以用可操作性的集合把每堆石子操作的状态生成一个拿走石子操作的有向无环图,确认每堆的sg值,再异或即可得到先手是否必败。
4.拆分nim游戏:一堆石子拆分成两堆,相当于一个局面拆分成了两个局面,由SG函数理论,多个独立局面的SG值,等于这些局面SG值的异或和。因此拆分nim游戏可看成集合nim游戏,所有可操作的状态为可分成的两堆状态不同的数量。