环的定义

确实，如果没有接触过环的概念，那么第一印象就是一个圈，也就是如果出现一个题，询问环的入环节点时

通常会很懵逼的：一个完整的圈，哪哪都是入口，这道题有病？

直到…你看了环的相关原理之后，你才会恍然大悟：哦，原来是这样。

随便找一篇文章：

https://blog.csdn.net/lym940928/article/details/88878425

我们直接来看一张图：

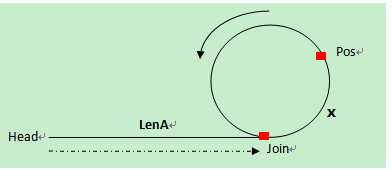
也就是说，“环”并不一定就是一个圈，可能还带着个尾巴。

详细定义： 就看图呗，反正我没找到，反正楼上这张图统称为带环问题。

对于带环问题，通常比较关注的几个角度分别是：

1.判断是否为环

2.求环长度

3.判断环的入口

对于第一个问题，判断是否为环，典型的方案就是快慢指针的方案，我比较喜欢称为刘翔超圈问题。

也就是你和刘翔一起跑圈，你们一定会照面几次。原因就是刘翔超圈了。

先假设构造一个环：

public class ListNode {
    public int val;
    public ListNode next;
    public String sVal;
    public ListNode(String sVal){
        this.sVal = sVal;
    }
    public ListNode(){}
}

public static ListNode createCircle(){

        ListNode A = new ListNode("A");
        ListNode B = new ListNode("B");
        ListNode C = new ListNode("C");
        ListNode D = new ListNode("D");
        ListNode E = new ListNode("E");
        ListNode F = new ListNode("F");
        ListNode G = new ListNode("G");
        ListNode H = new ListNode("H");
        A.next = B;
        B.next = C;
        C.next = D;
        D.next = E;
        E.next = F;
        F.next = G;
        G.next = H;
        //环
        H.next = C;
        return A;
    }

双指针判定这个环究竟是不是：还是比较简单的，快慢指针在存在环的单链表里面，一定会相遇

    public boolean judgeCircleExit(ListNode head){

        ListNode lower = head;
        ListNode faster = head;

        while (faster!= null&&faster.next!= null&&faster.next.next!= null){
            lower = lower.next;
            faster = faster.next.next;
            if(lower.equals(faster)){
                return true;
            }
        }
        return false;
    }

另外一个问题：求环长

1.先确定第一个相遇的位置为0，然后再次相遇时，显然，faster走的路程是lower的两倍，换个角度想：当再次相遇时，faster比lower多跑了一圈

    /**
     * 求环长度
     * @param head
     * @return
     */
    public int countCircleLen(ListNode head){

        ListNode lower = head;
        ListNode faster = head;
        /**
         * statu = 0:未相遇
         * statu = 1:第一次相遇
         * statu = 2:第二次相遇(结束)
         */

        int statu = 0;
        int len = 0;
        while (faster!= null&&faster.next!= null&&faster.next.next!= null){
            lower = lower.next;
            faster = faster.next.next;
            if(lower.equals(faster)){

                Debug.Log(statu);
                statu++;
                if(statu == 2){
                    break;
                }
            }
            if(statu==1){
                len++;
            }
        }
        return len;
    }

求环的入口

这是一个数学题…

https://blog.csdn.net/qq_36781505/article/details/91401474

解决思路也比较简单，参考它的代码就行

    public ListNode getEntrance(ListNode head){
        ListNode faster = head;
        ListNode lower = head;
        while (faster!= null&&faster.next!= null){
            lower = lower.next;
            faster = faster.next.next;
            if(lower == faster){
                //第一次相遇在p1点
                break;
            }
        }
        //让faster回到p0点
        faster = head;
        //经过m圈后，faster和lower(以步长为1行走)将会在经过m圈后在
        // p3也就是entrance点相遇
        while (faster!= lower){
            lower = lower.next;
            faster = faster.next;
        }
        return faster;
    }

嗯，然后来找bug

1.上述代码默认了一定存在环的情况，而如果环不存在的话，那么得返回null是吧

显然的，上面没有返回

判断不存在环，只要不相遇就成

    /**
     * 求环的入口
     * @param head
     * @return
     */
    public ListNode getEntrance(ListNode head){
        ListNode faster = head;
        ListNode lower = head;
        boolean flag = false;
        while (faster!= null&&faster.next!= null){
            lower = lower.next;
            faster = faster.next.next;
            if(lower == faster){
                //第一次相遇在p1点
                flag = true;
                break;
            }
        }
        //不相遇的情况
        if(!flag){
            return null;
        }

        //让faster回到p0点
        faster = head;
        //经过m圈后，faster和lower(以步长为1行走)将会在经过m圈后在
        // p3也就是entrance点相遇
        while (faster!= lower){
            lower = lower.next;
            faster = faster.next;
        }
        return faster;
    }