博客

模拟退火算法用于解决最优化问题

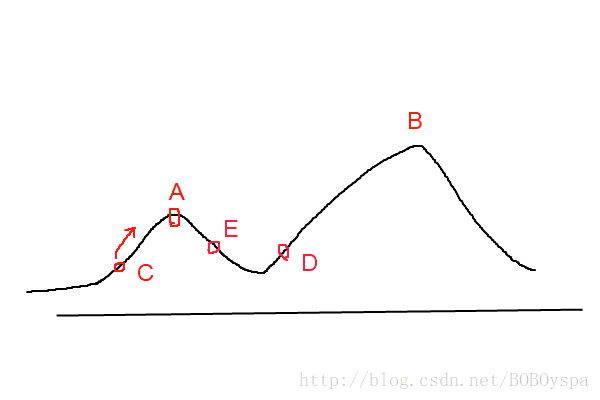
爬山算法（一种完全的贪心搜索算法），每次向着当前上升速度最快的方向向上爬，最后的最优解取决于初始点，容易陷入局部最优解困境，如图，若起始点选择在C处，当算法到达A点时候将停止寻找，因为在A点附近没有任何上升的机会。模拟退火算法则用于尝试解决这个问题

过程中：目标函数 作为 能量函数

算法思想：模拟退火算法以一定的概率接受一个比当前解要差的解（这个概率随着时间的推移逐渐降低），最后就有可能跳出局部最优解从而达到全局最优解

算法伪代码：

T：系统当前的温度

min_T：温度下限

Y(i)：当前状态

Y(i+1)：新状态

J(y)：表示在状态y时的评价函数值（能量函数）

r：控制降温快慢

While(T > min_T)
{
    dE = J(Y(i+1))-J(Y(i))
    if(dE >= 0)：
        Y(i+1) = Y(i) //若移动后的状态比之前好，则接受移动
    else:
        if(exp(dE/T)>random(0,1)):
            Y(i+1) = Y(i) //接受移动
    T = r * T //降温退火
    i ++
}

一个模拟退火算法例子

计算列表元素的最大值

from random import randint
import math
import random

'''模拟退火算法选择列表中的最大值'''
def simAnnealingMAX(lst,howfar):
    '''
    lst是待确定最大值的列表
    howfar是每次前进时能够看到的最远方，当然越大算法越准确
    '''
    assert howfar>1,'parameter "howfar" must > 1'
    # 从列表中的第一个元素开始
    # 如果已经到达最后一个元素或者找到局部最大值，算法结束
    start = 0
    length = len(lst)
    times = 1# 随机游走次数

    while start <= length:
        # 当前局部最优解
        m = lst[start]
        # 下一个领域内的数字
        loc = lst[start+1:start+howfar]
        # 如果已经处理完所有数据，则结束
        if not loc:
            return m
        # 达到下一个里领域内的局部最优解及其下标
        mm = max(loc)
        mmPos = loc.index(mm)
        # 如果下一个领域内有更优的解，Go!
        if m <= mm:
            start += mmPos + 1
        else:
            # 如果下一个领域内没有更优解，以一定的概率前进或结束
            delta = (m-mm)/(m+mm)
            # 随机游走的次数越多，对概率要求越低
            if delta < random.random()/times:
                start += mmPos + 1
                times += 1
            else:
                return m

lst = [randint(1,200) for i in range(200)]
print('最优解最大值：',max(lst))
print('局部最优解:',simAnnealingMAX(lst,10))