MATLAB做晶体结构图(固体物理).md
写在前面
最近在复习考研复试《固体物理》这一门课,去年学的内容已经忘干净了,所以就翻开前几页。突然看到了面心立方和体心立方结构图,想到了去年室友用Mathematica做了晶胞的结构图,于是就手痒痒自己也想来做一个。
具体物理内容不会涉及到多少,但还是要求大家能对“简单立方结构”、“体心立方结构”、“面心立方结构”有一个简单的理解,因为我比较懒,所以我就不放这些基础内容凑字数了。
用MATLAB跑出来的效果图为
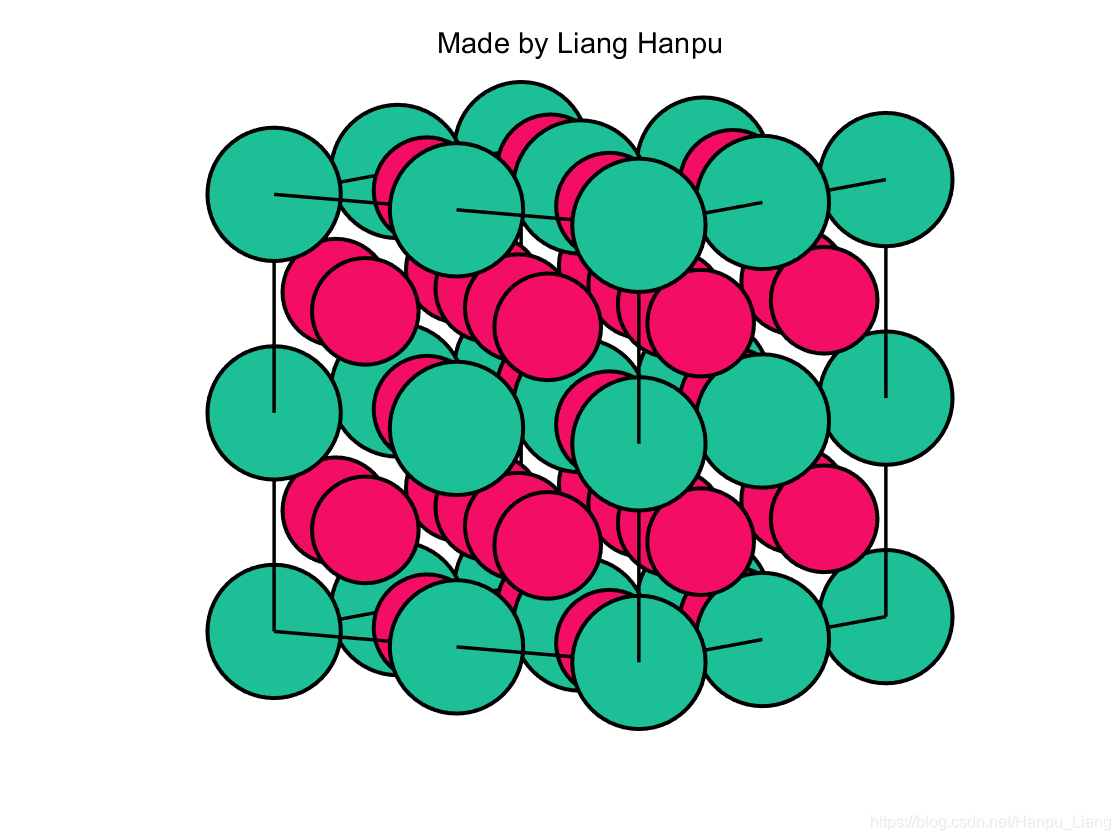
我的所有程序都放在我的Github: https://github.com/HanpuLiang/Something-Small中,点击即可查看。
基本的思考
如果我们想要做一个类似于这样子的结构图的话,我们需要知道些什么?
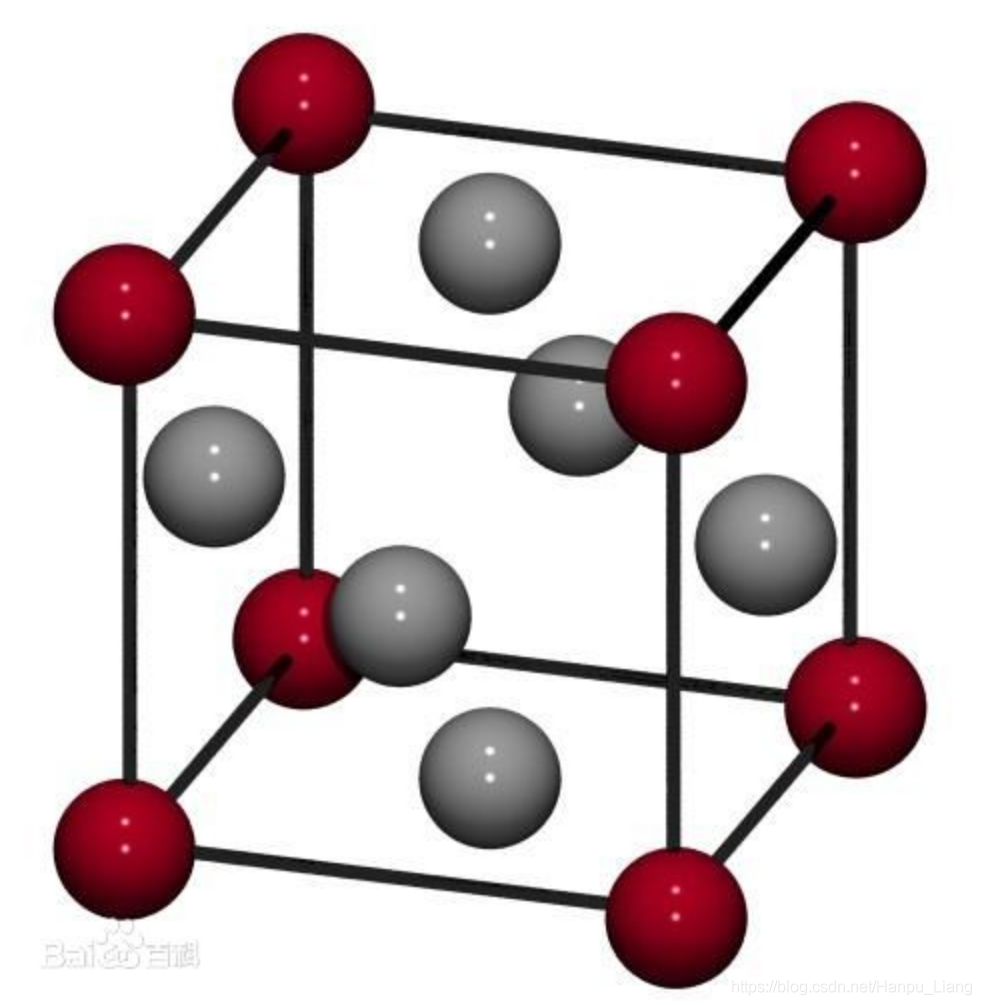
如果我们想要做成这么大个超胞的话,又需要在上面的基础上怎么做?
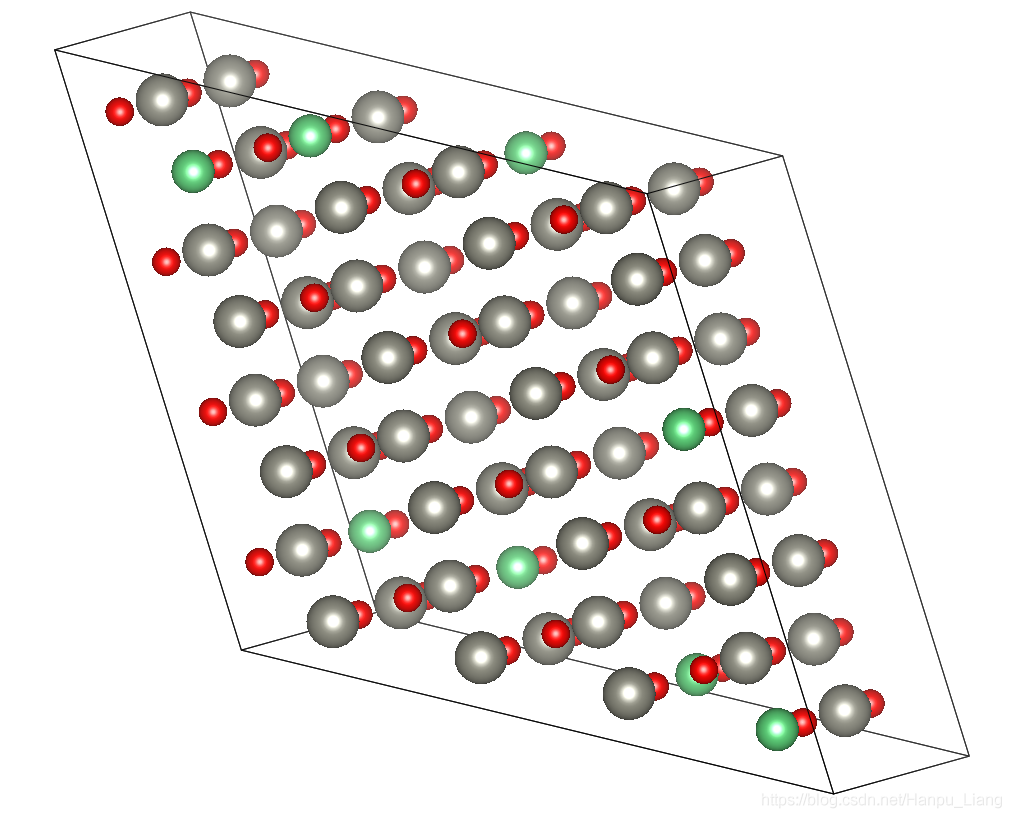
有过做计算的同学已经想到了,需要计算物理中,描述晶胞中原子位置的文件POSCAR,然后把POSCAR拖到VESTA中就可以上面这幅图了。
所以我们这里模拟POSCAR来输入参数:
- 晶胞参数:描述晶胞大小的参数。
- 超胞大小:当晶胞数量大于1个并且周期性变化时,用三个数字描述其在三个方向上的晶胞叠加数目。
- 各个原子的坐标:没有这个还怎么画出来原子啊。
基本参数
晶胞参数
晶胞参数包括6个值:三条边
a
1
,
a
2
,
a
3
a1, a2, a3
a1,a2,a3和三个角
α
,
β
,
γ
\alpha, \beta, \gamma
α,β,γ,如下图所示
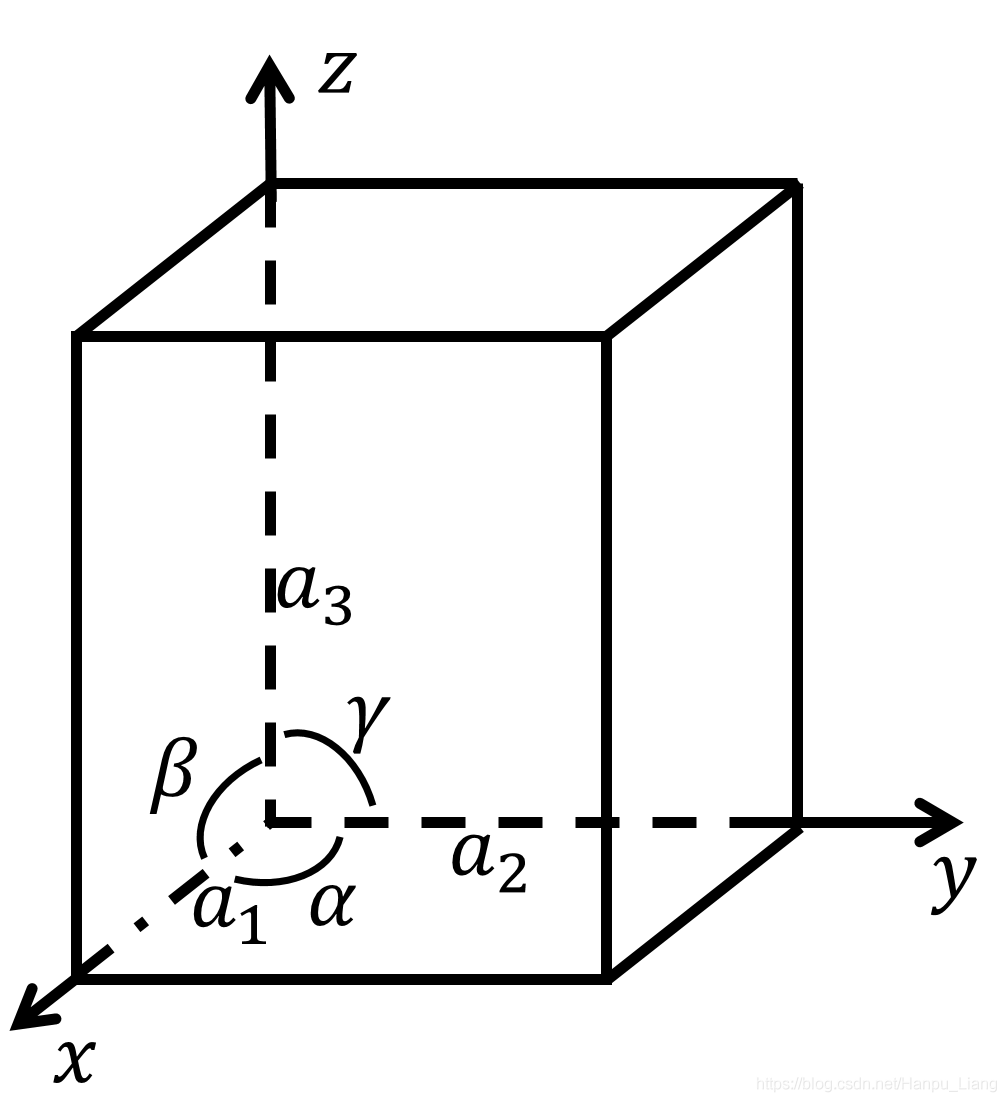
因为编写程序的复杂程度问题,我们这里只考虑
α
≠
9
0
o
,
β
=
γ
=
9
0
o
\alpha\neq 90^o, \beta=\gamma=90^o
α̸=90o,β=γ=90o这样的情况。如果不这样的话,那就有点难了,需要考虑这个晶胞斜向的角度。
超胞大小
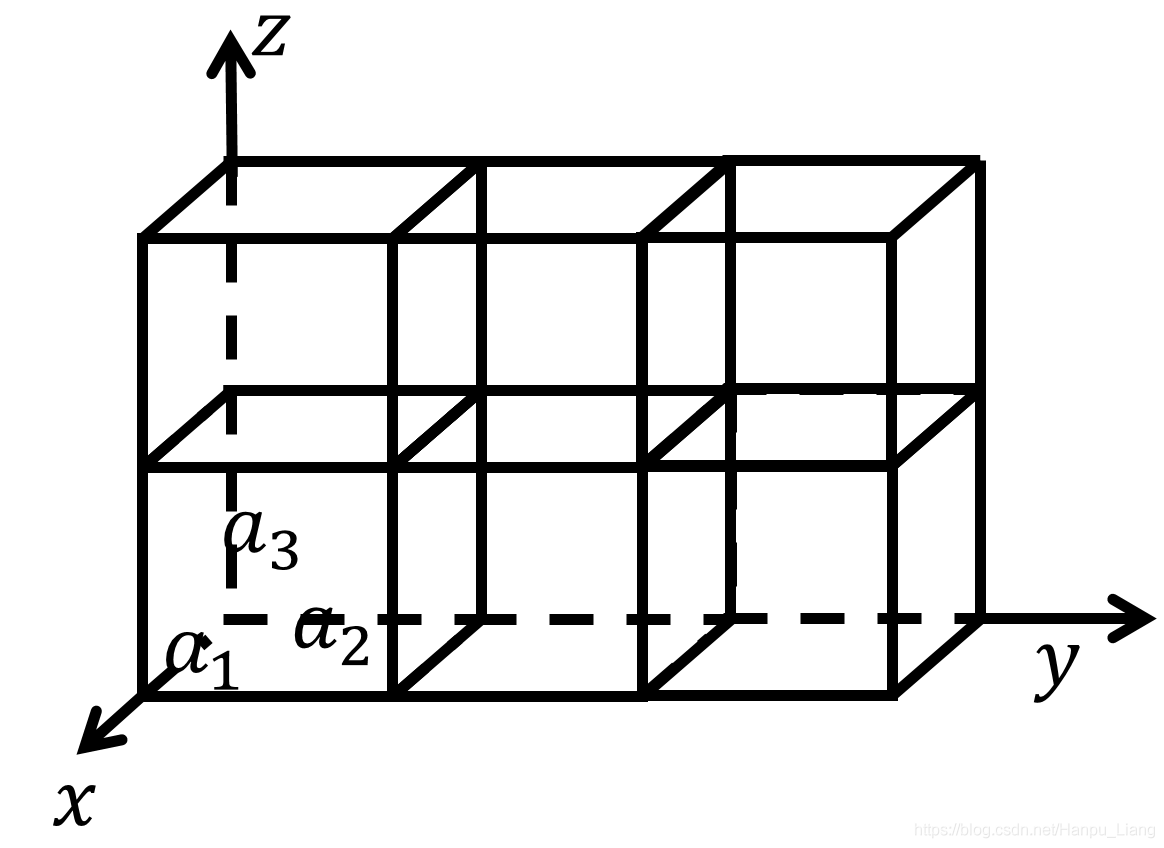
超胞大小是用来形容我们这个超胞到底由几个晶胞组成,以及他们的排列方式是怎么样子的。就比如下图中,沿着a1方向的层数为1个,沿着a2方向的层数为3,沿着a3方向的层数为2.所以我们就可以设定为
[
1
,
3
,
2
]
[1, 3, 2]
[1,3,2]。
**值得注意的是,这里我用的并不是
x
,
y
,
z
x, y, z
x,y,z轴的方向!!!**因为如果
α
≠
9
0
o
\alpha\neq 90^o
α̸=90o的话,那么a2方向就不和y轴平齐了,所以为了保证两个晶胞相连,就必须要沿着晶轴方向拓展。
原子位置
这个没什么好说的,如果我们建立好了超胞,那么直接在对应的坐标画上原子就好。
开始写程序
设定参数
首先我们来设定好上面的参数
%% 参数设定
global cell_size a1 a2 a3 alpha beta gamma
% 晶胞参数
a = [1, 1, 1];
% 三个角度
angle = [pi/2, pi/2, pi/2];
% 超胞大小
cell_size = [2, 2, 2];
% 简单立方
position1 = [0, 0, 0; ...
1, 1, 0; ...
1, 0, 0; ...
0, 1, 0; ...
0, 0, 1; ...
1, 1, 1; ...
1, 0, 1; ...
0, 1, 1];
% 体心
position2 = [0.5, 0.5, 0.5];
% 面心
position3 = [0, 0.5, 0.5; ...
0.5, 0, 0.5; ...
0.5, 0.5, 0; ...
1, 0.5, 0.5; ...
0.5, 1, 0.5; ...
0.5, 0.5, 1];
[a1, a2, a3] = deal(a(1), a(2), a(3));
[alpha, beta, gamma] = deal(angle(1), angle(2), angle(3));
这里将体心和面心的原子分别提取出来,作图的时候再放上去和简单立方的一起做就好了。
作图
我们为了图像美观就得做一些处理坐标轴的事情
%% 作图
figure
% 作图设置
hold on, axis equal
axis image off
view(-37.5, 30)
然后我们就可以愉快的画超胞的框架和各个原子啦,下面的两个函数是我自定义的两个函数
% 做超胞框架
plotBox();
% 做各个原子
plotAtoms(position2, [244, 13, 100]/255, 40);
plotAtoms(position1, [29, 191, 151]/255, 50); %简单立方的一定要放在最后面
简单立方因为最大,所以我在里面设定了一些自动变坐标轴大小的内容,所以要放在最后面。
这样子主程序就完成了。后面详细解释这两个函数的内容。
做超胞的框架plotBox
我们需要定出立方体的8个顶点,然后做出12条边,这一部分很简单,根据简单的数学就可以推导出公式,然后写出程序来。
function plotBox()
% 做边框
global a1 a2 a3 alpha beta gamma cell_size
% 超胞的边长
[A1, A2, A3] = deal(a1*cell_size(1), a2*cell_size(2), a3*cell_size(3));
% 8个顶点
vertex = [0, 0, 0;...
A1, 0, 0;...
A2*cos(alpha), A2*sin(alpha), 0;...
A2*cos(alpha)+A1, A2*sin(alpha), 0;...
0, 0, A3;...
A1, 0, A3;...
A2*cos(alpha), A2*sin(alpha), A3;...
A2*cos(alpha)+A1, A2*sin(alpha), A3];
% 12个边
plotLine(vertex(1,:), vertex(2,:))
plotLine(vertex(1,:), vertex(3,:))
plotLine(vertex(2,:), vertex(4,:))
plotLine(vertex(3,:), vertex(4,:))
plotLine(vertex(5,:), vertex(6,:))
plotLine(vertex(5,:), vertex(7,:))
plotLine(vertex(6,:), vertex(8,:))
plotLine(vertex(7,:), vertex(8,:))
plotLine(vertex(1,:), vertex(5,:))
plotLine(vertex(2,:), vertex(6,:))
plotLine(vertex(3,:), vertex(7,:))
plotLine(vertex(4,:), vertex(8,:))
end
function plotLine(x1, x2)
% 做两个点之间的框架线
plot3([x1(1) x2(1)], [x1(2), x2(2)], [x1(3), x2(3)], 'k', 'linewidth', 1.3)
end
做各个原子的图
这个才是重头戏。
我们首先要确定出在超胞内,一共有多少个原子。我们之前设置的超胞大小就派上用场了,我们通过三个循环嵌套在一起,遍历出超胞内的所有晶胞,然后将其原子位置加到矩阵中,最后统一作图。
function plotAtoms(position, markercolor, markersize)
% 做各原子图像
global cell_size a1 a2 a3 alpha beta gamma
% 原始晶胞
% plot3(position(:,1), position(:,2), position(:,3), 'ok', 'linewidth', 1.5, 'markersize', 50, 'markerfacecolor', [29,191,151]/255)
% 超胞
% 遍历得到超胞所有原子
cur_point = position;
for i1 = 1:cell_size(1)
for i2=1:cell_size(2)
for i3=1:cell_size(3)
x_plus = a1*(i1-1) + a2*cos(alpha)*(i1-1);
y_plus = a2*sin(alpha)*(i2-1);
z_plus = a3*(i3-1);
cur_point = [cur_point; [position(:,1)+x_plus position(:,2)+y_plus position(:,3)+z_plus]];
end
end
end
plot3(cur_point(:,1), cur_point(:,2), cur_point(:,3), 'ok', 'linewidth', 1.5, 'markersize', markersize, 'markerfacecolor', markercolor)
% 设置坐标轴大小
[x_min, x_max, y_min, y_max, z_min, z_max] = deal(min(cur_point(:,1)), max(cur_point(:,1)), ...
min(cur_point(:,2)), max(cur_point(:,2)), ...
min(cur_point(:,3)), max(cur_point(:,3)));
x_len = (x_max - x_min)/6;
y_len = (y_max - y_min)/6;
z_len = (z_max - z_min)/6;
axis([x_min-x_len x_max+x_len y_min-y_len y_max+y_len z_min-z_len z_max+z_len])
end
然后这样就完事了。是不是很简单的。
写在后面
以上所有代码我都放在了我的Github中,可以通过点击我的Github: https://github.com/HanpuLiang/Something-Small去查看。代码下载后可直接运行。
如果喜欢的话,麻烦点个关注,给个赞,加个收藏噢。