前言

数字信号和图像处理中经常用到的样本位置的移动主要是通过插值实现的。根据采样定理，在满足

1）信号是带限的，即最高频率有界；

2）满足奈奎斯特采样率，即实信号的采样率高于最高频率的两倍、复信号采样率高于信号带宽。

以上两个条件时，就可以通过卷积重建初始信号。因此，插值可以通过卷积实现

其中，h(x)称为插值因子或插值核。i处的样本被核h(i-x)加权，插值点x处的g(x)等于x邻域样本的加权和。

一、sinc插值的原理

对于sinc插值，卷积核是sinc函数

插值信号为

即为所有输入样本的加权叠加。

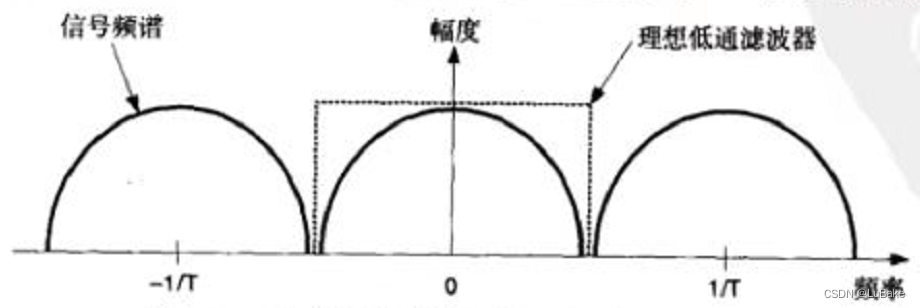
上式可通过频域来理解，采样信号的频谱等于以采样率重复的信号频谱。为了重建信号，只需要一个周期的频谱（如基带周期），因此需要理想矩形低通滤波器在频谱提取基带频谱。矩形低通滤波器（门函数）在时域中是sinc函数。由于频域相乘相当于时域卷积，故插值可以通过与sinc核卷积来实现。

图给出了g(x)在x=11.7处插值的示例。a为连续sinc插值函数，b中的插值核以x=11.7为中心。在计算完采样点处的权值（星号）后，根据插值公式得到数据点的加权和。插值结果如图c菱形所示。

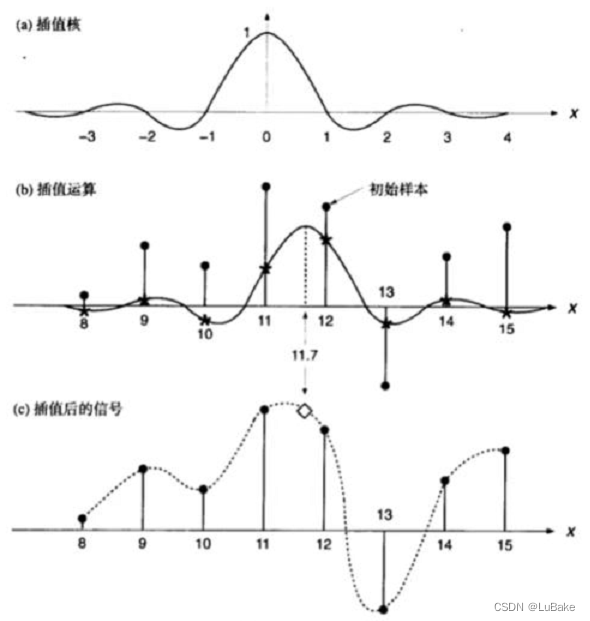
需精确计算某一点上的g(x)，卷积核需要覆盖无限多个点。实际上这是无法做到的，而且十分耗时。不过，核值随着与x的间隔增大而降低（中心向两侧衰减），这意味着可以不过度损失精度的情况下对卷积核进行截断。上图中，卷积核限制为8个点，g(11.7)通过8~15这8个采样点计算得到。

同时为了提高计算效率，可以将升采样后的插值核存储在表格中，这样就无需对每个插值点计算sinc函数，而只需要使用最接近移动位置处的表格系数（查表的方式）。核长以及表格中的升采样点数都对精度有所影响。表格的尺寸限制最多会引入一个1/2升采样间隔的几何误差。

下表给出了一个插值系数表格的例子。量化位移为采样点的1/16。一定位移下的插值系数可以从表格中的相应行得到。每行中的8个系数定义了一个具体的插值因子。第一行为平移0采样点时的系数，第二行为平移1/16采样点时的系数，…，第十六行为平移15/16个采样点时的系数，第十七行为平移1个采样点时的系数（增加第17行是为了计算15/16+1/32~1位置的插值点方便）。

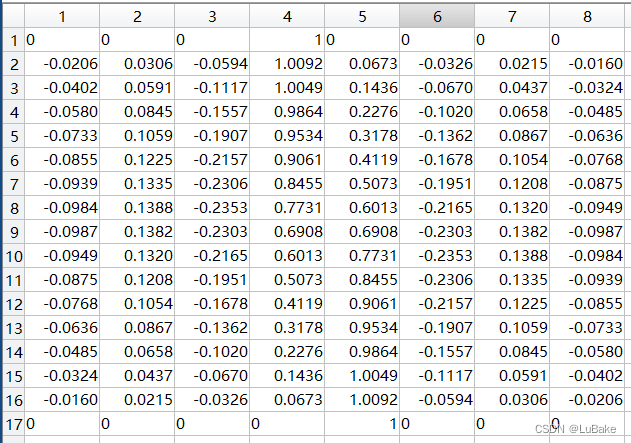
以插值位置11.7为例，首先取整数点位置11，用来选取待加权的采样点，选取包含11在内的左侧4个采样点（8、9、10、11）、右侧四个采样点（12、13、14、15）共8个采样点。再选取小数点位置0.7，用来选取插值因子，0.7*16四舍五入（11）得到最接近的量化位置，即选表中的第12（11+1）行。由此根据卷积公式通过计算加权和即可计算的大插值点的值。

二、sinc插值的实现

根据上述介绍的原理，在matlab中进行实现，代码如下

clc;close all;
%构造插值表
intp_num = 8; %插值点数
quant_num = 16; %量化点数
x_org = -intp_num/2+1:intp_num/2;
sinc_tab = zeros(quant_num+1,intp_num);
for i = 0:quant_num
   x = x_org - i/quant_num;
   sinc_tab(i+1,:) = sinc(x); 
   sinc_tab(i+1,:) = sinc_tab(i+1,:)./sum(sinc_tab(i+1,:)); %归一化
end

%原始采样信号
N=128;
n=1:N;
f0=50;
f1=200;
fs=2e3;
y=sin(2*pi*f0.*n/fs)+2*sin(2*pi*f1.*n/fs);

%待插值位置
x_intp = [19.7 20.8 30.6 40.5 90.7];%[11.7 12.8 19.6 40.5 90.7];
y_intp = zeros(1,length(x_intp)); %插值后的值

x_intp_int = floor(x_intp); %计算整数点
x_intp_dec = x_intp - x_intp_int; %计算小数点
x_intp_pos = round(x_intp_dec*quant_num)+1; %计算插值表索引
   
%计算卷积
for j = 1:length(x_intp)
   y_intp(j) = dot(sinc_tab(x_intp_pos(j),:),y(x_intp_int(j)-intp_num/2+1:1:x_intp_int(j)+intp_num/2));
end

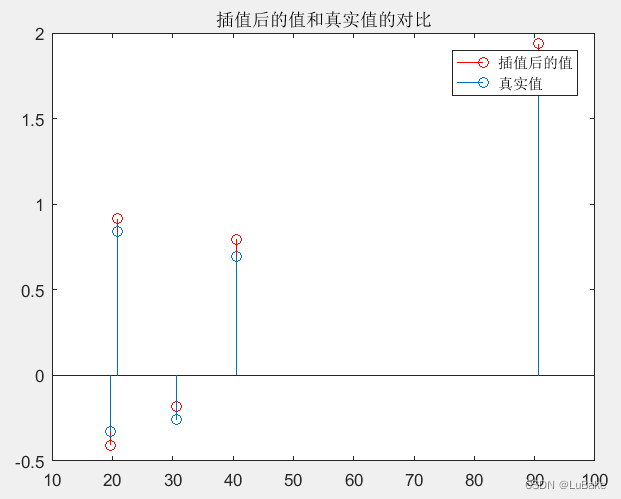
figure;stem(x_intp,y_intp,'r');hold on;

%计算真实值
y_org = sin(2*pi*f0.*x_intp/fs)+2*sin(2*pi*f1.*x_intp/fs);
stem(x_intp,y_org); title('插值后的值和真实值的对比');legend('插值后的值','真实值');

仿真结果如下，可看出插值后的值存在一定的量化和截断误差。