卷积神经网络是深度学习最核心的部分;
最早用于美国银行系统识别手写支票;
卷积神经网络
一、训练数据
因为卷积神经网络是为了解决图像领域的应用而提出的网络结构,所以训练数据一般为视频图像数据(张量数据,tensor);可以根据图像的性质对CNN的结构进行设计,使得CNN相比一般的神经网络结构更加高效、性能更好。
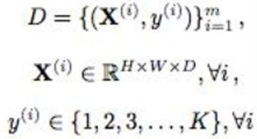
其中:
X(i)是第i张图像;
H * W * D是每个图像的尺寸;
D表示整个训练集,也表示图像的深度;
二、网络层次
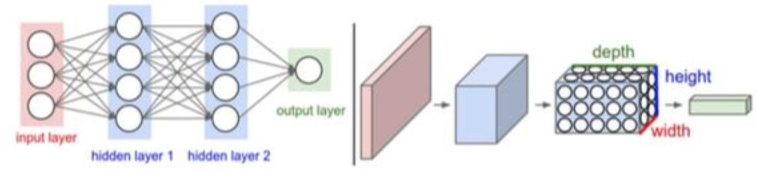
上图中左侧(普通神经网络)中每一层的神经元按一个维度排成向量;
而右侧(CNN)的输入变成了张量,即每层神经元按三个维度(高H、宽W、深D)排成张量,最后一层的神经元输出维度是1 * 1 * K(K表示最终分类的类别数);
普通神经网络每层都是一个全连接层(仿射运算 + 非线性变换);
而CNN每层都有4中选择:卷积层(convolutional layer,conv)、池化层(pooling layer,pool)、线性整流层、全连接层(fc);
卷积层(convolutional layer,conv)
:通过卷积核做卷积变换(线性变换)提取特征的响应,将卷积核代表某种特征,得到的结果叫特征响应图,相似度越高得到的响应越大;
卷积层的简化——稀疏连接:在图像识别中,关键性特征(边缘、角点等)只占了图像的一小部分,图像中相距很远的两个像素间相互有影响的可能很小,全连接就是一种资源的浪费,所以产生了稀疏连接,每个神经元只需要和一小部分输入神经元相连,大大降低了数据量、计算量。
局部连接的空间范围称为感受野,而沿深度轴的连接数总是等于输入的深度D(即沿高、宽轴是局部连接的,沿深度轴是全连接的)。
稀疏性是CNN相比一般神经网络的一个巨大优点,极大降低了模型的计算量。
实际操作中,卷积核一边做卷积运算,一边沿着高和宽滑动(如下图):
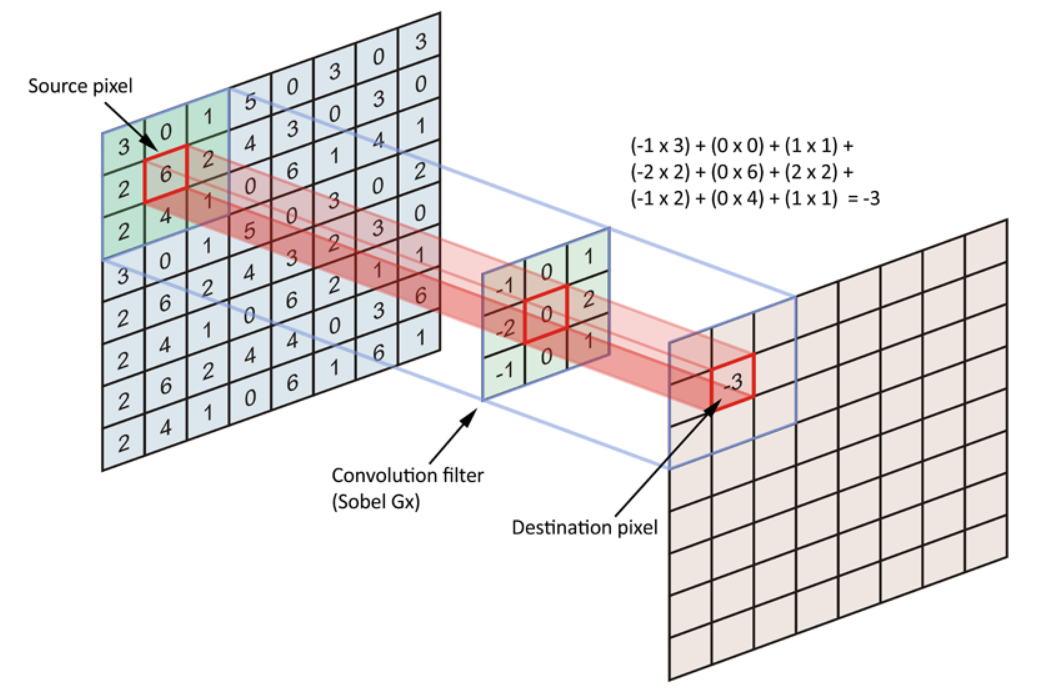
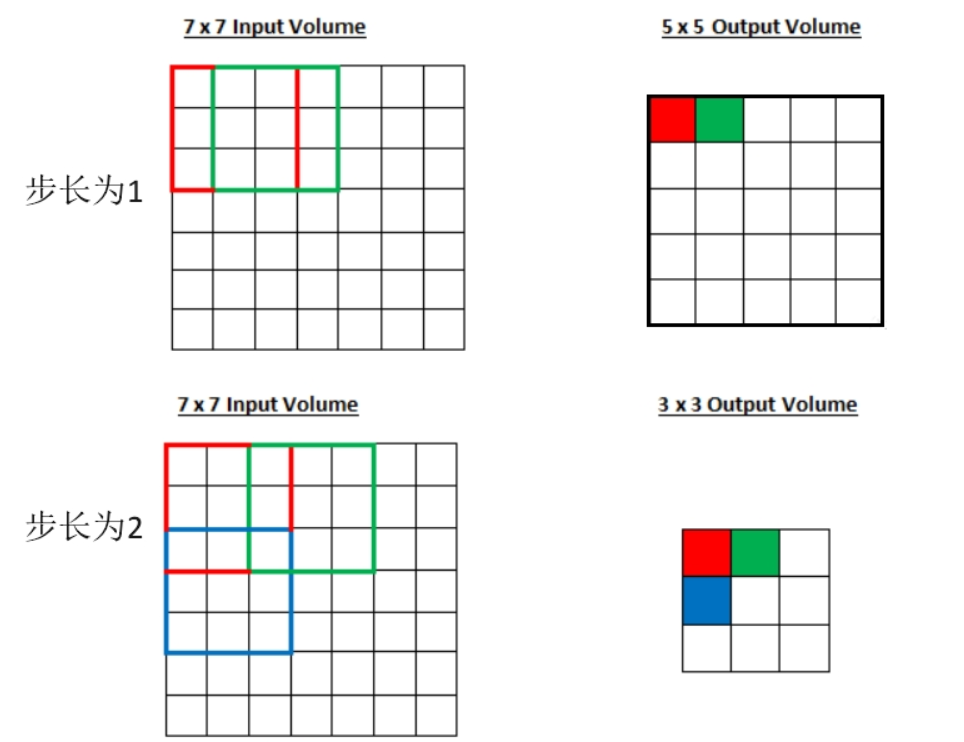
卷积层的简化——共享参数:如果一组权重(即卷积核)在图像中某个区域提取有效表示,也能在另外区域提取有效表示。
即卷积核与所滑动到的图像任一区域对应相乘求和(卷积操作),卷积核是不变的,相当于卷积核所在区域与同一套权重相乘。大幅减少了参数数量。
一般用4个量来描述卷积层:
1、滤波器filter(即卷积核)的数目D1;
2、滤波器感受野F1 * F2:即滤波器的尺寸;
3、步幅(stride)S:在一个激活映射中,在空间上每跳过S个位置计算一个输出神经元,即上图中的步长;
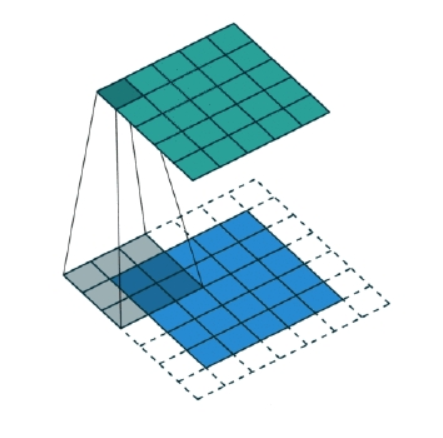
4、0填充(zero-padding)P:在进行卷积前,四周填充一些0,填充的宽度为P,这可以控制输出特征映射的大小(如下图):蓝色区域为原图像大小,虚线部分为填充(此处P=1),绿色为输出特征映射。
池化层(pooling layer,pool)
:相当于大脑视觉皮层中的复杂细胞,模拟感受野;
池化层根据神经元空间上局部统计信息进行采样,在保留有用信息同时减少神经元空间大小,使参数量减少并降低了过拟合可能;
pool操作在各深度分量上独立进行;
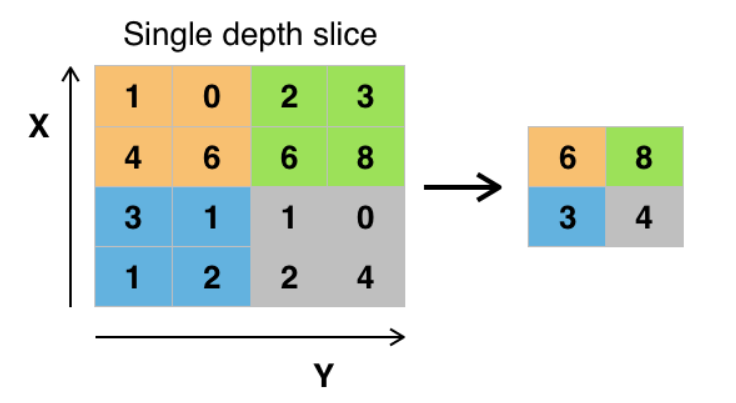
最常用的是最大池化(max-pooling)、滤波器大小为2 * 2,步幅为2,这可以舍弃75%的信息,如下图:
线性整流层
:激活函数层,常用relu;
与一般神经网络中的激活函数操作相同,如使用relu时,逐元素进行relu操作,不会改变维度;
通过激活函数实现了非线性变换;
使用relu激活函数也是使网络快速收敛的一个手段,大于0时梯度为1,避免了梯度弥散与梯度消失。
全连接层(fc)
:层与层之间每个神经元都有连接。与一般神经网络操作相同。
三、损失函数
损失函数度量的是模型预测值与真实值之间的误差(这里叫损失函数或代价函数,在优化时会使其最小化,这个需要最小化的函数叫目标函数);
通过损失函数的优化来实现整个系统的优化,损失函数的设计不仅定义了问题,还直接决定了优化算法收敛的性能;
(损失函数总结笔记后续整理)
四、优化
使损失函数(目标函数)最小化。
与一般神经网络同样使用梯度下降法(前向传播、反向传播),不同点在于池化层与卷积层的反向传播操作。
卷积层的反向传播:利用链式求导法则,用损失函数分别对W、b、X求偏导,计算如下图(重在理解):
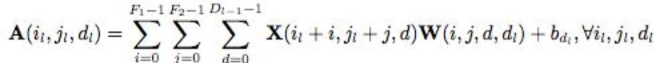

池化层的反向传播:池化层没有参数,不需要进行参数更新,因此池化层在反向传播时需要完成的工作是将第L层的导数传播到第L-1层,以最大池化为例:
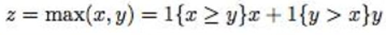
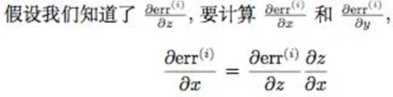
上图不太清楚,内容描述的是 假设知道了损失函数对z的导数,要计算对x、y的导数,依然使用链式法则即可。
五、预测
对于一个未知输入数据x,分类模型的预测是:
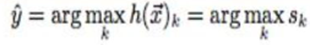
即:找到分类器输出分数最大的那项对应的类,作为x的标记。
如:共有三个类别A、B、C,对应分数为(0.1, 0.6, 0.3),其中0.6最大,那么就预测x属于B类。
六、评估
简单来说就是,用 预测正确的样本数占样本总数的比例 来评估模型。
具体如下:
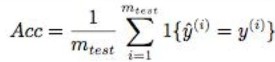
其中:
m为测试集样本总数;
I{*}为指示函数,预测值与真实值相等时,指示函数为1,否则为0。
从上式可知,测试集全部分类正确时,Acc = 1,否则Acc < 1。