顶点之间的通路数量
这个证明我暂时先搁置一下,先说结论,一个图中,长度为k的回路(不是简单回路)的数量,等于该图所代表的矩阵的k次乘积后所对应位置的值。
比如下面的这张图:
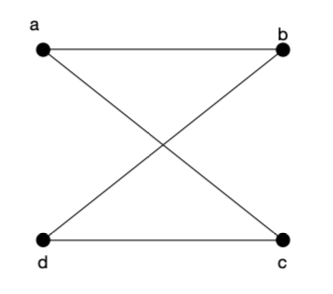
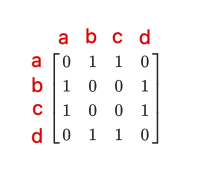
对应的矩阵为:a,b,c,d
[
0
1
1
0
1
0
0
1
1
0
0
1
0
1
1
0
]
\left[ \begin{matrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{matrix} \right]
⎣
⎢
⎢
⎡
0
1
1
0
1
0
0
1
1
0
0
1
0
1
1
0
⎦
⎥
⎥
⎤
即:
然后矩阵乘以其自身8次后,结果为:
[
8
0
0
8
0
8
8
0
0
8
8
0
8
0
0
8
]
\left[ \begin{matrix} 8 & 0 & 0 & 8 \\ 0 & 8 & 8 & 0 \\ 0 & 8 & 8 & 0 \\ 8 & 0 & 0 & 8 \end{matrix} \right]
⎣
⎢
⎢
⎡
8
0
0
8
0
8
8
0
0
8
8
0
8
0
0
8
⎦
⎥
⎥
⎤
然后假设求a-d之间的回路数量,即为8:
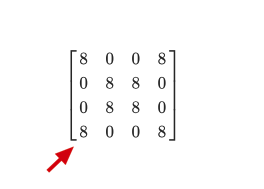
具体的值为:
- a,b,a,b,d
- a,b,a,c,d
- a,b,d,b,d
- a,b,d,c,d
- a,c,a,b,d
- a,c,a,c,d
- a,c,d,b,d
- a,c,d,c,d