一般性假币称重鉴别问题

问题重述

设有

$n$
枚硬币，其中仅有一枚假币，在已知或未知假币与真币之间重量关系两种情况下，通过无砝码天平称重的方法鉴别假币，求所需的最少称重次数。
问题分析

此问题是经典的信息论算法问题，许多大公司都曾以此作为面试、笔试题来考核员工。从信息论角度看，“有

$n$
枚硬币，其中仅有一枚假币”发生概率为

$P = \frac{1}{n}$
，“假币与真币之间重量关系未知”发生概率为

$P = \frac{1}{2}$
，为了确定哪一枚假币，即要消除上述事件的联合不确定性。

又因为两事件独立，因此有

${I_1} = \log n + \log 2 = \log 2n$
比特；用天平称重，有三种可能：平衡、左倾、右倾，三者等概率，为

$P = \frac{1}{3}$
，因此天平称重一次消除的不确定性为

${I_2} = \log 3$
比特，所以称重次数至少为

$\frac{{{I_1}}}{{{I_2}}} = \frac{{\log 2n}}{{\log 3}}$
次。
解题思路

【问题一】当

$n = 12$
时

将12个硬币编号为：1，2，3，4，5，6，7，8，9，10，11，12

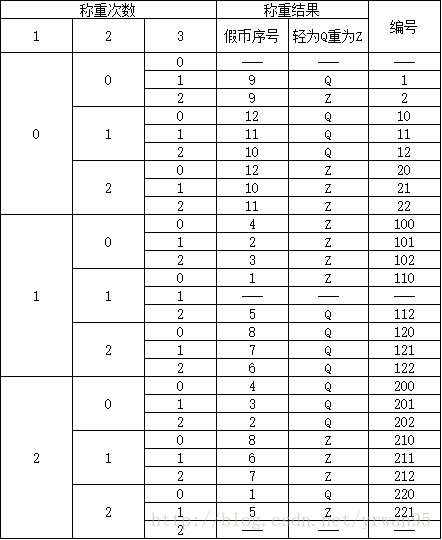
称重安排如下表：

称重结果表示为：0：平衡 1：左倾 2：右倾

可以得到如下表结果：

同理可用矩阵表示3次称重的安排，矩阵上方为硬币序号，矩阵的行为3次称重时矩阵的放置位置，1表示放到左盘，2表示放到右盘，0表示不参与称重。

1

2

3

4

5

6

7

8

9

10

11

12

⎛

⎝

⎜

1

1

0

1

0

1

1

0

2

1

0

0

2

2

1

2

1

1

2

1

2

2

1

0

0

0

2

0

2

1

0

2

2

0

2

0

⎞

⎠

⎟

$\begin{array}{l} {\kern 10pt}1{\kern 11pt} 2{\kern 10pt} 3{\kern 10pt} 4{\kern 10pt} 5{\kern 10pt}6{\kern 10pt}7{\kern 11pt}8{\kern 10pt}9{\kern 7pt} 10{\kern 6pt} 11{\kern 5pt} 12\\ \left( {\begin{array}{*{20}{l}} 1&1&1&1&2&2&2&2&0&0&0&0\\ 1&0&0&0&2&1&1&1&0&2&2&2\\ 0&1&2&0&1&1&2&0&2&1&2&0 \end{array}} \right) \end{array}$

由表格与矩阵，发现：如果检测结果与矩阵的某列符合，则对应序号的硬币即为假币，且重量较重；如果检测结果不在上述矩阵的列中，将1、2互换，得到假币对应序号，重量较轻。例如，若称重结果为110，则1号为假币，且重量较重；若称重结果为201，将1与2互换，得到102，则3号为假币，且重量较轻。

【问题二】当

$n{\rm{ = }}39$
时

查阅资料可得，

$k$
次称重最多可以在

$\frac{{{3^k} - 3}}{2}$
个硬币中找到不同的硬币，并判断其轻重。已知硬币数量为39，可求得需要称量的次数

$k{\rm{ = }}5$
1. 编码
  
  以称量次数为编码长度，使用0、1、2排列组合进行编码，再去掉全为0、全为1和全为2，可知一共有
  
  ${3^k} - 3$
  个编码。在一个编码中，第一处相邻数字不同的情况是01、12或20，则我们称它为正序码，如11010；否则为逆序码，如11210；在长度为的编码中，正序码和逆序码的数量相等，为
  
  $\frac{{{3^k} - 3}}{2}$
  个。
2. 赋值
  
  如果把一个正序码的0换成1，1换成2，2换成0，则它认为正序码。由此，将正序码每3个分为一组，例如11010、22121、00202。7将正序码的0与2互换，即可得到一个逆序码，因此每枚硬币均有一个正序码一个逆序码。
3. 称重
  
  第一次，将正序码第一位为1的硬币放在左侧，为2的硬币放在右侧，其余不参与称重，如果天平平衡记为0，左倾记为1，右倾记为2；
  
  第二次，将正序码第二位为1的硬币放在左侧，为2的硬币放在右侧，其余不参与称重；
  
  每轮如此，重复次，结果得到一个位编码。如果此编码为某个硬币的正序码，则这个硬币比其余硬币重；如果此编码为某个硬币的逆序码，则这个硬币比其余硬币轻。
可视化演示

以

$n=12$
为例

（1）编号（假设6号硬币为假币）

（2）赋值

$123456789101112 ⎛ ⎝ ⎜ 110101102100221211212210002021022020 ⎞ ⎠ ⎟$
$\begin{array}{l} {\kern 10pt}1{\kern 11pt} 2{\kern 10pt} 3{\kern 10pt} 4{\kern 10pt} 5{\kern 10pt}6{\kern 10pt}7{\kern 11pt}8{\kern 10pt}9{\kern 7pt} 10{\kern 6pt} 11{\kern 5pt} 12\\ \left( {\begin{array}{*{20}{l}} 1&1&1&1&2&2&2&2&0&0&0&0\\ 1&0&0&0&2&1&1&1&0&2&2&2\\ 0&1&2&0&1&1&2&0&2&1&2&0 \end{array}} \right) \end{array}$

（3）称重

将正序码第一位为1的硬币放在天平的左侧，为2的放在右侧，为0的放在旁边：

将正序码第二位为1的硬币放在天平的左侧，为2的放在右侧，为0的放在旁边：

将正序码第三位为1的硬币放在天平的左侧，为2的放在右侧，为0的放在旁边：

结果与事先挑选的6号硬币一致
附录

称球通解问题的证明

摘自The Problem of the Pennies, F. J. Dyson, The Mathematical Gazette , Vol. 30, No. 291 (Oct., 1946), pp. 231-234

引理1：在多于2个的一堆球，已知次品在其中，称k次可以并最多在3^k个半确定的球中找出次品，并且知道其轻重。

用数学归纳法，当

$k=1$
。3个半确定的球，一定至少有两个属于同一类，比如说疑重球，将这两个上天平，重的那个就是次品，如果平衡，外边的那个就是次品，而且从它的类别知道这次品是较重还是较轻。验证正确。

假设结论对

$k-1$
次正确。将不多于

$3^k$
个半确定的球三等分，如果不能够等分，除天平两边要等数外，三方都不多于

$3^(k-1)$
个球，且使得两边共有偶数个疑重球，记为

$2a$
个。这总是可以做到的。因为我们可以把天平上“不齐整”的球和外面异类的球对调。这样天平左右各有

$a$
个疑重球和

$3^{k-1}-a$
个疑轻球。这一般有多种可能的

$a$
值满足要求，任取一个都行。这时如果左边重，左边的

$a$
个疑重球和右边的

$3^{k-1}-a$
个疑轻球，共

$3^{k-1}$
个半确定球有嫌疑，其他都是正品。如果右边重，同理将嫌疑缩小到

$3^{k-1}$
个半确定球。如果平衡，嫌疑在外面的

$3^{k-1}$
个半确定球中。如果这嫌疑是1个或2个半确定球，可以用一个正品与其中一个称一次解决，其他情况我们已知用

$k-1$
次可以解决不多于

$3^{k-1}$
个半确定的球。证毕。

引理2：已知次品在其中，加一个已知的正品球称k次，可以并最多在

$\frac{3^{k+1}}{2}$
个球中找出次品，但有且仅有一种情况不知其次品的轻重。

在

$k=1$
情况，有2个球，取一个与正品球上天平，如果平衡，次品在外面，但不知它比正品轻还是重，注意这是归纳证明中仅有的情况。如果只有1个球，它就是次品了，称一次可以知道比正品轻了还是重。

假设结论对

$k-1$
次正确。考虑第一次天平称量，一边取

$\frac{3^{k-1}-1}{2}$
个加上一个正品球，另一边取

$\frac{3^{k-1}-1}{2}$
个球。我们知道这次称量以后，如果天平平衡，那么嫌疑在外面。余下

$k-1$
次可以解决这里的不超过

$\frac{3^{k-1}-1}{2}$
个球，有且仅有一种情况不知其次品的轻重。如果天平不平衡，天平的两边都是半确定的球。由引理1知道，余下

$k-1$
次可以解决这里的

$3^{k-1}$
个球。因为这个数是奇数，所以我们必须在第一次天平称量时再加上一个已知的正品球。因此称

$k$
次，可以并最多解决

$\frac{{{3^{k + 1}}}}{2}$
个球。证毕。

定理：在一堆等重球中有一个重量不同的次品球，用天平称

$k$
次找出来，这堆球最多且可以是

$\frac{3^{k-1}}{2}$
个球。

在第一次称量我们最多可以将

$3^{k-1}-1$
个球两等分放在天平上，如果不平衡，由引理1，可以再称

$k-1$
次解决。如果平衡，天平这里都是已知球，由引理2，可以再称

$k-1$
次解决外面的

$\frac{3^{k-1}+1}{2}$
个球。所以总共可以解决

$\frac{3^{k-1}}{2}$
个球。证毕。

程序代码

package com.yrwan.findCoin;

import java.util.ArrayList;  
import java.util.List;  
import java.util.Scanner;

public class Main {
    static int round = 1;  
    static int maxSteps;  
    public static void run(Status root, List<Status> list) {  //求解 
        List<Status> newlist = new ArrayList<Status>();   
        for (int i=0; i<list.size(); i++) {  
            Status status = list.get(i);  
            status.produceBalances();  
            for (int j=0; j<status.bls.size(); j++) {  
                Balance bl = status.bls.get(j);  
                bl.weight();  
                if (root.succeed()) {  
                    return;  
                }  
                if (bl.out1.isUnknown()) newlist.add(bl.out1);  
                if (bl.out2.isUnknown()) newlist.add(bl.out2);  
                if (bl.out3.isUnknown()) newlist.add(bl.out3);  
            }  
        }  
        round++;  
        run(root, newlist);   
    }  
    public static void print(Status st, int depth) { //输出结果  
        String indent="";  
        for (int i=0; i<depth-1; i++) indent = indent+"t";   
        Balance bl=null;  
        for (int i=0; i<st.bls.size(); i++)   
            if (st.bls.get(i).unresolved==0) bl=st.bls.get(i);  
        if (bl!=null) {  
            if (depth>maxSteps) maxSteps=depth;  
            System.out.println(indent + "第" + depth + "步称重: " + bl + "rn");  
            System.out.println(indent + "如果一样重: " + bl.out1 + (bl.out1.getConclusion()==Status.RESOLVED?"  *解决*":(bl.out1.getConclusion()==Status.REDICULOUS?"  ×不可能×":"")) + "rn");  
            print(bl.out1, depth+1);  
            System.out.println(indent + "如果左边重: " + bl.out2 + (bl.out2.getConclusion()==Status.RESOLVED?"  *解决*":(bl.out2.getConclusion()==Status.REDICULOUS?"  ×不可能×":"")) + "rn");  
            print(bl.out2, depth+1);  
            System.out.println(indent + "如果右边重: " + bl.out3 + (bl.out3.getConclusion()==Status.RESOLVED?"  *解决*":(bl.out3.getConclusion()==Status.REDICULOUS?"  ×不可能×":"")) + "rn");  
            print(bl.out3, depth+1);  
        }  
    }  
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);  
        System.out.println("请输入硬币个数：");  
        int n = sc.nextInt();  
        sc.close();
        Status root = new Status(n);  
        ArrayList<Status> list = new ArrayList<Status>();  
        list.add(root);  
        run(root, list);  
        System.out.println("***** 求解步骤*****");  
        maxSteps = 0;  
        print(root, 1);  
        System.out.println("***** 最少" + maxSteps + "步可找出假币*****");  
    }
}

package com.yrwan.findCoin;

public class Balance {
    public int[] data;  
    public Status in,out1,out2,out3;   
    public int unresolved = 3;  

    public Balance(int[] data) {  
        this.data = data.clone();  
    }  
    public void weight() {//称重量，推理出三种可能的结果   
        int[] temp;  
        // 一样重   
        temp = in.data.clone();  
        for (int i=1; i<4; i++) { //所有参与称重的硬币都移入正常硬币集合   
            temp[0] = temp[0] + data[i] + data[i+4];  
            temp[i] = temp[i] - data[i] - data[i+4];  
        }  
        out1 = new Status(temp);  
        out1.addParent(this);  

        //左边重   
        temp = in.data.clone();  
        for (int i=1; i<4; i++) {  
            temp[0] = temp[0] + temp[i] - data[i] - data[i+4]; //未参与称重的硬币  -->> 正常硬币   
        }  
        temp[0] += data[3] + data[6]; //左边的疑似轻硬币、右边的疑似重硬币  -->> 正常硬币   
        temp[1] = 0;  
        temp[2] = data[1] + data[2]; //左边的不明轻重硬币移入疑似重硬币集合   
        temp[3] = data[5] + data[7]; //右边的不明轻重硬币移入疑似轻硬币集合   
        out2 = new Status(temp);  
        out2.addParent(this);  

        //右边重   
        temp = in.data.clone();  
        for (int i=1; i<4; i++) {  
            temp[0] = temp[0] + temp[i] - data[i] - data[i+4]; //未参与称重的硬币  -->> 正常硬币   
        }  
        temp[0] += data[2] + data[7]; //左边的疑似重硬币、右边的疑似轻硬币  -->> 正常硬币   
        temp[1] = 0;  
        temp[2] = data[5] + data[6]; //右边的不明轻重硬币移入疑似重硬币集合   
        temp[3] = data[1] + data[3]; //左边的不明轻重硬币移入疑似轻硬币集合   
        out3 = new Status(temp);  
        out3.addParent(this);  
    }  
    public String toString(){  
        return "（" + (data[0]>0?"正常硬币×"+data[0]+"个 ":"") + (data[1]>0?"不明硬币×"+data[1]+"个 ":"")   
        +(data[2]>0?"疑似重硬币×"+data[2]+"个 ":"") + (data[3]>0?"疑似轻硬币×"+data[3]+"个 ":"")      
        + "） --天平-- （"  
        + (data[4]>0?"正常硬币×"+data[4]+"个 ":"") + (data[5]>0?"不明硬币×"+data[5]+"个 ":"")   
        +(data[6]>0?"疑似重硬币×"+data[6]+"个 ":"") + (data[7]>0?"疑似轻硬币×"+data[7]+"个 ":"") + "）";     
    }  
    public void prop() {  
        if (unresolved <= 0) return;  
        unresolved--;  
        if (unresolved == 0) in.setConclusion(Status.RESOLVABLE);  
    }  
}

package com.yrwan.findCoin;

import java.util.ArrayList;
import java.util.List;

public class Status {
    public static int RESOLVED=1, UNKNOWN=2, REDICULOUS=3, RESOLVABLE=4;  
    public int count=0;  
    public int[] data;  
    public List<Balance> parents = new ArrayList<Balance>();  
    public List<Balance> bls = new ArrayList<Balance>();  
    private int conclusion;  

    public Status(int c) {  
        count = c;  
        int[] data1 = {0,c,0,0};  
        data = data1;  
        int conc = data[0]<count-1?UNKNOWN:(data[0]==count-1?RESOLVED:REDICULOUS);  
        setConclusion(conc);  
    }  
    public Status(int[] is) {  
        data = is;  
        for (int i=0; i<is.length; i++) count+=is[i];  
        int conc = data[0]<count-1?UNKNOWN:(data[0]==count-1?RESOLVED:REDICULOUS);  
        setConclusion(conc);  
    }  
    public void addParent(Balance bl) {  
        parents.add(bl);  
        if (conclusion==RESOLVED || conclusion==RESOLVABLE || conclusion==REDICULOUS) bl.prop();  
    }  
    public String toString() {  
        return "正常" + data[0] + "、不明" + data[1] + "、或重" + data[2] + "、或轻" + data[3];  
    }  
    public void setConclusion(int conc) {  
        if (conclusion == conc) return;  
        conclusion = conc;  
        if (conclusion==RESOLVED || conclusion==RESOLVABLE || conclusion==REDICULOUS)   
            for (int i=0; i<parents.size(); i++)  
                parents.get(i).prop();  
    }  
    public int getConclusion() {return conclusion;}  
    public boolean succeed() {return conclusion==RESOLVED || conclusion==RESOLVABLE;}  
    public boolean isUnknown(){return conclusion==UNKNOWN;}  

    public void produceBalances() {//得到当前状况下所有可能的称重方案   
        List<int[]> bldata = getBalanceDataArray(data);  
        bls = new ArrayList<Balance>();  
        for (int i=0; i<bldata.size(); i++) {  
            Balance bl = new Balance(bldata.get(i));  
            bl.in = this;  
            bls.add(bl);  
        }  
    }  
    private List<int[]> getBalanceDataArray(int[] src) {  
        List<int[]> list = new ArrayList<int[]>();  
        list.add(new int[src.length*2]);  
        return getBalanceDataArray(src,0,list);  
    }  
    private List<int[]> getBalanceDataArray(int[] src, int id, List<int[]> list) {  
        int total=0,left,right;  
        if (id>=src.length) {  
            for (int i=list.size()-1; i>=0; i--) {  
                int[] is = list.get(i);  
                left=0;  
                right=0;  
                for (int j=0; j<src.length; j++) left+=is[j];  
                for (int j=src.length; j<src.length*2; j++) right+=is[j];  
                if (left!=right || left==0 || is[0]>0&&is[is.length/2]>0)  
                    list.remove(i);  
            }  
            return list;  
        }  
        List<int[]> r = new ArrayList<int[]>();  
        for (int i=0; i<src.length; i++) total += src[i];  
        int half = total/2;  
        for (int i=0; i<list.size(); i++) {  
            int[] is = list.get(i);  
            left=0;  
            right=0;  
            for (int j=0; j<src.length; j++) left+=is[j];  
            for (int j=src.length; j<src.length*2; j++) right+=is[j];  
            for (int j=0; j<=Math.min(half-left, src[id]); j++) {  
                for (int k=0; k<=Math.min(half-right, src[id]-j); k++) {  
                    int[] iis = list.get(i).clone();  
                    iis[id] = j;  
                    iis[id+src.length] = k;  
                    r.add(iis);  
                }  
            }  
        }  
        return getBalanceDataArray(src,id+1,r);  
    }  
}

原文链接：https://blog.csdn.net/yrwan95/article/details/72948905

你可能也喜欢