~~~~
有需求才有供应,很多东西,都是为了解决实际问题才出现的,项目中出现了很多稀疏矩阵,而且需要对他们进行运算,而十字链表就是为了解决稀疏矩阵而出现的一种数据结构。
稀疏矩阵
~~~~
稀疏矩阵(英语:sparse matrix),在数值分析中,是其元素大部分为零的矩阵。反之,如果大部分元素都非零,则这个矩阵是稠密的,通常这个系数被认为是5%。在科学与工程领域中求解线性模型时经常出现大型的稀疏矩阵。
~~~~
在使用计算机存储和操作稀疏矩阵时,经常需要修改标准算法以利用矩阵的稀疏结构。由于其自身的稀疏特性,通过压缩可以大大节省稀疏矩阵的内存代价。更为重要的是,由于过大的尺寸,标准的算法经常无法操作这些稀疏矩阵。
三元组
~~~~
对于矩阵,我们第一想法就是使用二维数组来存储,但是稀疏矩阵的元素大部分都是零,而且稀疏矩阵的尺寸一般都比较大,这个时候我们如果直接使用二维数组,会浪费很多的空间,所有通常我们需要对稀疏矩阵进行压缩,三元组就是一种稀疏矩阵压缩保存的方法。
~~~~
三元组是指形如
(
(
x
,
y
)
,
z
)
((x,y),z)
(
(
x
,
y
)
,
z
)
的集合(这就是说,三元组是这样的偶,其第一个射影亦是一个偶),常简记为
(
x
,
y
,
z
)
(x,y,z)
(
x
,
y
,
z
)
。
~~~~
三元组是计算机专业的一门公共基础课程——数据结构里的概念。主要是用来存储稀疏矩阵的一种压缩方式,也叫三元组表。
~~~~
三元组有不同的实现方法,假设以顺序表存储结构来表示三元组,称为三元组顺序表。
结构如下
#defube NAXSIZE 2500
typedef struct{
int i, j; //该非零元的行下标和列下标
ElemType e;
}Triple;
typedef struct{
Triple data[MAXSIZE + 1];//非零三元数组标,data[0]没有使用
int mu, nu, tu;//矩阵的行数,列数,非零元个数
}TSMatrix;
~~~~
注意,data域中表示非零元的三元组是以行序为主序顺序排列的,如果不排序,你会发现你操作和访问数据时,时间基本都花在查询数据上了。对于三元组,我们可以进行一些运算,都是很容易实现的,比如转置,相加,相减。
~~~~
三元组相比十字链表的缺点(暂时只能想到这些)
- 1、增加或减少矩阵中的非零元素,都需要进行数据的移动
- 2、大小固定,非零数据很少时,会浪费很多的空间,过多时无法保存
- 3、查找元素比较慢(时间复杂度)
- 4、矩阵的运算数据较慢(时间复杂度)
十字链表
~~~~
十字链表(英语:Orthogonal linked list)是计算机科学中的一种高级数据结构,在Linux内核中应用广泛。具体说,一个二维十字链表是链表的元素同时链接左右水平邻结点与上下垂直邻结点。
~~~~
当稀疏矩阵的非零元个数和位置在操作过程中变化较大时,就不宜使用顺序表存储结构的三元组来保存稀疏矩阵;这个时候我们采用的时十字链表。
十字链表节点结构
typedef struct OLNode {
int LineNumber, ColumneNumber; //行号与列号
ElemType value; //值
struct OLNode *right, *down; //同行、同列下一个元素的指针
}OLNode, *OList;
typedef struct{
OList *rhead, *chead; //行和列链表头指针向量基址
int mu,nu,tu; //稀疏矩阵的行数,列数和非零元个数
}CrossList;
~~~~
每一个非零元可用一个含5个域的节点表示,其中i,j和e这3个域分别表示该非零元所在的行、列和非零元的值,向右域right用以链接同一行中下一个非零元,向下域down用来链接同一列下一个非零元,同一行的非零元通过right链接形成一个线性链表,同一列的非零元通过down链接形成一个线性表,每个非零元既是某个行链表中的节点,也是某一个列链表中的节点,整个矩阵构成了一个十字交叉的链表,而样的链表存储结构称为十字链表。
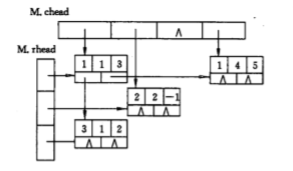
附上十字链表实现(百度抄的)
#include <malloc.h>
#include <stdio.h>
/*十字链表的结构类型定义如下:*/
typedef struct OLNode
{
int row,col; /*非零元素的行和列下标*/
int value;
struct OLNode *right; /*非零元素所在行表、列表的后继链域*/
struct OLNode *down;
} OLNode, *OLink;
typedef struct
{
OLink *row_head; /*行、列链表的头指针向量*/
OLink *col_head;
int m,n,len; /*稀疏矩阵的行数、列数、非零元素的个数*/
} CrossList;
/*建立稀疏矩阵的十字链表的算法*/
void CreateCrossList(CrossList *M)
{
int m, n, t, i, j, e;
OLNode* p;
OLNode* q;
/*采用十字链表存储结构,创建稀疏矩阵M*/
scanf("%d%d%d", &m,&n,&t); /*输入M的行数,列数和非零元素的个数*/
M->m=m;
M->n=n;
M->len=t;
if(!(M->row_head=(OLink *)malloc(m*sizeof(OLink))))
exit(OVERFLOW);
if(!(M->col_head=(OLink * )malloc(n*sizeof(OLink))))
exit(OVERFLOW);
/*初始化行、列,头指针指向量,各行、列链表为空的链表*/
for(int h=0; h<m+1; h++)
{
M->row_head[h] = NULL;
}
for(int t=0; t<n+1; t++)
{
M->col_head[t] = NULL;
}
for(
scanf("%d%d%d", &i,&j,&e); e!=0; scanf("%d%d%d", &i,&j,&e))
{
if(!(p=(OLNode *)malloc(sizeof(OLNode))))
exit(
OVERFLOW);
p->row=i;
p->col=j;
p->value=e; /*生成结点*/
if(M->row_head[i]==NULL)
M->row_head[i]=p;
p->right=NULL;
else
{
/*寻找行表中的插入位置*/
for(q=M->row_head[i]; q->right&&q->right->col<j; q=q->right); /*空循环体*/
p->right=q->right;
q->right=p; /*完成插入*/
}
if(M->col_head[j]==NULL)
M->col_head[j]=p;
p->down=NULL;
else
{
/*寻找列表中的插入位置*/
for(q=M->col_head[j]; q->down&&q->down->row<i; q=q->down); /*空循环体*/
p->down=q->down;
q->down=p; /*完成插入*/
}
}
}