博客

卷积、傅里叶级数、傅里叶变换、快速傅里叶变换、pytorch中的fft，rfft

  • Post author:
  • Post category:其他


卷积：

连续形式：

(f*g)(n) = \ \int_{\propto }^{\propto }f(\tau )g(n-\tau )d\tau

离散形式：

(f*g)(n) = \sum_{-\propto }^{\propto }f(\tau )g(n-\tau )


‘卷’

：  翻转 和 滑动

‘积‘

： 积分

翻转：g(t)  – >  g(-t)

滑动：g(-t) – > g(n-t) 平移n个单位


举个例子

：信号分析 (摘自

(6 封私信 / 10 条消息) 如何通俗易懂地解释卷积？ – 知乎 (zhihu.com)

)

f(t) ：输入的信号

g(t)：为衰减函数 ，在0时刻的信号，经过T时刻以后，衰减为f(0)g(T)

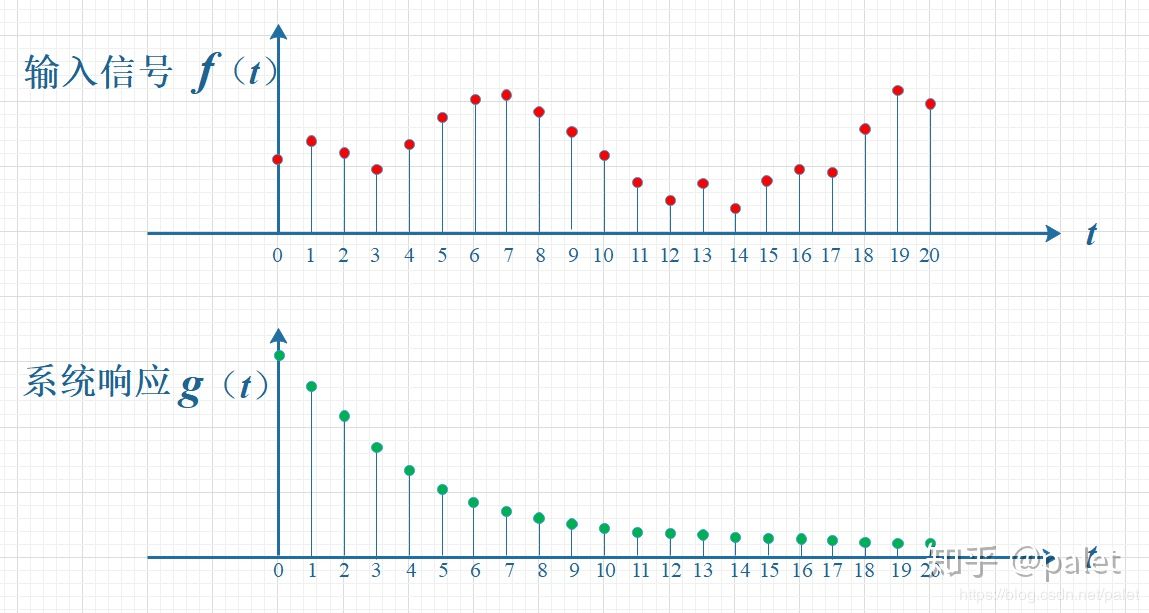
因为考虑到T时刻的输出信号，会受到前面0，1，，，T-1时刻的所有信号的影响，所以必须将起那面T个时刻的衰减后的信号进行叠加，得到T时刻的信号值。下图为叠加过程。

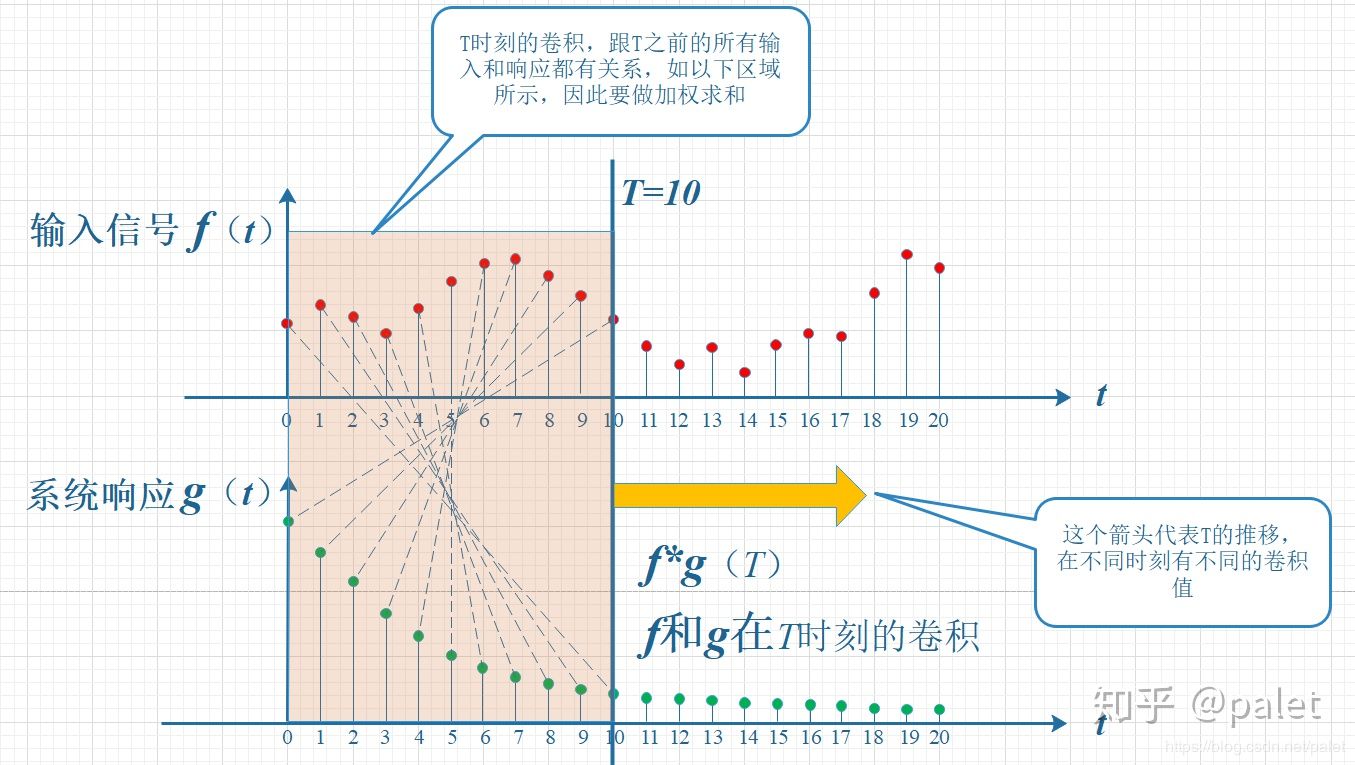
经过翻转：

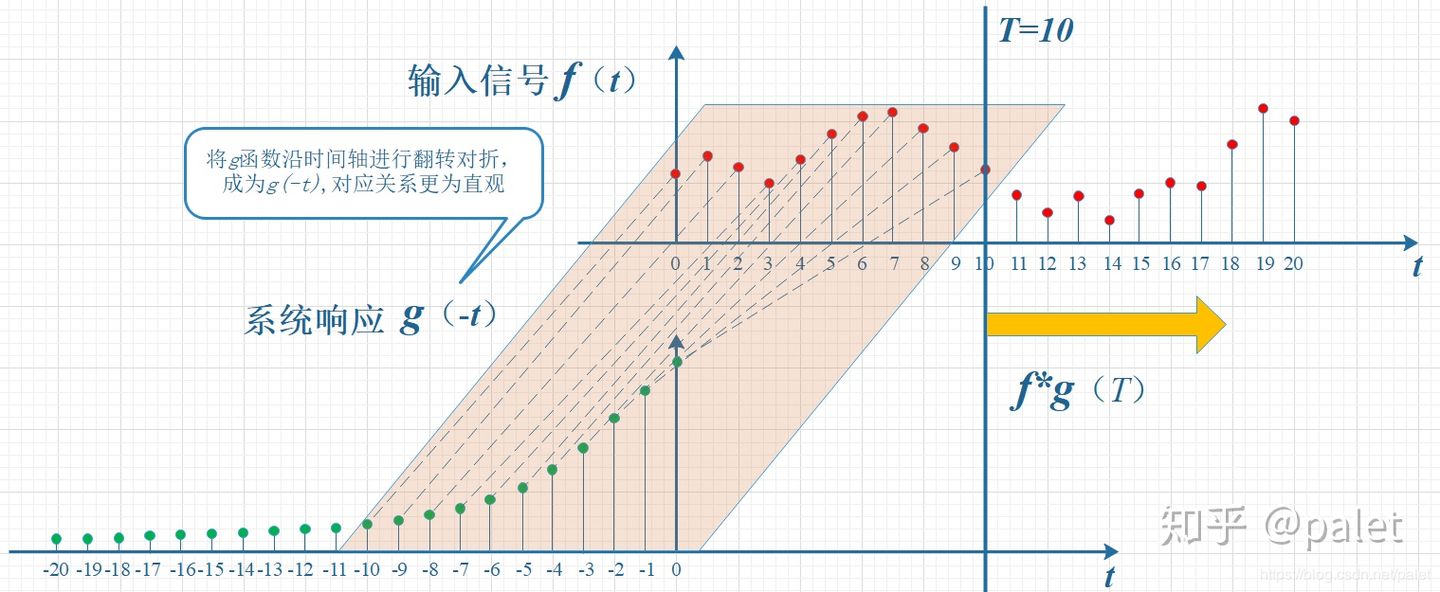
经过平移滑动：

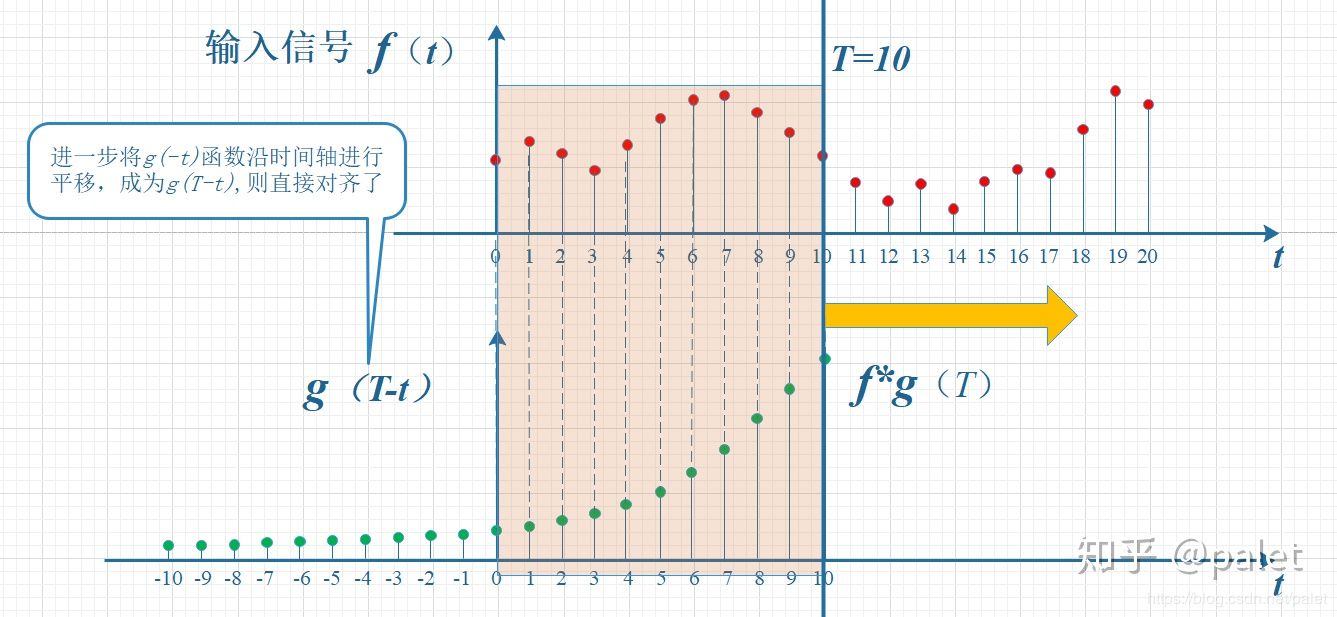
二维卷积：

(f*g)(u,v) = \sum_{i}^{}\sum_{j}^{}f(i,j)g(u-i,v-j)

傅里叶级数：

三角函数系（正交）：{1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…}

\int_{-\pi }^{\pi }f(x)g(x)dx = 0 (f(x) \neq g(x) )

\int_{-\pi }^{\pi }f(x)^{2}dx = \pi (f(x)\neq 1)

周期为2
\pi
的函数傅里叶展开：
f(x) = \sum_{n=0}^{\propto }a_{n}cosnx + \sum_{n=0}^{\propto }b_{n}sinnx

a_{0} = \frac{1}{2\pi }\int_{-\pi }^{\pi }f(x)dx\ , a_{n} = \frac{1}{\pi }\int_{-\pi }^{\pi }f(x)cosnxdx\ , b_{n} = \frac{1}{\pi }\int_{-\pi }^{\pi }f(x)sinnxdx

周期为2
l
的函数傅里叶展开:
f(x) = \sum_{n=0}^{\propto }a_{n}cos\frac{n\pi x}{l} + \sum_{n=0}^{\propto }b_{n}sin\frac{n\pi x}{l}

a_{0} = \frac{1}{2l}\int_{-l }^{l}f(x)dx\ , a_{n} = \frac{1}{l }\int_{-l }^{l }f(x)cos\frac{n\pi x}{l}dx\ , b_{n} = \frac{1}{l}\int_{-l }^{l }f(x)sin\frac{n\pi x}{l}dx

傅里叶变换：

连续傅里叶变换：
F(w) = \int_{-\propto }^{\propto }x(t)e^{-jwt}dt

连续逆傅里叶变换：
f(t) = \frac{1}{2\pi }\int_{-\propto }^{\propto }F(w)e^{jwt}dw

离散傅里叶变换：
F(u) = \sum_{x=0}^{M-1}f(x)e^{-j\frac{2\pi ux}{M}}

离散逆傅里叶变换：
f(x) = \frac{1}{M}\sum_{u = 0}^{M-1}F(u)e^{j\frac{2\pi ux}{M}}

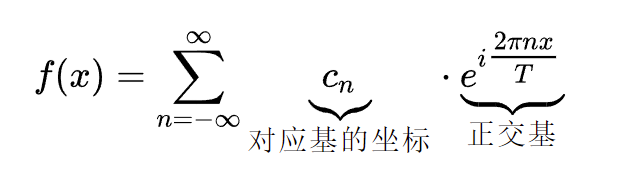
傅里叶级数写为欧拉公式格式：
f(x) = \sum_{n = -\propto }^{\propto } c_{n}e^{j\frac{2\pi nx}{T}}
其中
c_{n} = \frac{1}{T}\int_{x_{0}}^{x_{o}+T}f(x)e^{-j\frac{2\pi nx}{T}}dx


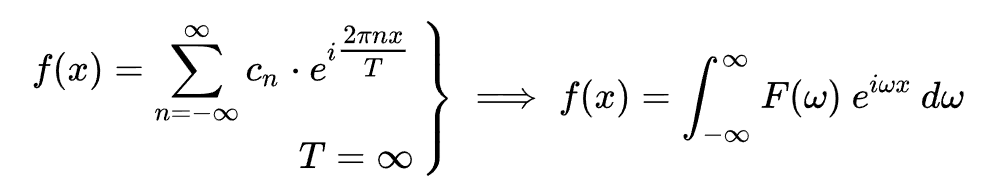
借鉴：

(6 封私信 / 12 条消息) 傅里叶级数和傅里叶变换是什么关系？ – 知乎 (zhihu.com)

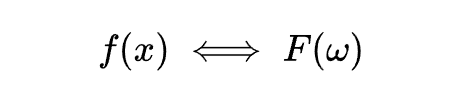
实质：傅里叶变换就是为了求傅里叶级数中的
a_{n},b_{n}
, 这个就是频率，只不过将sinnx和cosnx合在一起写了 (欧拉公式：
(e^{jx} = cosx + jsinx)
）。

快速傅里叶变换：

快速傅里叶变换提出主要的目的是为了解决将多项式的系数表达形式转换为点值表达式。

两种表达式可以参考：

(6条消息) 十分简明易懂的FFT（快速傅里叶变换）_路人黑的纸巾-CSDN博客_fft


下面的n定义为2的次幂

n次单位根：
w_{n}^{1}
(w_{n}^{1})^{k} = w_{n}^{k}
w_{n}^{k} = cos\frac{k}{n}2\pi + j sin\frac{k}{n}2\pi
w_{n}^{0} = w_{n}^{n} =1

w_{k}^{n} = w_{2n}^{2k}
w_{n}^{k + \frac{n}{2}} = -w_{n}^{k}

另
A(x) = \sum_{i=0}^{n-1} a_{i}x^{i}
A(x) = (a_{0} + a_{2}x^{2}+\cdots +a_{n-2}x^{n-2}) + x(a_{1} + a_{3}x^{2}+\cdots +a_{n-1}x^{n-2})

另
A_{1}(x) = a_{0} + a_{2}x^{2}+\cdots +a_{n-2}x^{n-2}\\ A_{2}(x) = a_{1} + a_{3}x^{2}+\cdots +a_{n-1}x^{n-2}

所以
A(w_{n}^{k})
和
A(w_{n}^{k+\frac{n}{2}})
可以同时求出来，利用递归的思想可以得到lnn的计算复杂度。分而治之


傅里叶变换的共轭对称性：(摘自


(6条消息) 共轭复数，共轭根式，共轭矩阵，共轭方向，共轭方向法，共轭梯度法，共轭分布，共轭函数，傅里叶变换的共轭对称_Strive_For_Future的博客-CSDN博客_共轭复数的傅里叶变换


)

可以得到一维：
F(u) = F^{*}(-u)
二维：
F(u,v) = F^{*}(-u,-v)
这里的u，v都是坐标点位置值

摘自：

(6条消息) 傅里叶变换(二维离散傅里叶变换)_thecentury的博客-CSDN博客_二维傅里叶变换

一维下：

相同颜色的w计算的频率是共轭的。

二维下：F(u,v)


中心共轭对称

（相同颜色的值互为共轭）（除去0行0列，剩下的中心共轭对称，0行0列各自也共轭对称）图中相同颜色的是共轭对称的。

摘自：(

(6 封私信 / 14 条消息) 二维傅里叶变换是怎么进行的？ – 知乎 (zhihu.com)

)

在利用快速傅里叶变换做傅里叶变换时，应该选取几个坐标基？pytorch中会选取与原时间域相同个数的基。例如：在离散傅里叶变换时，我们有8个f(x)的值，则会选取8次单位根的8个w作为基。

pytorch中 fft、rfft的不同？：

fft：快速离散傅里叶变换

rfft：因为中心共轭对称，所以将共轭的那一部分去除，减少存储量

带有r的，其意义都是去除那些共轭对称的值，减小存储


版权声明：本文为qq_44901773原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。